-
摘要: 针对交通流模型的多样性和同一参数测量值的变化, 分析了建模思想和测量统计方法一致性的必要。根据模型参数的物理意义, 通过量纲分析方法, 对各种交通流模型及其参数进行研究, 从中得到各个模型之间本质上具有相似性的基本结论, 以及主要无量纲参数之间的函数关系式。对交通流局部密度增大后消散问题从无量纲入手, 得到的无量纲结论能够说明有量纲低速和高速交通流模型问题。此示例说明量纲分析方法对交通流模型及其参数研究具有理论和实际应用价值。Abstract: According to the multiformity of traffic flow models and the measure value variety of the same parameter, this paper analysed the modeling principles and the consistent of measure and statistics methods. In the light of the physical magnificence of model parameters, applying the dimension analysis method, the paper studied several traffic flow models and their parameters, and deduced the basic results about the similarity of these models and the function formulas of their parameters. The dissipation procedure of traffic flow density wave was analyzed by dimensionless theory, and the analytic conclusion can explain the dimensional counterpart of high velocity and low velocity traffic flow models. The dimension analysis method has theoretical and practical value for further developing traffic flow theories.
-
表 1 交通流模型参数
Table 1. Parameters of traffic flow model
参数 模型 Cremer (高速) 姜紫峰(高速) Payne (城市) 吴正(城市) 冯苏苇(城市) L/m 2 000 2 000 1 000 500 500 T/s 60 70 75 70 60 q0/ (veh·s-1) 1.80 0.90 0.40 0.30 0.25 uf/ (m·s-1) 34.17 28.33 13.42 7.00 8.72 ρjam/ (veh·m-1) 0.200 0.116 0.109 0.150 0.112 ρcr/ (veh·m-1) / 0.029 0 / 0.073 5 0.075 0 Tr/s 36.00 15.84 0.75 / 7.00 C0/ (m·s-1) 12.90 27.78 15.48 6.30 21.30 
下载: 导出CSV
表 2 无量纲参数
Table 2. Dimensionless parameters
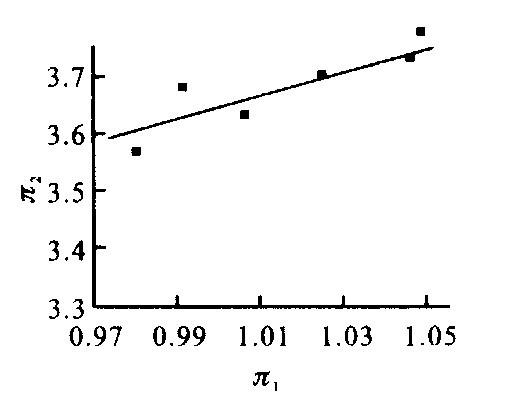
参数 模型 Cremer (高速) 姜紫峰(高速) Payne (城市) 吴正(城市) 冯苏苇(城市) π1 1.025 1 0.991 6 1.006 5 0.980 0 1.046 4 π2 3.703 7 3.682 5 3.633 3 3.571 4 3.733 3 π3 / 0.920 6 / 1.750 0 2.500 0 π4 0.600 0 0.226 3 0.010 0 / 0.116 7 π5 0.387 0 0.972 3 1.161 0 0.882 0 2.556 0
下载: 导出CSV
-
[1] Whitham G B. Linear and Nonlinear Waves[M]. New York: John Wiley and Sons Inc., 1974. [2] Payne H J. Models of freeway traffic and control[J]. Simulation Council Preceding Series, 1971, 1(1): 51-61. [3] 冯苏苇. 低速混合型城市交通流的建模[D]. 上海: 上海大学, 1997. [4] 吴正. 交通流的动力学模拟与测量方法[J]. 复旦学报(自然科学版), 1991, 30(1): 111-117. https://www.cnki.com.cn/Article/CJFDTOTAL-FDXB199101017.htmWU Zheng. Dynamics simulation and investigation method of traffic flow[J]. Journal of Fudan University(Natural Science), 1991, 30(1): 111-117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FDXB199101017.htm [5] 吴正. 低速混合型城市交通的流体力学模型[J]. 力学学报, 1994, 26(2): 149-157. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB402.002.htmWU Zheng. A fluid dynamics model for the low velocity traffic systems[J]. ACTA Mechanica Sinica, 1994, 26(2): 149-157. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB402.002.htm [6] 王明祺. 交通流理论的研究进展[J]. 力学进展, 1995, 25(3): 343-356. doi: 10.3321/j.issn:1000-0992.1995.03.008WANG Ming-qi. Advances of the research on traffic flow theory[J]. Advances in Mechanics, 1995, 25(3): 343-356. (in Chinese) doi: 10.3321/j.issn:1000-0992.1995.03.008 [7] 戴世强. 交通流动力学[J]. 自然杂志, 1996, 19(4): 196-201. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZZ199704002.htmDAI Shi-qiang. Traffic flow dynamics[J]. Journal of Nature, 1996, 19(4): 196-201. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZZ199704002.htm [8] 宫晓燕. 高速公路交通流建模综述[J]. 交通运输工程学报, 2002, 2(1): 74-79. http://transport.chd.edu.cn/article/id/200201016GONG Xiao-yan. Survey on freeway traffic flow modeling[J]. Journal of Traffic and Transportation Engineering, 2002, 2(1): 74-79. (in Chinese) http://transport.chd.edu.cn/article/id/200201016 [9] 吴正, 汪茂林. 高速公路交通流事故和干涉车流波的非线性数学模型[J]. 西安公路交通大学学报, 2001, 21(2): 77-80. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200102025.htmWU Zheng, WANG Mao-lin. On the nonlinear modeling for expressway incident and intervention traffic flow wave[J]. Journal of Xi' an Highway University, 2001, 21(2): 77-80. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200102025.htm -
点击查看大图
图(6) / 表(2)
计量
- 文章访问数: 317
- HTML全文浏览量: 187
- PDF下载量: 542
- 被引次数: 0
