信号交叉口行人过街时间模型

徐良杰; 王炜

信号交叉口行人过街时间模型

徐良杰^1,,
王炜¹

1.
东南大学交通学院, 江苏南京 210096
2.
武汉科技大学交通运输系, 湖北武汉 430070

基金项目:

国家自然科学基金项目 50378016

详细信息

作者简介:
徐良杰(1968-), 女, 湖北武汉人, 东南大学博士研究生, 从事交通信息工程及控制研究

中图分类号: U491.51
计量
- 文章访问数: 291
- HTML全文浏览量: 91
- PDF下载量: 246
- 被引次数: 0
出版历程
- 收稿日期: 2004-12-14
- 刊出日期: 2005-03-25

Model of pedestrians crossing time at signalized intersection

XU Liang-jie^1
,,
WANG Wei¹

1.
School of Transportation, Southeast University, Nanjing 210096, China
2.
Department of Transportation, Wuhan University of Science and Technology, Wuhan 430070, China

More Information

Author Bio:
XU Liang-jie(1968-), female, doctoral student, 86-27-87385185, laurie119@sina.com

摘要

摘要: 为了分析交叉口处左转及右转机动车对行人过街交通的干扰和影响, 合理控制交叉口行人过街信号, 应用交通流冲突理论、间隙接受理论, 推导了行人穿越机动车道的人数及等待通行人数, 应用统计学方法, 建立了行人过街时间模型。实例分析表明, 行人平均过街时间的绝对误差及相对误差平均值分别为0.452 7 s和4.15%, 85%行人过街时间的绝对误差及相对误差平均值分别为0.206 5 s和1.57%, 90%行人过街时间的绝对误差及相对误差平均值分别为0.401 2 s和2 84%, 模型计算精度满足要求, 有利于行人专用信号相位的设置。
- 交通控制 /
- 信号交叉口 /
- 行人过街时间 /
- 冲突 /
- 穿越间隙 /
- 车头时距
Abstract: In order to analyze the influence of turning vehicles on pedestrians crossing time, and to provide rational pedestrians control signal, the pedestrians number of crossing and waiting-crossing crosswalk were calculated, by using the conflict theory and the critical-gap accepted theory the models of pedestrians crossing time were built up. The absolute error and relative error of pedestrians crossing average time, are respectively 0.452 7 s and 4.15%, the absolute error and relative error of 85% pedestrians crossing average time are respectively 0.206 5 s and 1.57%; the absolute error and relative error of 90% pedestrians crossing average time are respectively 0.401 2 s and 2.84%. Computation results show that the precision of the models is high, the models are feasible for the pedestrians phase setting at signalized intersection.
- traffic control /
- signalized intersection /
- pedestrians crossing time /
- conflict /
- crossing gap /
- headway

HTML全文

图 1 临界穿越间隙值图解法

Figure 1. Schematic diagram of critical gap

下载: 全尺寸图片幻灯片

图 2 穿越转向机动车流的行人人数估算

Figure 2. Estimating value of pedestrians crossing turning vehicle flow

下载: 全尺寸图片幻灯片

图 3 双向两车道转向机动车对行人影响

Figure 3. Fig.3 Effect of turning vehicles on pedestrians attwo lanes intersection

下载: 全尺寸图片幻灯片

图 4 双向四车道转向机动车对行人影响

Figure 4. Fig.4 Effect of turning vehicles on pedestriansat four lanes intersection

下载: 全尺寸图片幻灯片

图 5 人行横道长度对行人过街时间误差影响

Figure 5. Effect of crossing width on crossing time

下载: 全尺寸图片幻灯片

图 6 机动车流量对行人过街时间误差影响

Figure 6. Effect of vehicle volume on crossing time

下载: 全尺寸图片幻灯片

图 7 路口车道数与行人过街时间关系

Figure 7. Relationship between lanes and crossing time

下载: 全尺寸图片幻灯片

图 8 车头时距分布对行人过街时间误差影响

Figure 8. Effect of headway distribution on crossing time

下载: 全尺寸图片幻灯片

表 1 车头时距分布选择方法

Table 1. Choice methods of headway distribution

信号相位饱和度C_s	车辆到达规律	车头时距分布f (t_hd)
0.5~0.6	Poisson随机到达	负指数分布
0.6~0.7	非拥挤状况下的自由交通流	对数正态分布、PearsonⅢ型分布和Erlang分布
0.7~0.8	自由流和非自由流	移位负指数分布、对数正态分布
0.8~0.9	拥挤状况下的非自由流	移位负指数分布、对数正态分布

下载: 导出CSV

表 2 穿越间隙观测值

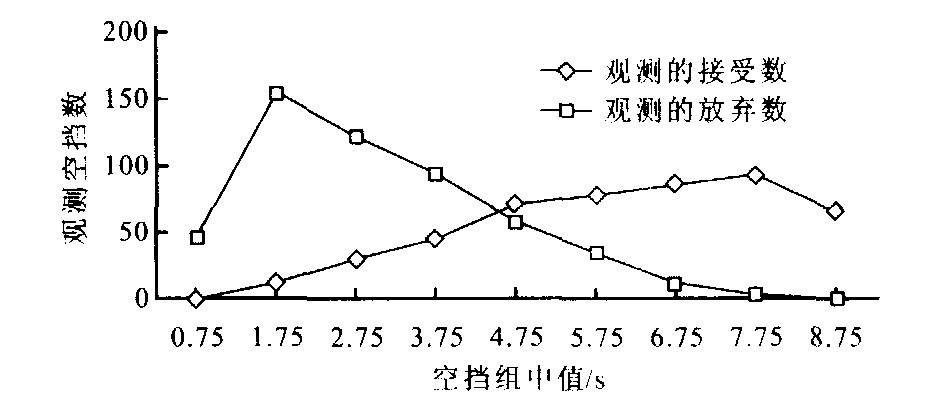
Table 2. Survey data of crossing gap

1	2	3	4
穿越间隙时间分组/s	放弃的观测数	接受的观测数	观测的接受百分比
0.25~1.25	46	0	0
1.25~2.25	153	11	7
2.25~3.25	122	29	19
3.25~4.25	94	44	32
4.25~5.25	58	71	55
5.25~6.25	35	78	69
6.25~7.25	11	86	89
7.25~8.25	3	93	97
8.25~9.25	0	66	100

下载: 导出CSV

参考文献(6)

[1]	刘小明, 段海林. 平面交叉口交通冲突技术标准化研究[J]. 公路交通科技, 1997, 17(3): 49-53. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK703.005.htm LIU Xiao-ming, DUAN Hai-lin. Research on standard program of traffic conflict techniques at intersections[J]. Journal of Highway and Transportation Research and Development, 1997, 17(3): 49-53. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK703.005.htm
[2]	徐立群, 吴聪, 杨兆升. 信号交叉口通行能力计算方法[J]. 交通运输工程学报, 2001, 1(1): 82-85. http://transport.chd.edu.cn/article/id/200101021 XU Li-qun, WU Cong, YANG Zhao-sheng. The methods of computing the capacity of signalized intersection[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 82-85. (in Chinese) http://transport.chd.edu.cn/article/id/200101021
[3]	黄文忠, 杨佩昆. 无控制人行横道处的行人和机动车延误分析[J]. 同济大学学报, 1995, 23(1): 31-36. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ501.007.htm HUANG Wen-zhong, YANG Pei-kun. Delays of pedestrians and vehicles at the nonsignalized zebra crossing[J]. Journal of Tongji University, 1995, 23(1): 31-36. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ501.007.htm
[4]	马万经, 林瑜, 杨晓光. 多相位信号控制交叉口行人相位设置方法[J]. 交通运输工程学报, 2004, 4(2): 103-106. http://transport.chd.edu.cn/article/id/200402024 MA Wan-jing, LIN Yu, YANG Xiao-guang. Design method of pedestrian phases at multi-phase signal intersection[J]. Journal of Traffic and Transportation Engineering, 2004, 4(2): 103-106. (in Chinese) http://transport.chd.edu.cn/article/id/200402024
[5]	高海军, 陈龙, 石松泉. 交通路口混合交通流的分布式模糊控制[J]. 中国公路学报, 2003, 16(4): 67-71. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200304015.htm GAO Hai-jun, CHEN Long, SHI Song-quan. Distributed fuzzy control under hybrid traffic flow of a traffic intersection[J]. China Journal of Highway and Transport, 2003, 16(4): 67-71. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200304015.htm
[6]	徐珺, 皱智军, 杨锦冬. 中小城市道路平交交通设计[J]. 长安大学学报(自然科学版), 2003, 23(4): 58-61. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200304015.htm XU Jun, ZOU Zhi-jun, YANG Jin-dong. At-grade intersection design in medium or small urban[J]. Journal of Chang'an University(Natural Science Edition), 2003, 23(4): 58-61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200304015.htm