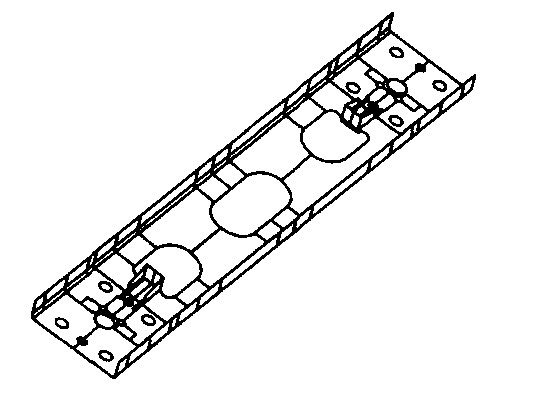
Spring plank stiffness influence of swing bogie freight car on its dynamics performances
-
摘要: 为分析弹簧托板的形式对摆动式转向架货车动力学性能的影响, 利用有限单元法将弹簧托板等效为一根弹性梁, 根据Hook定律得到弹簧托板与摇动台的连接刚度, 通过改变弹簧托板的半径, 得到不同半径下弹簧托板与摇动座的连接刚度。运用多体系统动力学原理, 考虑车辆各个部件的连接和接触关系, 建立整个车辆的多体系统动力学模型, 通过对比不同弹簧托板半径下车辆的各主要动力学性能指标, 得到较为合适的弹簧托板半径。综合对比不同弹簧托板半径下的车辆动力学分析结果得出, 随着弹簧托板半径的增大, 车辆的临界速度减小, 车体横向平稳性增加, 而车辆的运行稳定性指标出现波动, 当弹簧托板半径为10m时, 车辆的各主要动力学性能较好, 其对车辆的动力学性能影响较小。Abstract: In order to analyze the effect of spring plank stiffness on the dynamics performances of swing bogie freight car, the spring plank was considered as an elastic beam using finite element method. According to Hook law, the displacement stiffness and rotation stiffness were gotten when spring plank was connected with swing bolsters, different connection stiffness values were obtained by changing spring plank radius. The multi-body system dynamics model of global vehicle was established by multi-body system dynamics theory, based on taking into account each component connection and contact relation of vehicle. Rational radius of spring plank was presented by comparing with the main dynamics performances of vehicle under different spring plank radii. Analysis results indicate that along with the increase of spring plank radius, the critical velocity of vehicle decreases, the lateral riding index of car body increases, and the running stability indices fluctuate, each main dynamics performance of vehicle is better when spring plank radius is 10 m.
-
图 4 货车的半车多体系统拓扑结构
Figure 4. Multi-body system topology structure of half of freight car
表 1 不同半径弹簧托板的等效刚度
Table 1. Equivalent stiffnesses of different spring plank radii
半径/m Kx/(N·m-1) Ky/(N·m-1) Kz/(N·m-1) Kα/(Nm·rad-1) Kβ/(Nm·rad-1) Kγ/(Nm·rad-1) ∞ 1.57×107 5.06×108 8.70×105 7.04×106 1.40×104 9.09×107 25 7.35×106 4.93×108 8.70×105 7.04×106 1.40×104 8.77×107 20 6.13×106 4.83×108 8.70×105 7.04×106 1.40×104 8.70×107 15 4.67×106 4.63×108 8.70×105 7.04×106 1.40×104 8.55×107 10 2.91×106 4.08×108 8.70×105 7.04×106 1.40×104 8.33×107 5 1.04×106 2.42×108 8.70×105 7.04×106 1.41×104 8.06×107 
下载: 导出CSV
-
[1] Wang Yong, Zeng Jing, Lu Ke-wei. Dynamics modeling and simulation of three-piece bogie freight car[J]. Journal of Traffic and Transportation Engineering, 2003, 3(4): 30-34. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201905015.htm [2] 严隽耄. 车辆工程[M]. 北京: 中国铁道出版社, 1999. [3] 雷晓燕. 有限元法[M]. 北京: 中国铁道出版社, 2000. [4] 洪嘉振. 计算多体系统动力学[M]. 北京: 高等教育出版社, 1999. [5] 孙世基, 黄承绪. 机械系统刚柔耦合动力分析及仿真[M]. 北京: 人民交通出版社, 2000. [6] Gerl J, Kaprolat H, Mauer L. The manchester benchmarks SI- MPACK statement of method[J]. Vehicle System Dynamics, 1999, 31(Sup): 78-84. https://www.cnki.com.cn/Article/CJFDTOTAL-STYS202010013.htm [7] Schupp G, Netter H, Mauer L, et al. Multibody system simulation of railway vehicles with SIMPACK[J]. Vehicle System Dynamics, 1999, 31(Sup): 101-118. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201413011.htm [8] Netter H, Schupp G, Rulka W, et al. New aspects of contact modeling and validation within multibody system simulation of railway vehicles[J]. Vehicle System Dynamics, 1998, 28(Sup): 246-269. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201413011.htm [9] 王福天. 车辆系统动力学[M]. 北京: 中国铁道出版社, 1996. 18交通运输工程学报2005年 -
点击查看大图
图(10) / 表(1)
计量
- 文章访问数: 292
- HTML全文浏览量: 93
- PDF下载量: 239
- 被引次数: 0
