Vertical vibration isolation and suspension parameter optimization of railway vehicle
-
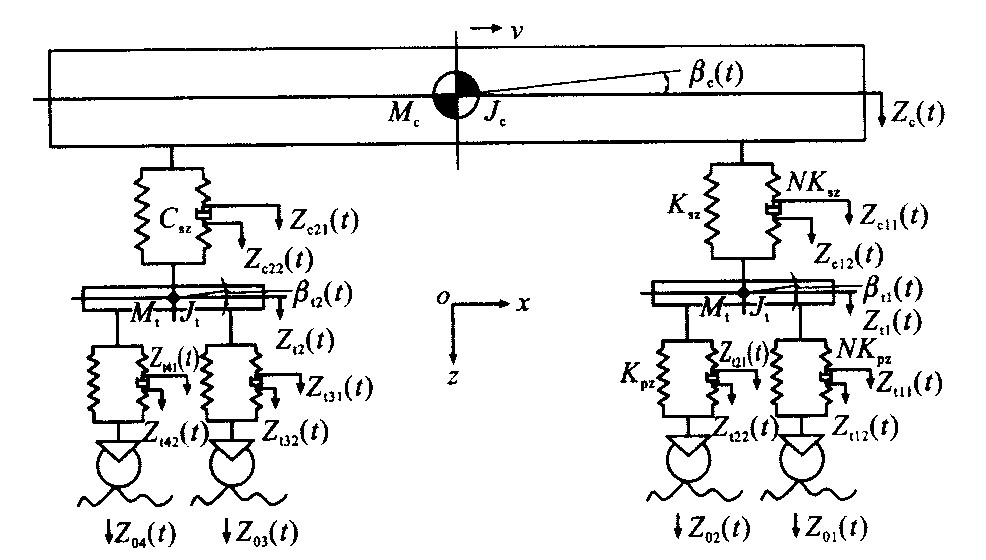
摘要: 为了优化铁道客车垂向悬挂系统参数的选取, 建立了铁道客车垂向悬挂系统广义鲁茨卡(Ruzicka)隔振模型, 研究其简谐隔振特性, 应用评价函数法, 对铁道客车垂向悬挂系统进行多目标、多参数优化, 以使车体的垂向振动位移和加速度最小。分析比较优化后的结果可知, 多目标优化结果明显优于单目标优化结果, 悬挂参数的取值和优化目标有很大的关系, 不同的优化目标会得到不同的优化结果。Abstract: In order to provide a new and efficient method for the selection of vertical suspension parameters of railway passenger car, an extended Ruzicka vibration isolation model of the vertical suspension system was set up, and the harmonic vibration isolation properties of the system were investigated, the optimization method of multiple aims and multiple parameters for the system was carried out by evaluation function method so that the minimum vertical displacement and acceleration of carbody could be obtained. Numerical computation result indicates that the values of optimized result with multi-aim method are much better than the values with single-aim method, the final optimized parameters are related with the optimization aims, and different optimization results are achieved with different optimization aims.
-
表 1 系统参数取值
Table 1. Parameters values of vehicle system
名称 Mc/t Jc/(t·m2) Mt/t Jt/(t·m2) 2L/m 2Lt/m 取值 33.6 2 040 3.6 4.15 18.0 2.4 
下载: 导出CSV
表 3 优化参数取值区间
Table 3. Parameter selection ranges
Kpz/(MN·m-1) Ksz/(MN·m-1) Cpz/(kN·s·m-1) Csz/(kN·s·m-1) NKpz/(MN·m-1) NKsz/(MN·m-1) 下限 0.5 0.2 10 20 0.5 0.5 上限 1.5 0.5 60 100 2.5 2.5
下载: 导出CSV
表 4 参数优化结果
Table 4. Optimized parameter values
名称 Kpz/(MN·m-1) Ksz/(MN·m-1) Cpz/(kN·s·m-1) Csz/(kN·s·m-1) NKpz/(MN·m-1) NKsz/(MN·m-1) 优化前 0.70 0.35 30.0 40.0 1.5 0.75 优化后 第1组 0.50 0.20 60.0 100.0 1.6 2.50 第2组 0.50 0.20 18.7 20.0 2.5 0.50 第3组 0.50 0.20 38.0 20.2 2.5 2.50
下载: 导出CSV
-
[1] 王福天. 车辆系统动力学[M]. 北京: 中国铁道出版社, 1993. [2] Garg V K, Dukkipati R V. Dynamics of Vehicle System Dynamics[M]. Toronto: Academic Press, 1984. [3] 丁文镜. 减振理论[M]. 北京: 清华大学出版社, 1988. [4] Alkhatib R, Nakhaie J G, Golnaraghi M F. Optimal design of passive linear suspension using genetic algorithm[J]. Journal of Sound and Vibration, 2004, 275(5): 665—691. [5] 陈先进, 齐欢, 吴崇健, 等. 基于极大熵法的两级隔振系统的优化设计[J]. 振动与冲击, 1999, 18(4): 45—49. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ199904011.htmChen Xian-jin, Qi Huan, Wu Chong-jian, et al. Optimal design of two-stage mount isolation system with maxi mum entropy approach[J]. Journal of Vibration and Shock, 1999, 18(4): 45—49. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ199904011.htm [6] 解可新, 韩立兴, 林友联. 最优化方法[M]. 天津: 天津大学出版社, 1997. [7] 胡毓达. 实用多目标最优化[M]. 上海: 上海科学技术出版社, 1990. [8] 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997. [9] 陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 1989. [10] 陈新良, 陈龙珠, 叶贵如. 带Ruzicka隔振器的双层隔振系统参数优化[J]. 浙江大学学报, 1996, 23(2): 204—210. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC602.012.htmChen Xin-liang, Chen Long-zhu, Ye Gui-ru. Optimum parameters for double-layeredisolation system with Ruzicka isolator[J]. Journal of Zhejiang University, 1996, 23(2): 204—210. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC602.012.htm -
点击查看大图
图(3) / 表(4)
计量
- 文章访问数: 279
- HTML全文浏览量: 93
- PDF下载量: 240
- 被引次数: 0
