缺损钢筋混凝土梁桥模糊可靠性评价模型

吕颖钊; 贺拴海

缺损钢筋混凝土梁桥模糊可靠性评价模型

长安大学桥梁与隧道陕西省重点实验室, 陕西西安 710064

基金项目:

陕西省交通科技项目 03-08K

详细信息

作者简介:
吕颖钊(1978-)，男，浙江湖州人，长安大学博士研究生，从事在役桥梁可靠度研究

中图分类号: U441
计量
- 文章访问数: 290
- HTML全文浏览量: 147
- PDF下载量: 224
- 被引次数: 0
出版历程
- 收稿日期: 2005-07-25
- 刊出日期: 2005-12-25

Fuzzy reliability evaluation of defective RC beam bridge

Key Laboratory for Bridge and Tunnel of Shaanxi Province, Chang'an University, Xi'an 710064, China

More Information

Author Bio:
Lu Ying-zhao(1978-), male, doctoral student, 86-29-82334837, lyz117@126.com

摘要

摘要: 结合模糊评价理论、层次分析法以及概率可靠度方法, 建立了钢筋混凝土梁桥缺损状况模糊可靠性评价模型。通过建立模糊评价集, 确定项目层、指标层模糊评价因素集和模糊评价因素权重集, 构造概率型判断矩阵, 经加权平均值法计算, 得到梁桥缺损状况模糊评判得分, 以目标可靠指标和最低可靠指标为界, 将模糊评判得分转换为模糊可靠指标, 实现在役梁桥缺损状况的模糊可靠性评价。采用该方法对一座使用25年的多跨简支钢筋混凝土梁桥进行评价, 得到模糊可靠指标为3.769, 满足最低可靠指标要求, 与桥梁实际状况相符, 表明该方法可行。
- 桥梁工程 /
- 缺损状况 /
- 模糊评价 /
- 可靠度 /
- 模糊可靠指标
Abstract: In order to improve the safe evaluation reliability of bridge, a fuzzy reliability evaluation model of defective RC beam bridge was put forward by fuzzy evaluation theory, analytical hierarchy process method and probability method. Through establishing fuzzy evaluation criterion, determining item level factors, index level factors and their weight coefficients, constructing probabilistic matrix of membership degree, the score of fuzzy reliability evaluation of defective RC beam bridge was calculated by weighted average method. The score was switched to fuzzy reliability index by the bounds of target reliability index and lowest reliability index. An existing multi-span RC beam bridge with 25 years was evaluated by the method. Its fuzzy reliability index is 3.769, which accords with the bridge condition. The evaluation result indicates that the method is feasible.
- bridge engineering /
- defective condition /
- fuzzy evaluation /
- reliability /
- fuzzy reliability index

HTML全文

图 1 梁桥缺损状况评价模型

Figure 1. Evaluation model of defective beam bridge

下载: 全尺寸图片幻灯片

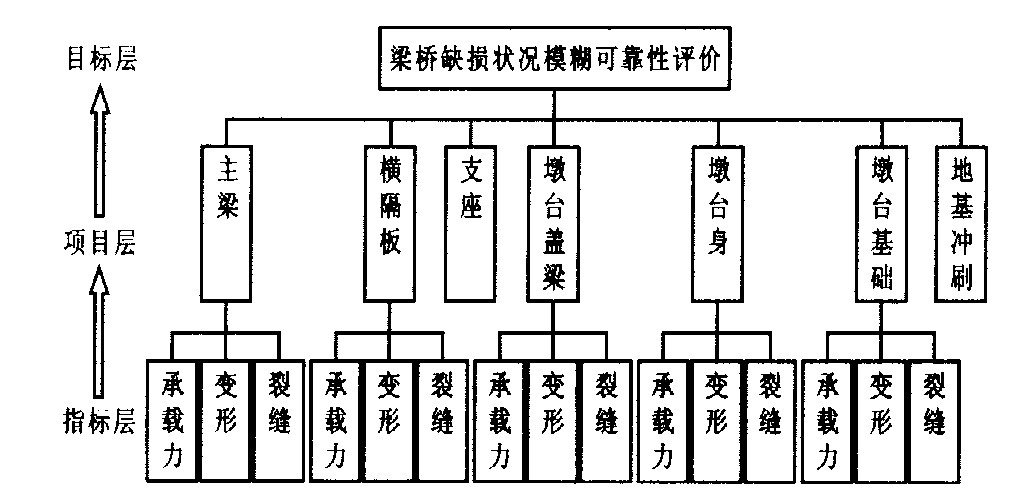
表 1 一级评判模型因素权重系数

Table 1. Weight coefficients of item level factors

部件i	部件名称	权重(α_i)
1	主梁	0.21
2	横隔板	0.06
3	支座	0.03
4	墩台盖梁	0.15
5	墩台身	0.23
6	墩台基础	0.24
7	地基冲刷	0.08

下载: 导出CSV

表 2 二级评判模型因素权重系数

Table 2. Weight coefficients of index level factors

下载: 导出CSV

表 3 公路桥梁结构的目标可靠指标

Table 3. Target reliability indices of highway bridges

下载: 导出CSV

参考文献(13)

[1]	JTGH11-2004, 公路桥涵养护规范[S].
[2]	李昌铸. 公路桥梁管理系统(CBMS2000)的开发与应用[J]. 公路交通科技, 2003, 20(3): 84—90. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200303021.htm Li Chang-zhu. Development and application of CBMS2000[J]. Journal of Highway and Transportation Research and Development, 2003, 20(3): 84—90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200303021.htm
[3]	魏朗, 高丽敏, 余强, 等. 驾驶员道路安全感受模糊评判模型[J]. 交通运输工程学报, 2004, 4(1): 102—105. http://transport.chd.edu.cn/article/id/200401025 Wei Lang, Gao Li-min, Yu Qiang, et al. Fuzzy evaluating model of driver's road safety perception[J]. Journal of Traffic and Transportation Engineering, 2004, 4(1): 102—105. (in Chi-nese). http://transport.chd.edu.cn/article/id/200401025
[4]	程晔, 曹文贵, 赵明华. 高速公路下伏岩溶顶板稳定性二级模糊综合评判[J]. 中国公路学报, 2003, 16(4): 21—24. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200304005.htm Cheng Ye, Cao Wen-gui, Zhao Ming-hua. Synthetic judgment on the two stage fuzzy of the stability of karst top slab beneath expressway[J]. China Journal of Highway and Transport, 2003, 16(4): 21—24. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200304005.htm
[5]	吕颖钊, 贺拴海. 在役桥梁承载力模糊可靠性的马尔科夫预测[J]. 长安大学学报(自然科学版), 2005, 25(4): 39—43. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200504010.htm Lu Ying-zhao, He Shuan-hai. Prediction of Markov fuzzy reliability for existing bridge[J]. Journal of Chang an University (Natural Science Edition), 2005, 25(4): 39—43. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200504010.htm
[6]	GB 50292-1999, 民用建筑可靠性鉴定标准[S].
[7]	肖萍. 桥梁技术状况评价与预测[D]. 西安: 长安大学, 2003.
[8]	浦聿修, 王庆霖, 姚继涛. 钢筋混凝土构件可靠性的综合评定[J]. 西安建筑科技大学学报, 1997, 29(4): 373—375. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ704.004.htm Pu Yu-xiu, Wang Qing-lin, YaoJi-tao. Onsynthetical evaluation of RC element reliability[J]. Xi an Jianzhu University of Architecture and Technology, 1997, 29(4): 373—375. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ704.004.htm
[9]	GB/T50283-1999, 公路工程结构可靠度设计统一标准[S].
[10]	赵挺生. 现存建筑物可靠性评价[J]. 建筑结构, 1998, 35(10): 41—45. https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG199810010.htm Zhao Ting-sheng. Reliability evaluation of existing buildings[J]. Building Structure, 1998, 35(10): 41—45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG199810010.htm
[11]	赵尚传, 赵国藩. 基于可靠性的在役混凝土结构剩余使用寿命预测[J]. 建筑科学, 2001, 17(5): 19—22. https://www.cnki.com.cn/Article/CJFDTOTAL-JZKX200105004.htm Zhao Shang-chuan, Zhao Guo-fan. Prediction of remaining service life of existing concrete structures based on reliability[J]. Building Science, 2001, 17(5): 19—22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZKX200105004.htm
[12]	周建方, 周美英, 李典庆. 现役钢闸门结构最低可靠度标准的确定[J]. 中国农村水利水电, 2003, 47(5): 48—51. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200305024.htm Zhou Jian-fang, Zhou Mei-ying, Li Dian-qing. Determining lowest dependability standardfor steel gate structure currently in use[J]. Water Conservancy and Hydroelectricity of Rural in China, 2003, 47(5): 48—51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200305024.htm
[13]	Vrouwenvelder T, Lovegrve R. Risk assessment and risk com-munication in civil engineering[A]. Safety, Risk, Reliability-Trends in Engineering[C]. Malta: I ABSE, 2001.