-
摘要: 为了保证飞行的安全性, 提高空域容量, 在提出了管制员工作负荷的统计方法和建立空域拓扑结构数学模型的基础上, 以各扇区工作负荷均衡为优化原则, 利用模拟退火随机优化算法对扇区最优化问题进行求解, 并使优化的新解满足空域划分的优先搜索、扇区连续性和扇区数最少原则。对厦门管制区的扇区最优划分实例分析表明, 3个扇区之间最大工作负荷之差为4.1 s, 小于规定的终止条件17.5 s, 验证了扇区优化方法是可行的。Abstract: In order to ensure flight security and increase airspace capability, in according to the balance rule of controller workload, a simulated annealing algorithm was adopted to solve sector optimum partition, which was based on the statistic method of controller workload and the mathematical model describing airspace topology structure. The new resolution satisfied the restriction of the three rules for airspace partition, they were preferential search, sector continuity and the minimum of sector number. The optimum result of Xiamen control airspace shows that the maximal workload difference among three sectors is 4.1 s, the value is smaller than 17.5 s, which indicates that the method is feasible.
-
表 1 部分常用管制用语工作负荷统计
Table 1. Part workload statistics of common control dictions
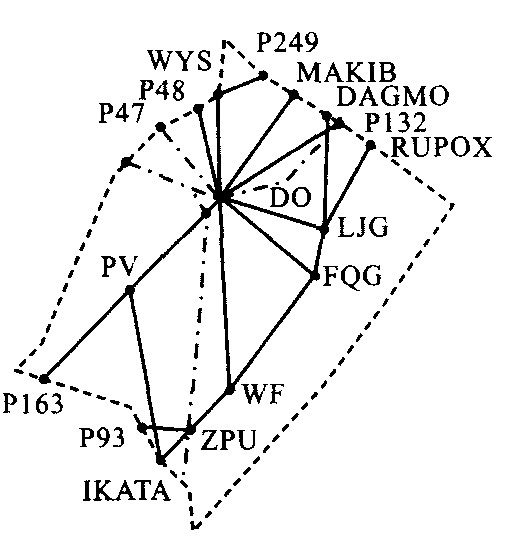
管制类型 管制种类 管制用语 工作负荷/s 一般用语 高度指令 在(高度)停止上升/下降 4.5 一般用语 活动通报 没有得到活动报告 3.5 一般用语 气象情报 报告飞行条件 3.5 机场管制 开车程序 开车时间自己掌握 4.0 机场管制 滑行程序 滑行时注意 3.5 机场管制 起飞许可 立即起飞, 否则在跑道外等待 4.7 进近管制 进近指令 保持目视间隔 4.2 进近管制 预计进近时间 没有延误 3.2 区域管制 管制许可 ATC许可(航空器呼号) 6.0 区域管制 紧急下降 紧急下降 3.1 
下载: 导出CSV
表 2 厦门终端区航段工作负荷
Table 2. Routes workloads of Xiamen control airspace
航段 负荷/s 航段 负荷/s IKATA-PV 27.1 P176-PV 21.3 IKATA-ZPU 27.4 P163-PV 7.2 ZPU-WF 18.9 P176-DO 0.0 WF-P169 34.1 LJG-DAGMO 10.2 FQG-LJG 9.1 IKATA-GUVIA 31.6 P84-DO 10.1 P93-ZPU 22.6 P48-DO 11.9 WF-P84 10.1 LJG-DO 9.3 P169-FQG 10.3 LJG-RUPOX 7.2 FQG-DO 14.0 DO-MAKIB 31.5 DO-P132 17.8 WYS-P249 22.1 DO-WYS 38.1 P47-DO 11.7
下载: 导出CSV
-
[1] Tofukuji N. An enroute ATC si mulation experi ment for sector capacity esti mation[A]. IEEE Transactions on Control Systems Technology[C]. New York: IEEE, 1993. [2] Delahaye D, Schoenauer M, Alliot J M. Airspace sectoring by evolutionary computation[A]. Proceeding of 10th IEEE Conference on Artificial Intelligence for Applications[C]. New York: IEEE, 1998. [3] Delahaye D, Alliot J M, Schoenauer M, et al. Genetic algorithms for partitioning airspace[A]. Proceeding of 10th IEEE Conference on Artificial Intelligence for Applications[C]. New York: IEEE, 1994. [4] 韩松臣, 张明, 黄卫芳. 管制扇区优化划分的方法及计算机实现技术[J]. 交通运输工程学报, 2003, 3(1): 101—104. http://transport.chd.edu.cn/article/id/200301023Han Song-chen, Zhang Ming, Huang Wei-fang. Method and computer technique for control sector optimum partition[J]. Journal of Traffic and Transportation Engineering, 2003, 3(1): 101—104. (in Chinese) http://transport.chd.edu.cn/article/id/200301023 -
点击查看大图
图(3) / 表(2)
计量
- 文章访问数: 225
- HTML全文浏览量: 83
- PDF下载量: 680
- 被引次数: 0
