Multilevel-fuzziness-comprehensiveness evaluation model of waterway net planning
Article Text (Baidu Translation)
-
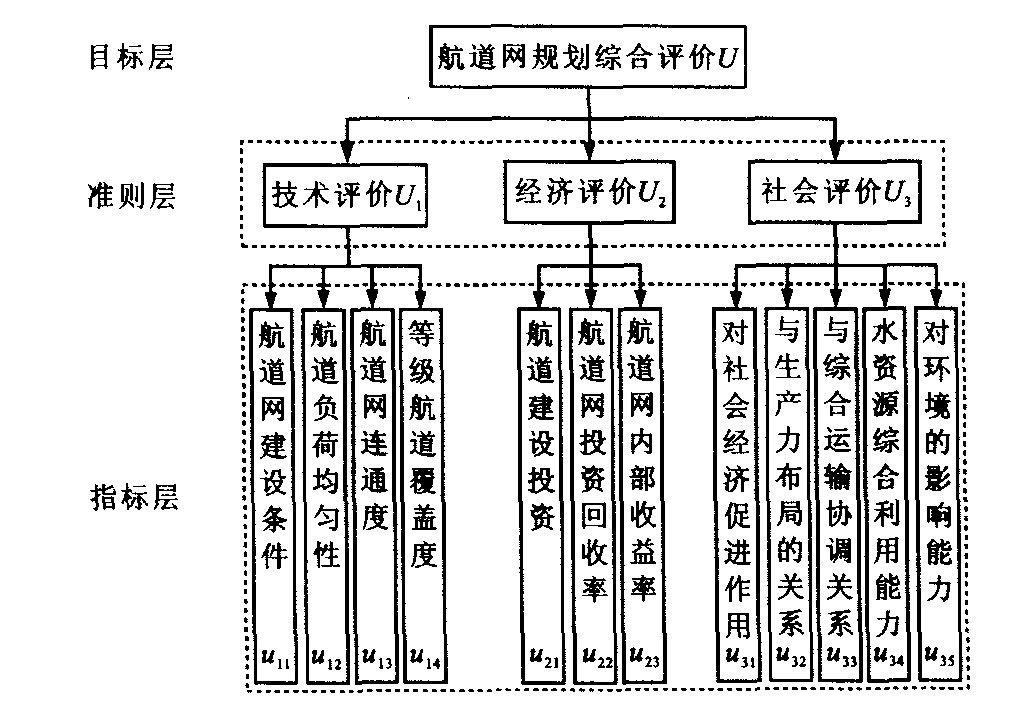
摘要: 为解决目前航道网规划评价中存在主观影响因素过多, 各评价指标权重不确定性等问题, 分析了航道网布局影响因素, 结合层次分析法, 提出了航道网规划方案的多目标、多级模糊综合评判方法。运用层次分析法确定各层次评价指标的权重, 运用模糊统计方法确定非定量指标的隶属度, 对于定量评价指标的隶属度, 则按效益型指标、适中型指标和成本型指标分别予以确定。对苏州市航道网规划方案评价结果表明, 该方法可客观地给出反映航道网实际情况的量化指标, 能够对航道网规划效果作出合理的定性评价。Abstract: There are many subjective factors and their weights can not been reasonably decided in current evaluation model for waterway net planning. Based on analyzing various factors affecting waterway net planning, a kind of multiobject and multi-layer fuzzy model for comprehensive assessment was proposed. Combined with AHP, the weights of the assessment indices were determined. With statistical method of fuzziness, the membership grades of non-quantitative indices were determined. The benefit index, the neutral index and the cost index were applied to define the memberships of quantitative indices. The evaluation result for Suzhou waterway net planning indicates that the model can provide quantitative indices of waterway net actual case objectively and evaluate the waterway net planning accurately.
-
表 1 各评价指标隶属度
Table 1. Membership grades of evaluation factors

-
[1] 姜晔, 褚志宇. 层次熵评价决策模型在航道网规划综合评价方面的应用[J]. 水运工程, 2001, 25(6): 30—34. doi: 10.3969/j.issn.1002-4972.2001.06.009Jiang Ye, Chu Zhi-yu. Application of AHP-entropy evaluation and decision model for comprehensive evaluation of waterway net planning[J]. Port and Waterway Engineering, 2001, 25(6): 30—34. (in Chinese) doi: 10.3969/j.issn.1002-4972.2001.06.009 [2] 黄显勇, 毛明海. 运用层次分析法对水利旅游资源进行定量评价[J]. 浙江大学学报(自然科学版), 2001, 28(3): 327—332. https://www.cnki.com.cn/Article/CJFDTOTAL-HZDX200103016.htmHuang Xian-yong, Mao Ming-hai. The quantitative evaluation of the tourismresources of water conservancy by using analytical hierarchy process[J]. Journal of Zhejiang University(Science Edition), 2001, 28(3): 327—332. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HZDX200103016.htm [3] 晏启鹏, 王忠强. AHP在公路主枢纽站场总体布局规划中的应用[J]. 西南交通大学学报, 1999, 34(2): 223—227. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT902.018.htmYan Qi-peng, Wang Zhong-qiang. Application of AHP to the general planning of yard and station of highway main hub[J]. Journal of Southwest Jiaotong University, 1999, 34(2): 223—227. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT902.018.htm [4] 王建军, 赵慧丽, 窦慧娟. 基于层次分析法的交通运输方案优选问题研究[J]. 石家庄铁道学院学报, 2004, 17(2): 45—48. doi: 10.3969/j.issn.2095-0373.2004.02.011Wang Jian-jun, Zhao Hui-li, Dou Hui-juan. Study on the basic of AHP in choosing traffic and transportation means[J]. Journal of Shijiazhuang Railway Institute, 2004, 17(2): 45—48. (in Chinese) doi: 10.3969/j.issn.2095-0373.2004.02.011 [5] 李铁柱, 刘勇, 卢璨, 等. 城市公共交通首末站综合评价[J]. 交通运输工程学报, 2005, 5(1): 86—91. http://transport.chd.edu.cn/article/id/200501021Li Tie-zhu, Liu Yong, Lu Can, et al. Comprehensive evaluation on original and terminal stations of urban public transport[J]. Journal of Traffic and Transportation Engineering, 2005, 5(1): 86—91. (in Chinese) http://transport.chd.edu.cn/article/id/200501021 [6] 梁军, 江薇, 李旭宏. 模糊综合评价方法改进及其在交通管理规划中的应用[J]. 交通运输工程学报, 2002, 2(4): 68—72. http://transport.chd.edu.cn/article/id/200204015Liang Jun, Jiang Wei, Li Xu-hong. An improvement on fuzzy comprehensive evaluation method and its use in urban traffic planning[J]. Journal of Traffic and Transportation Engineering, 2002, 2(4): 68—72. (in Chinese) http://transport.chd.edu.cn/article/id/200204015 [7] 黄健元. 模糊集及其应用[M]. 宁夏: 宁夏人民教育出版社, 1999. [8] 王众托. 系统工程引论[M]. 北京: 电子工业出版社, 1991. [9] 江苏省交通规划设计院, 苏州市交通局. 苏州市航道网规划报告[R]. 南京: 江苏省交通规划设计院, 2004. -





 下载:
下载: