基于转向的Logit交通分配算法

任刚; 王炜

基于转向的Logit交通分配算法

任刚,
王炜

东南大学江苏省交通规划与管理重点实验室, 江苏南京 210096

基金项目:

国家自然科学基金项目 50378016

详细信息

作者简介:
任刚(1976-)，男，浙江上虞人，东南大学讲师，博士，从事交通规划与管理研究

中图分类号: U491
计量
- 文章访问数: 261
- HTML全文浏览量: 110
- PDF下载量: 498
- 被引次数: 0
出版历程
- 收稿日期: 2005-07-21
- 刊出日期: 2005-12-25

Turn-based algorithm for Logit traffic assignment

REN Gang,
WANG Wei

Key Laboratory of Traffic Planning and Management for Jiangsu Province, Southeast University, Nanjing 210096, China

More Information

Author Bio:
Ren Gang(1976-), male, PhD, lecturer, 86-25-83795649, rengang@seu.edu.cn

摘要

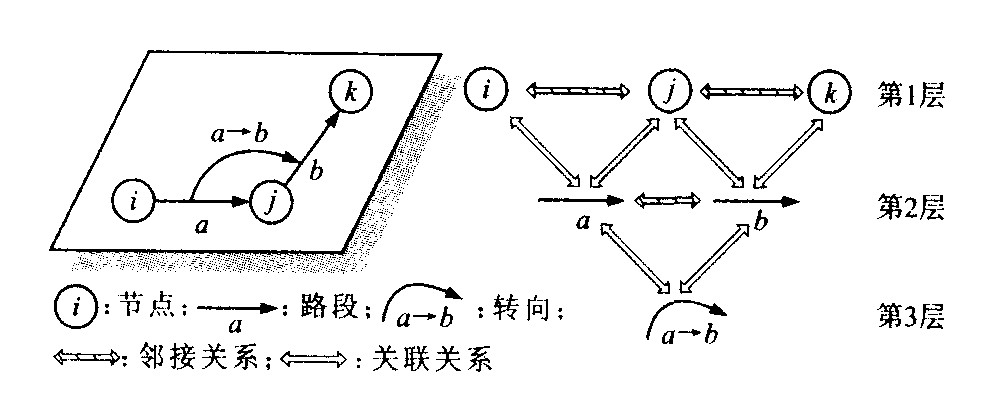
摘要: 为避免交通分配中传统的网络扩展法在处理转向延误时的缺陷, 通过分析网络基本要素节点、路段和转向之间的拓扑关系, 借鉴Dial算法的基本框架, 设计了一个基于转向的Logit交通分配算法。该算法以源点至路段的含转向延误的最短路径长度为依据处理各条路段, 正向计算转向权重, 反向分配路段流量和转向流量。算法计算结果与Logit路径流量和Dial算法数据相一致, 该算法可直接求解既满足Logit路径选择概率又考虑转向延误对交通分配影响的路段流量和转向流量模式, 而且Dial算法是其在转向延误为零时的一个特例。
- 道路交通规划 /
- Logit交通分配算法 /
- 转向延误 /
- Dial算法
Abstract: To overcome the shortcomings in traditional network-expanding method for handling turn delays in traffic assignment, a turn-based algorithm for Logit traffic assignment was developed with a similar framework of Dial algorithm, which was based on the topological relationships between network element nodes, links and turns. According to the origin-to-link-type shortest path distances with turn delays, all links were processed, turn weights were computed forward, and link flows and turn flows were assigned backward by the algorithm. Computation result shows that the flow assignment of the algorithm is identical to Logit-based path flows and Dial's algorithm data, the algorithm directly computes link flow and turn flow patterns, which not only agrees with Logit route-choice probability, but also counts for the effect of turn delays on traffic assignment, and Dial algorithm is a special case of the algorithm when all turn delays vanish.
- road traffic planning /
- Logit traffic assignment algorithm /
- turn delay /
- Dial algorithm

HTML全文

图 1 网络基本要素间的拓扑关系

Figure 1. Topological relationships of network elements

下载: 全尺寸图片幻灯片

图 2 算例网络

Figure 2. Example network

下载: 全尺寸图片幻灯片

图 3 路段流量和转向流量

Figure 3. Link flows and turn flows

下载: 全尺寸图片幻灯片

表 1 算法的区别与联系

Table 1. Difference and similarity of algorithms

比较项	Dial算法	本文算法
路径概念	节点到节点; 路径阻抗不带转向延误	节点到路段; 路径阻抗带转向延误
有效路径	由有效路段组成; 有效路段的终止节点比起始节点更远离出行起点	由有效转向组成; 有效转向的终止路段比起始路段更远离出行起点
路径算法	一般的最短路径算法	带转向延误的最短路径算法
算法依据	节点-路段拓扑关系; 节点处的流量守恒	路段-转向拓扑关系(包括节点-路段拓扑关系); 路段上的流量守恒
中间参数	路段似然值及权重	转向似然值及权重
输出结果	路段流量	转向流量和路段流量
算法效率	时间和空间开销主要取决于路段数目	时间和空间开销主要取决于转向数目
两者联系	算法基本框架一致; Dial算法是本文算法在转向延误为零时的一个特例

下载: 导出CSV

表 2 路段阻抗和转向延误

Table 2. Link impedances and turn delays

路段a		1		2		3		4		5		6		7		8		9		10		11		12
t $_{a}^{①}$		2		2		2		2		2		1		1		2		2		2		2		2
转向a→b	1→2		1→4		2→5		3→6		3→8	4→7	4→9		5→10		6→7		6→9		7→10		8→11		9→12		11→12
d_ab	0.0		0.5		0.0		1.0		0.5	0.5	1.5		0.0		1.5		0.5		0.5		1.0		1.0		0.5
注: ①该行数据与文献[[1]]中Dial算法的算例一致。

下载: 导出CSV

表 3 Step 1的计算结果

Table 3. Computation result of Step 1

路段a	γ		1		2		3			4		5		6		7		8		9		10			11		12		ζ
r (a)	0.0		2.0		4.0		2.0			4.5		6.0		4.0		6.0		4.5		6.5		8.0			7.5		9.5		∞
转向a→b	γ→1	γ→3		1→2		1→4		2→5	3→6		3→8		4→7		4→9	5→10	6→7		6→9		7→10		8→11	9→12		11→12		10→ζ		12→ζ
L_ab	0.135 3	0.135 3		0.135 3		0.082 1		0.135 3	0.135 3		0.082 1		0.223 1		0.030 2	0.135 3	0.082 1		0.082 1		0.082 1		0.049 8	0.049 8		0.082 1		1.000 0		1.000 0

下载: 导出CSV

表 4 Step 2、Step 3的计算过程及结果

Table 4. Computation procedures and results of Step 2 and Step 3

Step 2:计算w_ab, ∀b∈F (a)	路段a	Step 3:计算x_a及y_ca, ∀c∈B (a)
w_γ→1=L_γ→1=0.135 3↓	γ	x_γ=y_γ→1+y_γ→3=1 000	结束
w_γ→3=L_γ→3=0.135 3
w_1→2=L_1→2w_γ→1=0.018 3	1	x₁=y_1→2+y_1→4=695	y_γ→1=x₁=695
w_1→4=L_1→4w_γ→1=0.011 1
w_3→6=L_3→6w_γ→3=0.018 3	3	x₃=y_3→6+y_3→8=305	y_γ→3=x₃=305
w_3→8=L_3→8w_γ→3=0.011 1
w_2→5=L_2→5w_1→2=0.002 5	2	x₂=y_2→5=420	y_1→2=x₂=420
w_6→7=L_6→7w_3→6=0.001 5	6	x₆=y_6→7+y_6→9=248	y_3→6=x₆=248
w_6→9=L_6→9w_3→6=0.001 5
w_4→7=L_4→7w_1→4=0.002 5	4	x₄=y_4→7+y_4→9=275	y_1→4=x₄=275
w_4→9=L_4→9w_1→4=0.000 3
w_8→11=L_8→11w_3→8=0.000 6	8	x₈=y_8→11=57	y_3→8=x₈=57
w_5→10=L_5→10w_2→5=0.000 3	5	x₅=y_5→10=420	y_2→5=x₅=420
w_7→10=L_7→10 (w_4→7+w_6→7) =0.000 3	7	x₇=y_7→10=409	y_4→7=x₇w_4→7/ (w_4→7+w_6→7) =255
			y_6→7=x₇w_6→7/ (w_4→7+w_6→7) =154
w_9→12=L_9→12 (w_4→9+w_6→9) =0.000 1	9	x₉=y_9→12=114	y_4→9=x₉w_4→9/ (w_4→9+w_6→9) =20
			y_6→9=x₉w_6→9/ (w_4→9+w_6→9) =94
w_11→12=L_11→12w_8→11=0.000 0	11	x₁₁=y_11→12=57	y_8→11=x₁₁=57
w_10→ζ=L_10→ζ (w_5→10+w_7→10) =0.000 7	10	x₁₀=y_10→ζ=829	y_5→10=x₁₀w_5→10/ (w_5→10+w_7→10) =420
			y_7→10=x₁₀w_7→10/ (w_5→10+w_7→10) =409
w_12→ζ=L_12→ζ (w_9→12+w_11→12) =0.000 1	12	x₁₂=y_12→ζ=171	y_9→12=x₁₂w_9→12/ (w_9→12+w_11→12) =114
			y_11→12=x₁₂w_11→12/ (w_9→12+w_11→12) =57
结束	ζ	↑x_ζ=q=1 000	y_10→ζ=x_ζw_10→ζ/ (w_10→ζ+w_12→ζ) =829
			y_12→ζ=x_ζw_12→ζ/ (w_10→ζ+w_12→ζ) =171

下载: 导出CSV

表 5 路径流量

Table 5. Path flows

路径(节点序列)	路径阻抗	选择概率	路径流量
1-2-3-6-9	8.0	0.419 7	420
1-2-5-6-9	8.5	0.254 6	255
1-2-5-8-9	11.0	0.020 9	20
1-4-7-8-9	10.0	0.056 8	57
1-4-5-8-9	9.5	0.093 6	94
1-4-5-6-9	9.0	0.154 4	154

下载: 导出CSV

参考文献(10)

[1]	Dial R B. A probabilistic multipath traffic assignment algorithm which obviates path enumeration[J]. Transportation Research, 1971, 5 (2): 83—111. doi: 10.1016/0041-1647(71)90012-8
[2]	刘海旭, 蒲云. 基于行程质量的随机用户平衡分配模型[J]. 中国公路学报, 2004, 17 (4): 93—95. doi: 10.3321/j.issn:1001-7372.2004.04.020 Liu Hai-xu, Pu Yun. Stochastic user equilibrium assignment model based on travel trait[J]. China Journal of Highway and Transport, 2004, 17 (4): 93—95. (in Chinese) doi: 10.3321/j.issn:1001-7372.2004.04.020
[3]	Bell M G H. Alternative to Dial s Logit assignment algorithm[J]. Transportation Research, 1995, 29B (4): 287—295.
[4]	Akamatsu T. Cyclic flows. Marcov process and stochastic traffic assignment[J]. Transportation Research, 1996, 30B (5): 369—386.
[5]	Damberg O, Lundgren J T, Patriksson M. An algorithm for the stochastic user equilibrium problem[J]. Transportation Research, 1996, 30B (2): 115—131.
[6]	Meneguzzer C. An equilibriumroute choice model with explicit treat ment of the effect of intersections[J]. Transportation Research, 1995, 29B (5): 329—356.
[7]	王丰元, 潘福全, 张丽霞, 等. 基于交通限制的路网最优路径算法[J]. 交通运输工程学报, 2005, 5 (1): 92—95. http://transport.chd.edu.cn/article/id/200501022 Wang Feng-yuan, Pan Fu-quan, Zhang Li-xia, et al. Optimal path algorithm of road network with traffic restriction[J]. Journal of Traffic and Transportation Engineering, 2005, 5 (1): 92—95. (in Chinese) http://transport.chd.edu.cn/article/id/200501022
[8]	任刚, 王炜, 邓卫. 带转向延误和限制的最短路径问题及其求解方法[J]. 东南大学学报, 2004, 34 (1): 104—108. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX200401024.htm Ren Gang, Wang Wei, Deng Wei. Shortest path problem with turn penalties and prohibitions andits solutions[J]. Journal of Southeast University, 2004, 34 (1): 104—108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX200401024.htm
[9]	Kirby R F, Potts R B. The mini mumroute problemfor networks with turn penalties and prohibitions[J]. Transportation Research, 1969, 3 (4): 397—408.
[10]	Ziliaskopoulos A K, Mahmassani H S. A note on least time path computation considering delays and prohibitions for intersection movements[J]. Transportation Research, 1996, 30B (5): 359—367.