居民出行分布的熵模型及其参数标定

姚荣涵; 王殿海

居民出行分布的熵模型及其参数标定

吉林大学交通学院, 吉林长春 130025

基金项目:

国家自然科学基金项目 70071039

吉林省杰出青年基金项目 20010114

高等学校骨干教师计划项目 1000

详细信息

作者简介:
姚荣涵(1979-)，女，山西运城人，吉林大学博士研究生，从事交通运输规划研究

中图分类号: U491.1
计量
- 文章访问数: 327
- HTML全文浏览量: 87
- PDF下载量: 257
- 被引次数: 0
出版历程
- 收稿日期: 2005-07-13
- 刊出日期: 2005-12-25

Entropy models of inhabitant trip distributions and parameters calibration

School of Transportation, Jilin University, Changchun 130025, China

More Information

Author Bio:
Yao Rong-han(1979-), female, doctoral student, 86-431-5095857, cyanyrh@yahoo.com.cn

摘要

摘要: 为寻求一种描述各种出行分布情况的普适性模型, 运用最大信息熵原理, 结合数理统计方法, 建立了以原点矩均值为约束条件的新模型体系。为确定模型参数, 提出了熵模型的参数标定方法, 利用长春市居民出行调查数据对参数标定方法进行了验证。数据验证结果显示, 对于步行、自行车、公交车和小汽车四种出行方式, 最高阶原点矩的阶数分别取3、4、5时, 所有模型均通过置信度为95%的χ²检验。通过χ²值和分布曲线的比较发现, 不同出行方式取得最好效果的最高阶原点矩的阶数并不一致, 这种差异取决于出行方式的内在特性。居民出行分布的信息熵模型可以定量描述任意出行方式的分布规律, 所提出的参数标定方法简单有效。
- 交通规划 /
- 出行分布 /
- 最大信息熵原理 /
- 熵模型
Abstract: In order to find some general models to describe all kinds of inhabitant trip distributions, according to the maximum information entropy theory and statistics, new models under the constraints of the means of origin moments were built, a parameters calibration method was put forward to ascertain the parameters of the models. They were validated by the inhabitant trip survey data in Changchun city. The trip modes of walk, bike, bus and car pass χ² tests with 95% confidence when their orders of the highest origin moments are 3, 4 and 5 respectively. The comparison of χ² values and inhabitant trip distributions curves shows that the orders are different when the best effects of all trip modes are gotten. The differences result from the inner characteristics of trip modes. Analyzing result indicates that the information entropy models can quantificationally describe the distribution principle of any trip mode, the parameters validation method is simple and effective.
- traffic planning /
- trip distribution /
- maximum information entropy theory /
- entropy model

HTML全文

图 1 步行出行分布曲线

Figure 1. Trip distribution curves by walk

下载: 全尺寸图片幻灯片

图 2 自行车出行分布曲线

Figure 2. Trip distribution curves by bike

下载: 全尺寸图片幻灯片

图 3 公交车出行分布曲线

Figure 3. Trip distribution curves by bus

下载: 全尺寸图片幻灯片

图 4 小汽车出行分布曲线

Figure 4. Trip distribution curves by car

下载: 全尺寸图片幻灯片

表 1 居民出行分布的熵模型

Table 1. Entropy models of inhabitant trip distributions

m取值	模型
3	p_i=exp(-λ-λ₁d_i-λ₂d_i²-λ₃d_i³)
4	p_i=exp(-λ-λ₁d_i-λ₂d_i²-λ₃d_i³-λ₄d_i⁴)
5	p_i=exp(-λ-λ₁d_i-λ₂d_i²-λ₃d_i³-λ₄d_i⁴-λ₅d_i⁵)

下载: 导出CSV

表 2 步行出行分布

Table 2. Trip distribution by walk

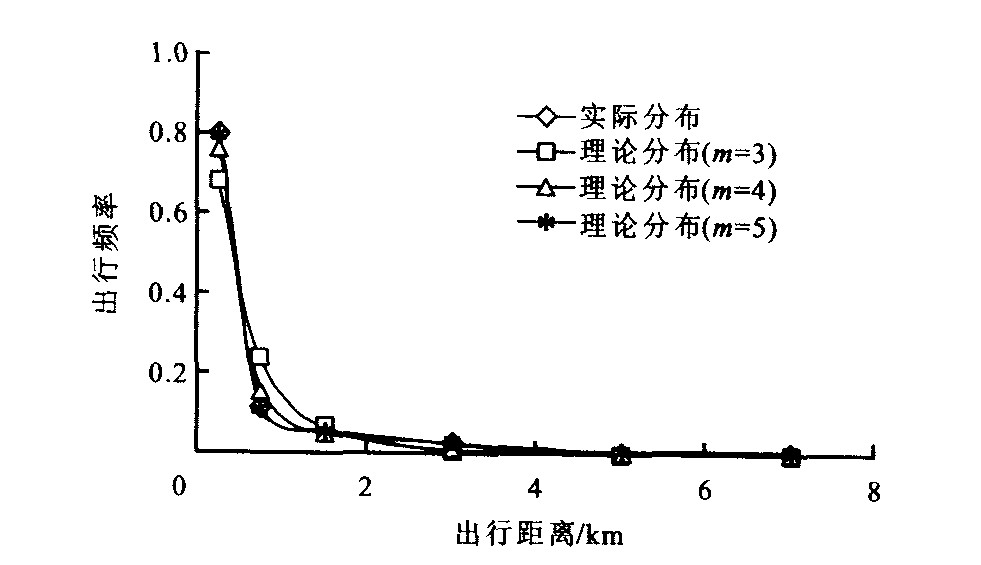
出行距离/km	实际分布	理论分布(m=3)	理论分布(m=4)	理论分布(m=5)
< 0.5	0.799 3	0.685 8	0.763 6	0.796 3
0.5~1.0	0.112 9	0.237 7	0.157 6	0.112 5
1.0~2.0	0.059 2	0.061 3	0.049 4	0.059 0
2.0~4.0	0.022 5	0.008 9	0.023 9	0.022 8
4.0~6.0	0.004 0	0.002 8	0.003 5	0.004 7
> 6.0	0.002 0	0.003 4	0.002 0	0.004 8
合计	1.0	1.0	1.0	1.0
χ²值	—	316.078 2	49.040 3	5.125 6
χ²临界值	3 126.2
检验结果	—	通过	通过	通过

下载: 导出CSV

表 3 自行车出行分布

Table 3. Trip distribution by bike

出行距离/km	实际分布	理论分布(m=3)	理论分布(m=4)	理论分布(m=5)
< 0.5	0.041 4	0.052 9	0.043 7	0.041 9
0.5~1.0	0.190 8	0.146 9	0.148 0	0.193 0
1.0~2.0	0.321 5	0.356 0	0.375 3	0.325 2
2.0~4.0	0.357 1	0.362 0	0.336 4	0.358 9
4.0~6.0	0.071 2	0.061 6	0.077 7	0.067 5
> 6.0	0.018 1	0.020 7	0.018 9	0.013 5
合计	1.0	1.0	1.0	1.0
χ²值	—	39.222 3	41.514 2	3.453 2
χ²临界值	2 002.2
检验结果	—	通过	通过	通过

下载: 导出CSV

表 4 公交车出行分布

Table 4. Trip distribution by bus

出行距离/km	实际分布	理论分布(m=3)	理论分布(m=4)	理论分布(m=5)
< 0.5	0.010 3	0.019 6	0.010 0	0.008 5
0.5~1.0	0.040 2	0.043 8	0.042 8	0.033 1
1.0~2.0	0.153 8	0.112 9	0.144 3	0.126 6
2.0~4.0	0.280 6	0.327 2	0.284 3	0.233 5
4.0~6.0	0.377 1	0.353 3	0.375 1	0.357 6
> 6.0	0.138 1	0.143 2	0.143 6	0.240 8
合计	1.0	1.0	1.0	1.0
χ²值	—	57.104 4	2.152 6	126.812
χ²临界值	2 167.3
检验结果	—	通过	通过	通过

下载: 导出CSV

表 5 小汽车出行分布

Table 5. Trip distribution by car

出行距离/km	实际分布	理论分布(m=3)	理论分布(m=4)	理论分布(m=5)
< 0.5	0.029 6	0.025 7	0.026 3	0.023 1
0.5~1.0	0.022 2	0.039 7	0.038 8	0.017 3
1.0~2.0	0.096 3	0.070 2	0.069 6	0.075 1
2.0~4.0	0.148 1	0.168 4	0.182 5	0.116 1
4.0~6.0	0.333 3	0.324 3	0.329 0	0.283 9
> 6.0	0.370 4	0.371 7	0.353 8	0.484 5
合计	1.0	1.0	1.0	1.0
χ²值	—	2.789 4	3.391 7	7.222 8
χ²临界值	167.206 1
检验结果	—	通过	通过	通过

下载: 导出CSV

表 6 结果比较

Table 6. Results comparison

出行方式	理论分布(m=3)	理论分布(m=4)	理论分布(m=5)
步行	不好	次好	最好
自行车	次好	不好	最好
公交车	次好	最好	不好
小汽车	最好	次好	不好

下载: 导出CSV

参考文献(12)

[1]	沃尔特. 赫利, 胡运权. 城市系统模型[M]. 哈尔滨: 哈尔滨工业大学出版社, 1987.
[2]	杨兆升. 交通运输系统规划[M]. 北京: 人民交通出版社, 1998.
[3]	杨兆升. 运输系统规划与模型[M]. 北京: 人民交通出版社, 1996.
[4]	王炜, 徐吉谦, 杨涛, 等. 城市交通规划[M]. 南京: 东南大学出版社, 1999.
[5]	王殿海, 杨兆升, 雷雨龙. 模拟电子云居民分布模型研究[J]. 系统工程理论与实践, 1996, 16(7): 71—74. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL607.012.htm Wang Dian-hai, Yang Zhao-sheng, Lei Yu-long. Research on the inhabitants distribution model by simulation electron cloud[J]. Systems Engineering———Theory and Practice, 1996, 16(7): 71—74. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL607.012.htm
[6]	周雪梅, 曲大义, 贾洪飞. 信息化条件下的城市交通需求预测[J]. 长安大学学报(自然科学版), 2003, 23(3): 88—90. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200303025.htm Zhou Xue-mei, Qu Da-yi, Jia Hong-fei. Urban transportation demands prediction in information society[J]. Journal of Chang an University(Natural Science Edition), 2003, 23(3): 88—90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200303025.htm
[7]	李景, 彭国雄. 由路段交通量推算OD出行量方法研究[J]. 交通运输工程学报, 2001, 1(2): 78—82. http://transport.chd.edu.cn/article/id/200102019 Li Jing, Peng Guo-xiong. A study on estimating OD trips from observedlink flows[J]. Journal of Traffic and Transportation Engineering, 2001, 1(2): 78—82. (in Chinese) http://transport.chd.edu.cn/article/id/200102019
[8]	裴玉龙, 刘洋, 罗丽君. 公路网路段交通量预测模型研究[J]. 中国公路学报, 1999, 12(4): 101—106. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL199904017.htm Pei Yu-long, Liu Yang, Luo Li-jun. Model study of highway traffic section volume prediction[J]. China Journal of Highway and Transport, 1999, 12(4): 101—106. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL199904017.htm
[9]	哈肯. 信息与自组织[M]. 成都: 四川教育出版社, 1988.
[10]	哈肯. 协同学[M]. 北京: 原子能出版社, 1984.
[11]	俞礼军, 严海, 严宝杰. 最大熵原理在交通流统计分布模型中的应用[J]. 交通运输工程学报, 2001, 1(3): 91—94. http://transport.chd.edu.cn/article/id/200103023 Yu Li-jun, Yan Hai, Yan Bao-jie. Maximum entropy method and it's application in probability density function of traffic flow[J]. Journal of Traffic and Transportation Engineering, 2001, 1(3): 91—94. (in Chinese) http://transport.chd.edu.cn/article/id/200103023
[12]	刘伟平. 交通OD表的实用计算模型[J]. 中国公路学报, 1995, 8(3): 18—24. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL503.004.htm Liu Wei-ping. Apractical computation model of traffic OD table[J]. China Journal of Highway and Transport, 1995, 8(3): 18—24. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL503.004.htm