Nonlinear stability analysis of long-span curve bridge with high piers during cantilever construction
-
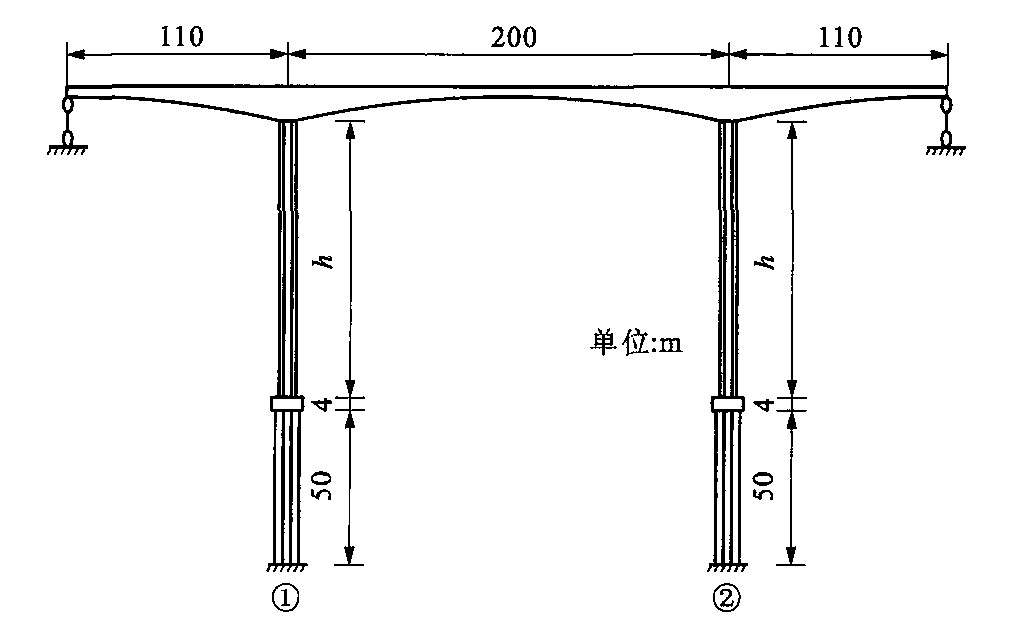
摘要: 以非线性稳定理论为基础, 以高墩大跨径弯桥悬臂施工阶段的结构稳定性为研究对象, 利用有限元法对其在悬臂施工阶段荷载状态各工况分别进行考虑材料非线性和结构大变形与材料非线性的双非线性稳定性分析, 计算了不同工况、不同曲线圆心角、不同墩身长细比、不同系梁个数的刚构桥在悬臂施工阶段非线性稳定系数和悬臂端位移, 对计算结果进行了分析, 归纳出高墩大跨径弯桥悬臂施工阶段非线性稳定荷载系数和悬臂端位移与桥梁曲线圆心角、墩身长细比及系梁个数的关系。结果显示: 非线性稳定荷载约为特征值屈曲荷载的35%, 弯桥曲线圆心角对非线性稳定荷载系数和悬臂端位移的影响更为突出, 多个系梁对悬臂施工的稳定并非有利。Abstract: In order to improve the structure stability of curve rigid frame bridge with high pier and long-span during cantilever construction, bridge structure geometry nonlinearity and material nonlinearity were considered, the stabilities and max-displacements of the bridge were analyzed by finite element method with different central angles of curve, different slenderness ratios of pier and different tie-girder numbers in each situation, the relations of bridge critical stability coefficient and max-displacement with the central angle of curve, slenderness ratio of pier and tie-girder number were studied. The result shows that the nonlinear stability coefficient of bridge is 35% of eigenvalue flexure load, the central angle of curve dominates the critical stability coefficient and the max-displacement, it is not favorable for bridge stability that the number of tie-girder is more than two.
-
图 3 失稳荷载与墩身长细比关系曲线
Figure 3. Relationship of stability coefficient and length-slender-ratio
表 1 稳定系数计算结果
Table 1. Computation result of stability coefficient
工况 线弹性 几何非线性 材料非线性 双重非线性 1 7.622 5 7.371 8 3.631 8 2.677 3 2 7.681 6 7.371 8 3.631 8 2.677 3 3 7.863 6 7.192 4 3.663 2 2.791 1 4 7.746 4 7.371 8 3.631 8 2.677 3 5 7.746 4 7.371 8 3.631 8 2.677 3 
下载: 导出CSV
表 2 非线性稳定系数计算结果
Table 2. Computation result of nonlinear stability parameter
曲率参数 墩身长细比 半径/m 圆心角/ (°) 33.153 37.297 41.441 45.585 49.729 53.873 58.017 62.167 66.306 ∞ 0.00 7.220 1 6.738 6 6.376 9 5.876 9 5.376 9 4.892 3 4.437 5 4.003 6 3.585 9 500 22.92 4.270 6 3.991 0 3.722 5 3.450 0 3.225 0 2.980 8 2.770 6 2.566 1 2.371 8 400 28.65 3.937 5 3.677 3 3.437 5 3.202 5 2.990 8 2.780 6 2.586 6 2.402 3 2.225 0 300 38.20 3.470 5 3.266 0 3.055 6 2.867 3 2.667 3 2.500 0 2.336 3 2.177 3 2.030 5 250 45.82 3.142 3 2.960 0 2.780 6 2.611 3 2.447 5 2.280 6 2.131 8 2.000 0 1.856 8 200 57.30 2.826 3 2.677 3 2.520 5 2.381 8 2.245 5 2.101 3 1.980 5 1.856 8 1.735 0 150 76.39 2.356 8 2.235 0 2.121 8 2.000 0 1.892 3 1.780 6 1.677 3 1.576 1 1.480 5 100 114.59 1.555 6 1.480 0 1.402 3 1.326 3 1.255 5 1.177 3 1.111 3 1.055 6 0.980 8
下载: 导出CSV
表 3 位移计算结果
Table 3. Computation result of displacement
曲率参数 墩身长细比 半径/m 圆心角/ (°) 33.153 37.297 41.441 45.585 49.729 53.873 58.017 62.167 66.306 500 22.92 2.879 2.820 2.823 2.789 2.727 2.938 3.223 3.308 3.484 400 28.65 2.792 2.744 2.758 2.861 2.950 3.068 3.193 3.433 3.574 300 38.20 2.670 2.714 2.767 2.922 3.002 3.118 3.426 3.693 3.933 250 45.82 2.684 2.772 2.892 3.065 3.297 3.412 3.646 4.114 4.173 200 57.30 2.600 2.727 2.858 3.095 3.349 3.484 3.869 4.156 4.322 150 76.39 2.919 3.079 3.343 3.448 3.835 4.087 4.403 4.602 5.213 100 114.59 3.799 4.117 4.288 4.584 5.097 5.230 5.806 5.685 6.413
下载: 导出CSV
表 4 稳定系数
Table 4. Stability coefficients
系梁个数 0 1 2 3 5 特征值屈曲荷载系数 7.623 8.095 8.064 8.032 7.968 非线性稳定荷载系数 2.667 2.677 2.667 2.647 2.632
下载: 导出CSV
-
[1] 王振阳, 赵煜, 徐兴. 高墩大跨径桥梁稳定性[J]. 长安大学学报: 自然科学版, 2003, 23(4): 38-40. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200304010.htmWang Zhen-yang, Zhao Yu, Xu Xing. Three dimension stability of bridge with high piers[J]. Journal of Chang'an University: Natural Science Edition, 2003, 23(4): 38-40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200304010.htm [2] 乐云祥, 任飞, 常英. 高桩承台的稳定性分析[J]. 桥梁建设, 2004, 34(1): 16-19. https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD202106023.htmYue Yun-xiang, Ren Fei, Chang Ying. Stability analysis of elevated pile caps[J]. Bridge Construction, 2004, 34(1): 16-19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD202106023.htm [3] 王钧利, 贺拴海. 钢筋混凝土高墩稳定非线性分析和模型试验[J]. 长安大学学报: 自然科学版, 2005, 25(4): 31-34.Wang Jun-li, He Shuan-hai. Nonlinear stability and model test of reinforce concrete for high piers[J]. Journal of Chang'an University: Natural Science Edition, 2005, 25(4): 31-34. (in Chinese) [4] Mirza S A, Lacroix E A. Comparative study of strength-computation methods for rectangular reinforced concrete columns[J]. ACI Structural Journal, 2002, 99(4): 399-410. [5] Moyer M J, Kowalsky M J. Influence of tension strain on buckling of reinforcement in concrete columns[J]. ACI Structural Journal, 2003, 100(1): 75-85. [6] 丁汉山, 刘华. 高架桥弯梁抗扭稳定性分析[J]. 交通运输工程学报, 2004, 4(3): 44-48. http://transport.chd.edu.cn/article/id/200403011Ding Han-shan, Liu Hua. Analysis of torsional stability for curve beam in elevated bridges[J]. Journal of Traffic and Transportation Engineering, 2004, 4(3): 44-48. (in Chinese) http://transport.chd.edu.cn/article/id/200403011 [7] 郑一峰, 黄桥, 冷曦晨. 预弯组合梁桥的弹塑性极限承载能力研究[J]. 中国公路学报, 2005, 18(4): 54-58. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200504010.htmZheng Yi-feng, Huang Qiao, Leng Xi-chen. Research on elasticplastic ultimate capacity of preflex beam bridges[J]. China Journal of Highway and Transport, 2005, 18(4): 54-58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200504010.htm [8] 赵伟封, 马宝林, 陈谐民, 等. 薄壁特高墩预应力混凝土连续刚构桥的空间稳定性[J]. 长安大学学报: 自然科学版, 2004, 24(4): 51-54. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200404012.htmZhao Wei-feng, Ma Bao-lin, Chen Xie-min, et al. Space stability of prestressed concrete continuous rigid frame bridge with tall pier and thin wall[J]. Journal of Chang'an University: Natural Science Edition, 2004, 24(4): 51-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200404012.htm -
点击查看大图
图(6) / 表(4)
计量
- 文章访问数: 324
- HTML全文浏览量: 101
- PDF下载量: 416
- 被引次数: 0
