Model and heuristic solution for location routing problems of logistics network
Article Text (Baidu Translation)
-
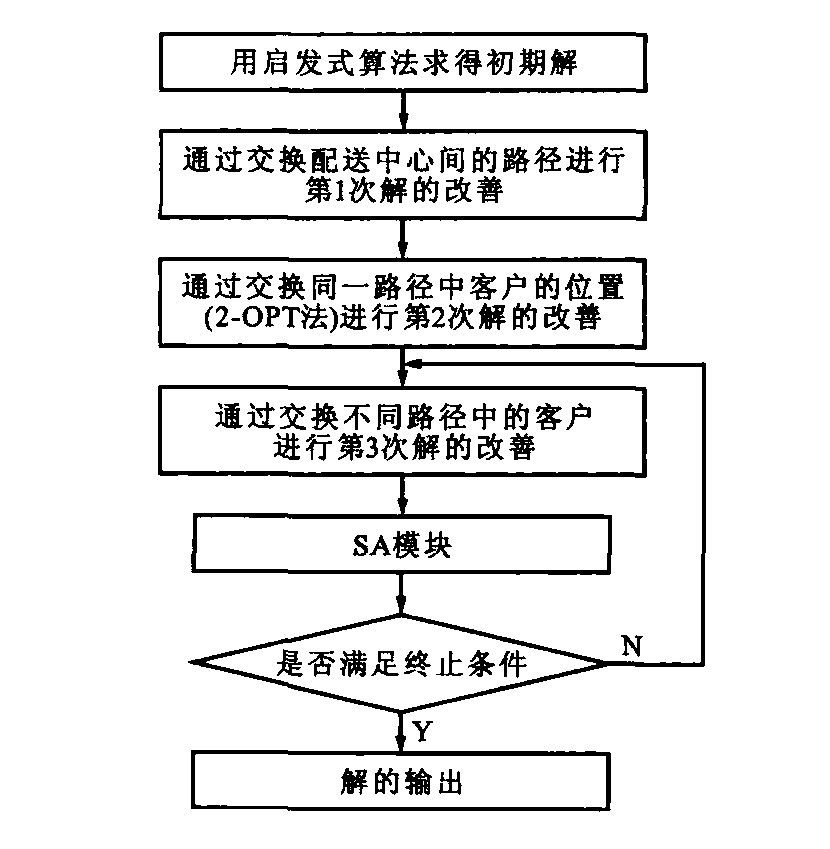
摘要: 以商品从供应商, 经过物流中心(或配送中心), 配送到最终用户的整个过程中所产生的费用最小化为目标函数, 提出了求解供应商的最佳位置与数量、配送中心的最佳位置与数量以及从配送中心到最终用户的最佳配送路径优化问题, 建立了问题的数学模型, 利用传统启发式算法与模拟退火法开发了问题求解的混合启发式解法, 并利用人工生成数据和实例进行了计算验证。对于小规模问题, 通过与数理规划软件所求得的最优解进行比较可以看出, 所提出的数学模型可以准确地描述此类问题, 所提出的混合启发式解法能够在短时间内求解问题, 并得到非常接近于最优解的近似解; 对于大规模问题, 虽然无法求得最优解进行比较, 但从实例计算结果来看, 所求解也是较好的, 因此可以认为所提出的解法是有效和良好的, 具有较高的实用价值。Abstract: The minimum cost related to the process, in which goods are delivered from suppliers, through logistics centers (or distribution centers) to ultimate customers, was taken as the object function, MSDLRP (multi-supplier multi-depot location routing problem) was presented, including the optimal number and locations of suppliers, the optimal number and locations of distribution centers, the optimal routes from distribution centers to ultimate customers, a mathematic model of the problem was put forward, a mixed heuristic solution was developed by using traditional heuristic solution and simulated annealing solution, they were tested by manually generated data and studied cases.For small-scaled problem, compared with the optimal result got by using planning software, MSDLRP can be described by the mathematic model accurately, the problem can be solved by the heuristic solution during short period, and the optimal result is obtained.For big-scaled problem, although the optimal result can not be got, the result also is better.
-
表 1 小规模问题的计算结果
Table 1. Computation result of small-scaled problem
最优解 问题规模 目标值 运行时间/s NG=3, NT=3, NC=8 388.5 3 NG=3, NT=3, NC=10 421.2 21 NG=3, NT=3, NC=12 685.0 580 NG=3, NT=3, NC=14 874.1 162 000 注: NG为供应商数量, NT为配送中心数量, NC为客户数量。 
下载: 导出CSV
表 2 最优解与近似解比较
Table 2. Comparison of optimal solution and approximate solution
问题规模 最优解 近似解 误差/% 目标值 运行时间/s 目标值 运行时间/s NG=3, NT=3, NC=8 388.5 3 396.5 < 1 2.1 NG=3, NT=3, NC=10 421.2 21 421.2 < 1 0.0 NG=3, NT=3, NC=12 685.0 580 692.0 < 1 1.0 NG=3, NT=3, NC=14 874.1 162 000 889.5 < 1 2.1
下载: 导出CSV
-
[1] Dhaenens-Flipo C. Spatial decomposition for a multifacility production and distribution problem[J]. International Journal of Production Economics, 2000, 64 (1/2/3): 177-186. [2] Melkote S, Daskin MS. An integrated model of facility location and transportation network design[J]. Transportation Research Part A, 2001, 35 (6): 515-538. [3] Goetschalckx M, Vidal C J. Dogan K. Modeling and design of global logistics systems: a review of integrated strategic and tactical models and design algorithms[J]. European Journal of Operational Research, 2002, 143 (1): 1-18. doi: 10.1016/S0377-2217(02)00142-X [4] Hwang HS. Design of supply-chain logistics system considering service level[J]. Computers and Industrial Engineering, 2002, 43 (1/2): 283-297. [5] Wu T H, Low C, Bai J W. Heuristic solutions to multi-depot location-routing problems[J]. Computers and Operations Research, 2002, 29 (10): 1 393-1 415. doi: 10.1016/S0305-0548(01)00038-7 [6] SyamS S. A model and methodologies for the location problem with logistical components[J]. Computers and Operations Research, 2002, 29 (9): 1 173-1 193. [7] Amiri A. Designing a distribution network in a supply chain system[J]. European Journal of Operational Research, 2004, 171 (2): 567-576. [8] Gena M, Syarif A. Hybrid genetic algorithm for multi-time period production/distribution planning[J]. Computers and Industrial Engineering, 2005, 48 (4): 799-809. doi: 10.1016/j.cie.2004.12.012 [9] 王丰元, 潘福全, 张丽霞, 等. 基于交通限制的路网最优路径算法[J]. 交通运输工程学报, 2005, 5 (1): 92-95. http://transport.chd.edu.cn/article/id/200501022Wang Feng-yuan, Pan Fu-quan, Zhang Li-xia, et al. Optimal path algorithm of road network with traffic restriction[J]. Journal of Traffic and Transportation Engineering, 2005, 5 (1): 92-95. (in Chinese) http://transport.chd.edu.cn/article/id/200501022 -
点击查看大图
图(3) / 表(2)
计量
- 文章访问数: 367
- HTML全文浏览量: 147
- PDF下载量: 330
- 被引次数: 0
