路网最优费率的双层规划模型及算法

黄亚飞; 刘涛

路网最优费率的双层规划模型及算法

黄亚飞^1,,
刘涛²

1.
长沙理工大学电气与信息工程学院, 湖南长沙 410076
2.
长沙理工大学数学与计算科学学院, 湖南长沙 410076

基金项目:

国家西部交通建设科技项目 2003 318 492 35

详细信息

作者简介:
黄亚飞(1975-), 男, 湖南郴州人, 长沙理工大学讲师, 从事系统优化及智能交通系统研究

中图分类号: U491.13
计量
- 文章访问数: 298
- HTML全文浏览量: 94
- PDF下载量: 438
- 被引次数: 0
出版历程
- 收稿日期: 2006-07-21
- 刊出日期: 2006-12-25

Bi-level programming model and algorithm of optimal toll rate for highway network

HUANG Ya-fei^1
,,
LIU Tao²

1.
School of Electric and Information Engineering, Changsha University of Science and Technology, Changsha 410076, Hunan, China
2.
School of Mathematics and Computational Science, Changsha University of Science and Technology, Changsha 410076, Hunan, China

More Information

Author Bio:
Huang Ya-fei(1975-), male, lecturer, 86-731-8169048, xyrhyh@163.com

摘要

摘要: 为寻求系统、科学的路网最优费率测算方法, 提出用双层规划模型描述路网管理者、收费道路经营者和车辆用户三者在费率决策中的博弈关系, 其中上层以路网用户盈余最大化为目标, 下层是弹性需求下的多车型随机用户均衡模型, 设计了遗传-模拟退火混合优化的求解算法。计算发现路网收费收入目标的高低将直接影响测算所得费率的高低, 进而影响各车型OD出行量, 且时间价值低的车型用户比时间价值高的车型用户受费率变化的影响要更为显著, 表明双层模型在费率决策过程中能兼顾相关各方的利益, 建模时考虑车型分类能更合理地反映现实情况; 与遗传算法、模拟退火算法相比, 遗传-模拟退火算法计算结果最优。
- 交通工程 /
- 收费费率 /
- 随机用户平衡 /
- 弹性需求 /
- 遗传算法 /
- 模拟退火
Abstract: In order to find system and science method to calculate the optimal toll rate of highway network, a bi-level programming model to determine the optimal toll rate was put forward, the relationship among highway network managers, toll road operators and users was described.Its upper objective function was consumer surplus which should be maximized, its lower-level problem was multi-vehicle-type stochastic user equilibrium model with elastic demand.A kind of hybrid optimization algorithm combined genetic algorithm and simulated annealing to solve it was proposed.Calculation result shows that the value of revenue for highway network influences the toll rate directly, furthermore, it influences OD traffic flows, and the influence on the vehicle types with low time value is more obvious than on the vehicle types with high time value, which indicates that the model can balance the benefits among managers, operators and users reasonably, and reflect the fact more accurately when considering vehicle types; compared with genetic algorithm and simulated annealing algorithm, the computation result of the algorithm for the model is least, the algorithm is feasible.
- traffic engineering /
- toll rate /
- stochastic user equilibrium /
- elastic demand /
- genetic algorithm /
- simulated annealing

HTML全文

图 1 路网

Figure 1. Highway network

下载: 全尺寸图片幻灯片

表 1 初始输入数据

Table 1. Initialized input data

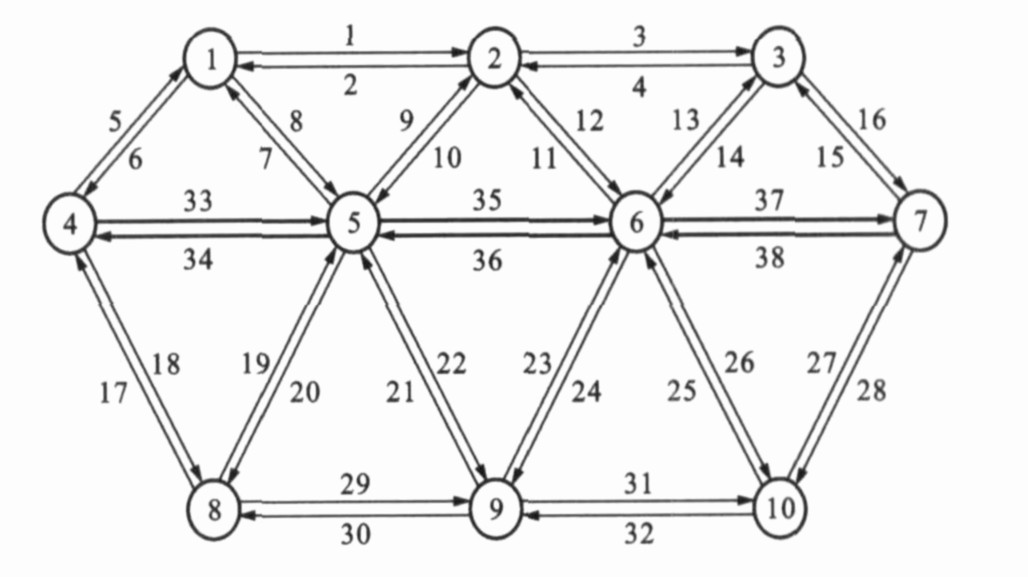
路段	t $_{a}^{0}$ /h	C_amax/ (veh·h^-1)	u_ag/ (HK$·veh^-1)
路段	t $_{a}^{0}$ /h	C_amax/ (veh·h^-1)	客车	货车
1 (2)	2.5	4 000	15.0	40.0
3 (4)	2.5	4 000	15.0	40.0
5 (6)	0.2	6 000	1.2	3.2
7 (8)	0.9	4 000	5.4	14.4
9 (10)	1.1	4 000	6.6	17.6
11 (12)	0.9	4 000	5.4	14.4
13 (14)	0.9	4 000	5.4	14.4
15 (16)	0.2	8 000	1.2	3.2
17 (18)	0.2	8 000	1.2	3.2
19 (20)	0.9	4 000	5.4	14.4
21 (22)	1.0	4 000	6.0	16.0
23 (24)	0.9	4 000	5.4	14.4
25 (26)	1.0	4 000	6.0	16.0
27 (28)	0.2	6 000	1.2	3.2
29 (30)	2.4	3 800	14.4	38.4
31 (32)	2.6	4 200	15.6	41.6
33 (34)	0.7	10 000	4.2	11.2
35 (36)	1.2	16 000	7.2	19.2
37 (38)	0.7	10 000	4.2	11.2

下载: 导出CSV

表 2 路网各OD对的最大潜在交通需求及参数

Table 2. Maximum potential demand of each OD and parameter

OD对	客车 $\bar{q_{r s}^{1}} /$ (veh·h^-1)	货车 $\bar{q_{r s}^{2}} /$ (veh·h^-1)	参数κ_rs
1→3	6 000	2 500	0.25
1→10	6 000	2 500	0.20
3→1	5 400	2 250	0.25
3→8	6 600	2 750	0.20
8→3	6 000	2 500	0.20
8→10	6 000	2 500	0.25
10→1	7 200	3 000	0.20
10→8	4 800	2 000	0.25

下载: 导出CSV

表 3 费率与出行量计算结果

Table 3. Calculation result of toll rates and traffic flows

	预设财务目标		财务目标降低10%		财务目标增加10%		预设目标下推荐费率值
	客车	货车	客车	货车	客车	货车	客车	货车
y₃₃ (y₃₄)	5.12	8.19	4.20	6.72	5.18	8.29	5.00	8.00
y₃₅ (y₃₆)	14.34	22.95	12.11	19.37	14.29	22.86	14.00	23.00
y₃₇ (y₃₈)	6.20	9.92	5.27	8.43	7.33	11.73	6.00	10.00
q₁₃	2 297.52	811.01	2 024.62	799.80	2 142.01	727.95	2 284.00	819.00
q₁₁₀	2 805.67	920.19	2 538.09	950.17	2 805.83	978.15	2 829.00	912.00
q₃₁	2 054.11	642.15	1 800.87	583.09	1 937.11	628.80	2 102.00	665.00
q₃₈	2 997.74	1 062.88	2 707.28	943.28	2 646.41	1 017.83	2 986.00	1 049.00
q₈₃	2 805.36	995.63	2 567.22	954.29	2 512.47	949.76	2 779.00	997.00
q₈₁₀	2 345.30	698.64	2 105.39	707.91	2 433.30	563.46	2 351.00	692.00
q₁₀₁	3 254.51	1 045.91	2 935.04	1 135.36	3 014.69	1 177.24	3 269.00	1 044.00
q₁₀₈	1 740.63	581.77	1 519.24	615.50	1 629.39	647.02	1 753.00	590.00
收费收入V	391 108.16		316 340.52		378 426.91		395 692.00
上层F	-2 673 993.62		-2 684 736.15		-2 666 564.50		-2 671 487.93

下载: 导出CSV

表 4 收费路段流量值

Table 4. Flow calculation result of toll links veh·h^-1

	SUE, θ=0.1		SUE, θ=1.5		SUE, θ=5.0		UE
	客车	货车	客车	货车	客车	货车	客车	货车
x₃₃	3 833.47	1 072.73	4 993.54	1 367.15	6 123.90	2 456.64	6 197.65	2 402.75
x₃₄	3 367.70	1 226.17	4 166.77	1 636.04	6 311.49	2 334.22	6 269.29	2 432.76
x₃₅	4 639.72	1 771.79	5 798.27	1 564.92	9 454.16	4 596.44	10 438.89	4 616.41
x₃₆	4 496.61	1 786.90	5 711.34	1 999.43	9 347.67	4 547.64	10 566.92	4 670.00
x₃₇	4 400.01	1 589.96	3 462.90	1 340.53	4 777.06	2 786.19	6 203.17	2 498.24
x₃₈	3 358.04	1 271.84	4 636.51	928.92	5 176.22	2 720.67	6 276.03	2 529.15

下载: 导出CSV

表 5 求解算法性能比较

Table 5. Performance comparison of algorithms

算法	达到最优解的进化代数	达到最优解执行时间/s	收费纯收入值/HK$	上层目标函数值F
GA	87	1 610.69	352 698.41	-2 662 891.85
SA	100	2 855.12	356 757.42	-2 666 773.89
GASA	36	945.37	391 108.16	-2 673 993.62

下载: 导出CSV

参考文献(12)

[1]	杨兆升, 杨志宏, 赵丹华. 长平高速公路最优收费标准制定方法[J]. 交通运输工程学报, 2003, 3(1): 57-61. doi: 10.3321/j.issn:1671-1637.2003.01.013 Yang Zhao-sheng, Yang Zhi-hong, Zhao Dan-hua. Optimal toll standard in Chang-ping freeway[J]. Journal of Traffic and Transportation Engineering, 2003, 3(1): 57-61. (in Chinese) doi: 10.3321/j.issn:1671-1637.2003.01.013
[2]	陆正峰. 收费高速公路最优收费费率的研究[J]. 西安公路交通大学学报, 1997, 17(3): 105-108 https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL703.023.htm Lu Zheng-feng.Study on toll freeway's optimal toll rate[J]. Journal of Xi'an Highway University, 1997, 17(3): 105-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL703.023.htm
[3]	Yang Hai, Zhang Xiao-ning, Meng Qiang. Modeling private highways in networks with entry-exit based toll charges[J]. Transportation Research Part B, 2004, 38(3): 191-213.
[4]	陈宽民, 罗小强. 城市快速轨道交通合理票价的博弈分析[J]. 长安大学学报: 自然科学版, 2005, 25(4): 52-55. doi: 10.3321/j.issn:1671-8879.2005.04.013 Chen Kuan-min, Luo Xiao-qiang. Game-theory of reasonable ticket price for urban railway transport[J]. Journal of Chang'an University: Natural Science Edition, 2005, 25(4): 52-55. (in Chinese) doi: 10.3321/j.issn:1671-8879.2005.04.013
[5]	李志纯, 谷强, 史峰. 弹性需求下拥挤道路收费的模型与算法研究[J]. 交通运输工程学报, 2001, 1(3): 81-85. doi: 10.3321/j.issn:1671-1637.2001.03.020 Li Zhi-chun, Gu Qiang, Shi Feng. Toll model and algorithm of road jammed with traffic based on elastic demand[J]. Journal of Traffic and Transportation Engineering, 2001, 1(3): 81-85. (in Chinese) doi: 10.3321/j.issn:1671-1637.2001.03.020
[6]	李志纯, 黄海军. 弹性需求下的组合出行模型与求解算法[J]. 中国公路学报, 2005, 18(3): 94-98. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200503020.htm Li Zhi-chun, Huang Hai-jun. Model and solution algorithm with combined travel under elastic demand[J]. China Journal of Highway and Transport, 2005, 18(3): 94-98. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200503020.htm
[7]	刘伟铭. 道路收费系统的优化模型及算法[M]. 北京: 人民交通出版社, 2005.
[8]	Yang Hai. Heuristic algorithm for the bilevel origin-destination matrix estimation problem[J]. Transportation Research Part B, 1995, 29(5): 231-242.
[9]	刘灿齐. 现代交通规划学[M]. 北京: 人民交通出版社, 2001.
[10]	Yang Hai, Yagar S. Traffic assignment and traffic control in general freeway-arterial corridor systems[J]. Transportation Research Part B, 1994, 28(4): 463-486.
[11]	Lundy M, Mees A. Convergence of an annealing algorithm[J]. Mathematical Programming, 1986, 34(1): 111-124.
[12]	刘伟铭, 姜山. 基于GASA混合优化策略的双层规划模型求解算法研究[J]. 土木工程学报, 2003, 36(7): 27-32. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200307005.htm Liu Wei-ming, Jiang Shan. GASA hybrid optimization strategy for bilevel programming models[J]. China Civil Engineering Journal, 2003, 36(7): 27-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200307005.htm