3-D thermal stress computation method of highway concrete box-girder
Article Text (Baidu Translation)
-
摘要: 为了提高混凝土箱梁三维温度应力计算精度, 考虑了泊松效应所引起的各温度应力分量之间的相互耦合关系, 提出了一种基于热弹性理论的温度应力计算方法, 运用简单的结构力学方法实现三维温度应力的空间分析, 导出了混凝土箱梁三维温度应力的实用计算公式。实例计算表明该方法和实用计算公式有效, 箱梁温度应力计算结果与三维有限元分析结果吻合很好, 而传统的温度应力计算方法计算结果偏低, 误差可达25%以上。Abstract: In order to improve the computation precision of 3-D thermal stress of concrete box-girder, the coupling relationship among thermal stress components caused by the effect of Poisson's ratio was taken into account, a computation method of thermal stress was proposed based on the theory of thermoelasticity, an integral property of thermal stress was deduced and used to effectively simplify the computation formulation of thermal stress, thermal stress was analyzed by simple structural analysis method, its practical computation formulas were derived. The results calculated by the method and formulas agree with those calculated by 3-D FEM, while the computation errors of conventional methods are more than 25%, which indicates the method and formulas are feasible.
-
Key words:
- bridge engineering /
- concrete box-girder /
- thermal stress /
- thermoelasticity theory /
- Poisson's ratio
-
表 1 温度应力计算结果对比
Table 1. Comparison of thermal stress computation results
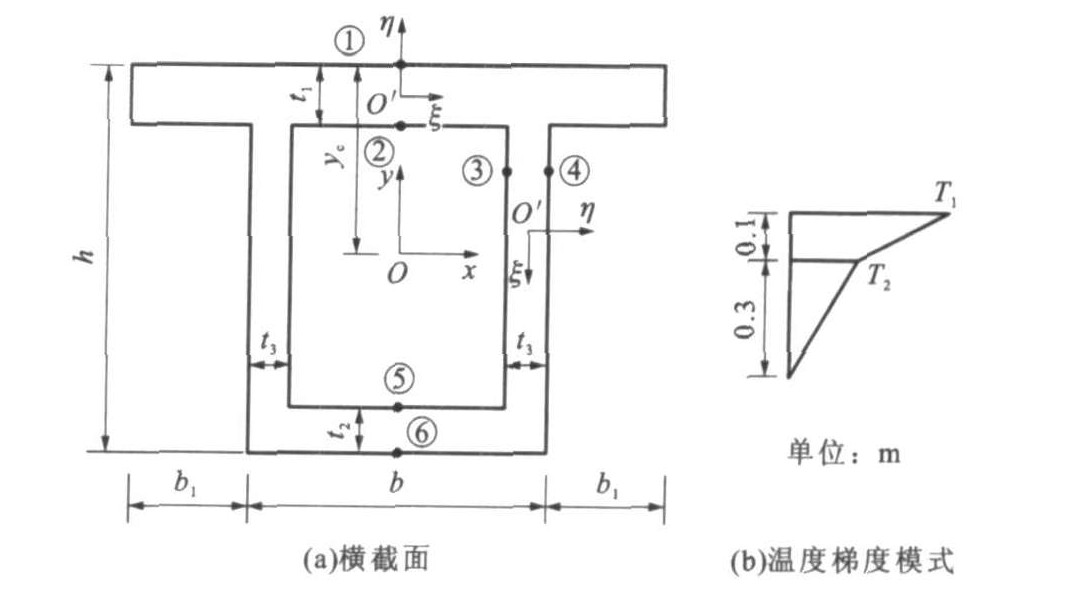
MPa 点号 方法1:三维有限元法 方法2:平面有限元法和式(16) 方法3:公式(20)~(32) σx σy σz σx σy σz σx σy σz ① -6.43 0.00 -7.12 -6.43 0.00 -7.13 -6.40 0.00 -7.10 ② 2.11 0.00 1.97 2.11 0.00 1.97 2.06 0.00 1.97 ③ 0.01 1.30 2.30 0.01 1.30 2.31 0.00 1.43 2.35 ④ 0.00 -1.49 1.74 0.00 -1.49 1.74 0.00 -1.43 1.77 ⑤ -0.06 0.00 -0.30 -0.06 0.00 -0.30 -0.05 0.00 -0.30 ⑥ -0.06 0.00 -0.64 -0.06 0.00 -0.64 -0.04 0.00 -0.64 -
[1] 张玥, 胡兆同, 贾润中. 钢筋混凝土连续弯箱梁桥的温度梯度[J]. 长安大学学报: 自然科学版, 2006, 26(4): 58-62. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604013.htmZhang Yue, Hu Zhao-tong, Jia Run-zhong. Temperature gradient of RCcontinuous curved box girder bridge[J]. Journal of Chang an University: Natural Science Edition, 2006, 26(4): 58-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604013.htm [2] 彭友松, 强士中, 李松. 哑铃形钢管混凝土拱日照温度分布研究[J]. 中国铁道科学, 2006, 27(5): 71-75. doi: 10.3321/j.issn:1001-4632.2006.05.013Peng You-song, Qiang Shi-zhong, Li Song. Temperature distributions in dumbbell cross section concrete-filled steel tube arches due to solar radiation[J]. China Rail way Science, 2006, 27(5): 71-75. (in Chinese) doi: 10.3321/j.issn:1001-4632.2006.05.013 [3] 彭友松, 强士中, 李松. 圆形空心墩日照温度效应分析[J]. 桥梁建设, 2006, 36(4): 74-77. doi: 10.3969/j.issn.1003-4722.2006.04.022Peng You-song, Qiang Shi-zhong, Li Song. Analysis of sun-shine thermal effect of cylindrical concrete hollow pier[J]. Bridge Construction, 2006, 36(4): 74-77. (in Chinese) doi: 10.3969/j.issn.1003-4722.2006.04.022 [4] 张湧, 刘斌, 贺拴海, 等. 桥梁大体积混凝土温度控制与防裂[J]. 长安大学学报: 自然科学版, 2006, 26(3): 43-46. doi: 10.3321/j.issn:1671-8879.2006.03.011Zhang Yong, Liu Bin, He Shuan-hai, et al. Temperature control and anti-crack of massive concreteinlarge bridges[J]. Journal of Chang an University: Natural Science Edition, 2006, 26(3): 43-46. (in Chinese) doi: 10.3321/j.issn:1671-8879.2006.03.011 [5] 徐庆元, 王平, 屈晓晖. 高速铁路桥上无缝线路断轨力计算模型[J]. 交通运输工程学报, 2006, 6(3): 23-26. doi: 10.3321/j.issn:1671-1637.2006.03.006Xu Qing-yuan, Wang Ping, Qu Xiao-hui. Computation model of rupture force between continuously welded rail and high-speed rail way bridge[J]. Journal of Traffic and Transportation Engineering, 2006, 6(3): 23-26. (in Chinese) doi: 10.3321/j.issn:1671-1637.2006.03.006 [6] 陈拴发, 郑木莲, 杨斌, 等. 破裂水泥混凝土路面板沥青加铺层温度应力影响因素[J]. 交通运输工程学报, 2005, 5(3): 25-30. doi: 10.3321/j.issn:1671-1637.2005.03.006Chen Shuan-fa, Zheng Mu-lian, Yang Bin, et al. Thermal stress influence factors of asphalt overlay on cement concrete pavement cracking slab[J]. Journal of Traffic and Transportation Engineering, 2005, 5(3): 25-30. (in Chinese) doi: 10.3321/j.issn:1671-1637.2005.03.006 [7] Elbadry M M, Ghali A. Temperature variations in concrete bridges[J]. Journal of Structural Engineering, 1983, 109(10): 2355-2374. [8] 刘兴法. 混凝土结构的温度应力分析[M]. 北京: 人民交通出版社, 1991. [9] 张元海, 李乔. 桥梁结构日照温差二次力及温度应力计算方法研究[J]. 中国公路学报, 2004, 17(1): 49-52. doi: 10.3321/j.issn:1001-7372.2004.01.011Zhang Yuan-hai, Li Qiao. Study of the methodfor calculation of the thermal stress and secondary force of bridge structure by solar radiation[J]. China Journal of Highway and Transport, 2004, 17(1): 49-52. (in Chinese) doi: 10.3321/j.issn:1001-7372.2004.01.011 [10] 刘来君, 贺拴海, 宋一凡. 大跨径桥梁施工控制温度应力分析[J]. 中国公路学报, 2004, 17(1): 53-56. doi: 10.3321/j.issn:1001-7372.2004.01.012Liu Lai-jun, He Shuan-hai, Song Yi-fan. Analysis of temperature stress in control of long-span bridge construction[J]. China Journal of Highway and Transport, 2004, 17(1): 53-56. (in Chinese) doi: 10.3321/j.issn:1001-7372.2004.01.012 [11] JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. [12] JTG D60-2004, 公路桥涵设计通用规范[S]. [13] Ti moshenko S P, Goodier J N. Theory of Elasticity[M]. New York: The McGraw-Hill Companies, Inc., 1970. -





 下载:
下载: