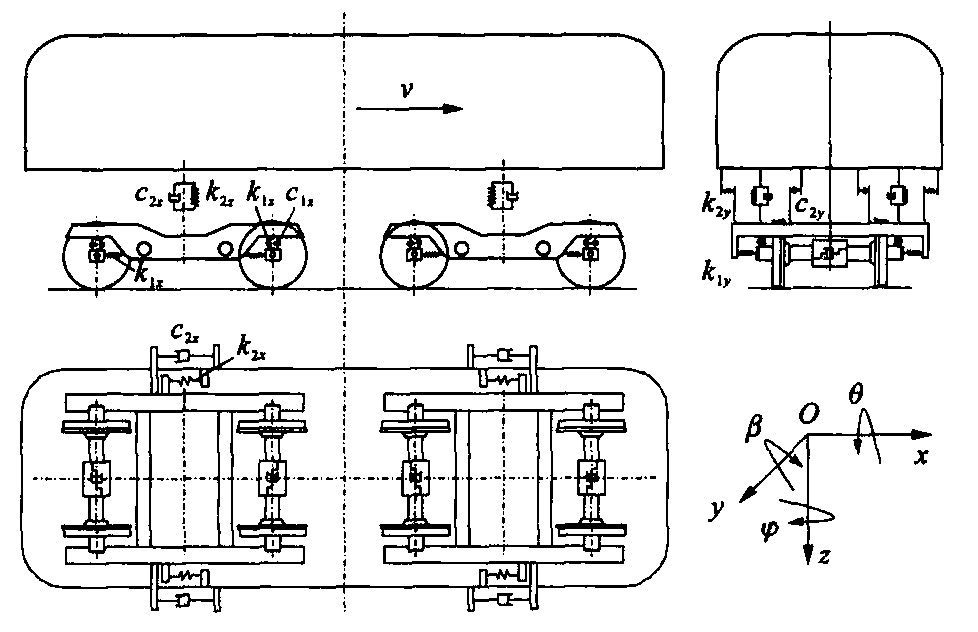
Influence of primary longitudinal position clearance on lateral dynamics of vehicle with MRF coupled wheelsets
Article Text (Baidu Translation)
-
摘要: 为了合理控制车辆轮对定位间隙, 提高磁流变耦合轮对车辆在高速时的横向动力学性能, 建立该车辆的空间动力学模型, 分析了轮对纵向定位间隙对车辆临界速度和曲线通过性能的影响。得出了纵向定位间隙的增大能使磁流变耦合轮对车辆的临界速度急剧下降, 轮对横移量和冲角、轮轨横向力和车体横移加速度快速增大; 只有在小间隙的条件下, 车辆在高速铁路上才具有较高的临界速度和较好的曲线通过性能。Abstract: In order to reasonably control the position clearance of vehicle wheelsets, improve the lateral dynamics performances of vehicle with magneto-rheological fluid (MRF) coupled wheelsets at high speed, a spatial dynamics model of vehicle was established, and the longitudinal position clearance influence of vehicle wheelsets on the critical velocity and curve passing performances of vehicle were analyzed.Analysis result shows that the clearance increase can make vehicle critical velocity descend sharply, make the lateral displacement and attack angle of wheelsets, the lateral force of wheel/rail and lateral acceleration of carbody largen rapidly; vehicle has higher critical velocity and better curve passing performances only in the condition of small clearance.
-
Key words:
- vehicle engineering /
- position clearance /
- coupled wheelsets /
- MRF /
- lateral dynamics
-
图 4 间隙对磁流变耦合轮对车辆曲线通过性能影响
Figure 4. Clearance influence on curve passing properties of vheicle with MRF coupled wheelsets
-
[1] 孙渝麟. 控制209T型转向架轴箱定位间隙的建议[J]. 铁道车辆, 2001, 39 (4): 38-39. https://www.cnki.com.cn/Article/CJFDTOTAL-TDCL200104015.htmSun Yu-lin. Suggest on controlling axlebox position clearance in 209 Tbogies[J]. Rolling Stock, 2001, 39 (4): 38-39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDCL200104015.htm [2] 张晓晖. 209 T型转向架弹性定位套脱落的原因及防范措施[J]. 铁道车辆, 2001, 39 (9): 36-37. https://www.cnki.com.cn/Article/CJFDTOTAL-TDCL202011016.htmZhang Xiao-hui. Analysis on cause of falling off resilient locating buskin 209 Tbogies and preventative measures[J]. Rolling Stock, 2001, 39 (9): 36-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDCL202011016.htm [3] 池茂儒. 磁流变耦合轮对动力学研究[D]. 成都: 西南交通大学, 2003. [4] 池茂儒, 王开文, 傅茂海, 等. 后轮对独立回转新型转向架轮轨横向力的分析[J]. 交通运输工程学报, 2002, 2 (2): 32-35. http://transport.chd.edu.cn/article/id/200202008Chi Mao-ru, Wang Kai-wen, Fu Mao-hai, et al. Analysis on wheel-rail lateral force of the bogie with independently rotating wheels for rear wheelsets[J]. Journal of Traffic and Transportation Engineering, 2002, 2 (2): 32-35. (in Chinese) http://transport.chd.edu.cn/article/id/200202008 [5] 杨岩. 磁流变液离合器的设计与试验分析[D]. 重庆: 重庆大学, 2005. [6] 邢志, 吕建刚, 李猛. 磁流变液特性分析及实验研究[J]. 磁性材料及器件, 2005, 36 (3): 21-23. https://www.cnki.com.cn/Article/CJFDTOTAL-CXCQ200503006.htmXing Zhi, Lu Jian-gang, Li Meng. Behavior analysis and experimental research on magnet-orheological fluids[J]. Journalof Magnetic Materials and Devices, 2005, 36 (3): 21-23. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CXCQ200503006.htm [7] 侯保林, 王炅, Goncalves F D. 一种磁流变阻尼器非参数模型[J]. 南京理工大学学报, 2005, 29 (5): 560-564. doi: 10.3969/j.issn.1005-9830.2005.05.015Hou Bao-lin, Wang Jiong, Goncalves F D. Non-paramrtric model for magneto-rheological damper[J]. Journal of Nanjing University of Science and Technology, 2005, 29 (5): 560-564. (in Chinese) doi: 10.3969/j.issn.1005-9830.2005.05.015 [8] 张峰. 磁流变抛光技术的研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2000. [9] 彭小强. 确定性磁流变抛光的关键技术研究[D]. 长沙: 国防科技大学, 2004. [10] 司鹄. 磁流变体的力学机理研究[D]. 重庆: 重庆大学, 2003. [11] 蒋建东, 梁锡昌, 王光建. 磁流变离合器及恒矩器的研究[J]. 机械科学与技术, 2005, 24 (4): 431-433. https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX20050400F.htmJiang Jian-dong, Liang Xi-chang, Wang Guang-jian. Study of a magneto-rheological fluid cluch and torque-converter[J]. Mechanical Science and Technology, 2005, 24 (4): 431-433. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX20050400F.htm -
下载:
点击查看大图
图(5)
计量
- 文章访问数: 497
- HTML全文浏览量: 166
- PDF下载量: 238
- 被引次数: 0
