Permafrost subgrade deformation forecast based on phase space reconstruction and partial least squares regression
-
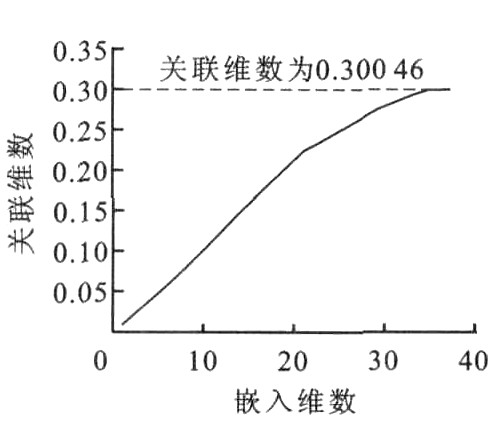
摘要: 为了正确预测多年冻土路基变形, 将多年冻土路基变形单变量混沌时间序列进行相空间重构, 依重构空间嵌入维数38在多维空间中定义自变量、因变量和样本数, 利用偏最小二乘法对所构造的自变量进行主成分提取, 建立路基变形预测模型, 借助多种评判指标进行模型精度分析, 并绘制了预测值与实测值散点图。对比分析结果表明所有样本点都集中在散点图对角线附近, 相关系数达0.889 4, 预测值与实测值最大相对误差为9.75%, 说明建立的预测模型合理可信, 利用该预测模型进行多年冻土路基变形预测可行。Abstract: In order to accurately forecast permafrost subgrade deformation, a single variable chaos time series of permafrost subgrade deformation was constructed in multidimensional phase space, some independent variables, function and sample numbers were defined according to embeded 38 dimensions of the space, the main components of independent variables were picked by using partial least squares regression method, a deformation forecast model was constructed, the precision of the model was analyzed by recurring multiplicate evaluation indices, and the comparative figure between forecast values and measure values was plotted.Analysis result shows that all sample points concentrate near the diagonal line of the figure, their correlation index is 0.889 4, their maximum relative error is 9.75%, which indicates that the model is reasonable and credible, can forecast subgrade deformation in permafrost regions.
-
图 1 关联维数与嵌入维数的关系曲线
Figure 1. Correlation curve of correlation dimension and embedding dimension
表 1 计算结果
Table 1. Calculation result
n t1 t2 u1 1 1.3611 -0.2650 2.1092 2 0.1195 -0.5051 0.2194 3 0.0155 -0.1672 0.7593 4 0.7539 -1.5961 0.7593 5 0.5757 1.8262 0.7593 6 -3.1605 0.4499 -3.5603 7 -0.0422 2.4845 -0.0506 8 -0.1750 1.8028 1.0293 9 2.9960 3.2630 4.8090 10 -3.9405 -1.8117 -5.9900 11 -0.2059 0.5387 0.4894 12 -0.0820 -2.9473 -0.5851 13 1.4593 -4.9033 -0.5851 14 1.0862 -0.3122 2.1092 15 -3.2377 -1.3539 -3.2903 16 2.6411 -0.4473 2.1092 17 -2.1337 -1.7324 -2.2104 18 1.0695 -1.2313 -0.0506 19 -1.5002 1.1623 -1.1305 20 -1.6382 3.5111 -0.0506 21 0.7788 -0.6139 0.4894 22 0.6907 1.0541 0.4894 23 2.0650 1.3081 2.6492 24 -1.7810 0.5877 -0.5851 25 0.0494 -0.8479 -0.5851 26 1.5876 -2.3886 -0.5851 27 1.3778 -0.0507 1.5693 28 0.4181 1.2514 1.0293 29 -2.4137 1.2406 -1.6704 30 1.8768 -0.9613 1.5693 31 0.3529 0.9405 -0.0506 32 -1.2449 0.5939 -1.6704 33 -0.3411 1.8492 0.4894 34 -0.8902 1.2532 -0.5851 35 1.2227 -1.3645 1.0293 36 0.0972 0.8040 1.0293 37 -2.3028 -2.2597 -3.2903 38 2.4942 -0.1620 1.0293 均值 0.0000 0.0000 0.0000 方差 2.8870 3.0000 3.7960 
下载: 导出CSV
表 2 预测结果
Table 2. Forecast result
时间序列编号 预测值/cm 时间序列编号 预测值/cm 时间序列编号 预测值/cm 1 -0.5332 9 0.5222 17 -0.1168 2 0.4763 10 -0.2067 18 0.2494 3 -0.4522 11 0.7851 19 0.5545 4 0.3624 12 -0.1399 20 -0.0926 5 -0.0077 13 0.2018 21 0.0825 6 -0.1577 14 0.1399 22 0.0994 7 0.6635 15 0.2879 23 -0.2929 8 -0.5587 16 0.1251 24 0.7716
下载: 导出CSV
-
[1] 王铁行. 多年冻土地区路基冻胀变形分析[J]. 中国公路学报, 2005, 18 (2): 1-5. doi: 10.3321/j.issn:1001-7372.2005.02.001Wang Tie-hang. Analysis of frost heave on subgradein permafrost regions[J]. China Journal of Highway and Transport, 2005, 18 (2): 1-5. (in Chinese) doi: 10.3321/j.issn:1001-7372.2005.02.001 [2] 汪海年, 窦明健. 青藏高原多年冻土区路基温度场数值模拟[J]. 长安大学学报: 自然科学版, 2006, 26 (4): 11-15. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604003.htmWang Hai-nian, Dou Ming-jian. Numerical simulation of thermal field in permafrost embankments of Qinghai-Tibethighway[J]. Journal of Chang'an University: Natural Science Edition, 2006, 26 (4): 11-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604003.htm [3] 汪双杰, 陈建兵, 黄晓明. 热棒路基降温效应的数值模拟[J]. 交通运输工程学报, 2005, 5 (3): 41-46. http://transport.chd.edu.cn/article/id/200503009Wang Shuang-jie, Chen Jian-bing, Huang Xiao-ming. Numerical simulation of cooling effect for heat pipe subgrade[J]. Journal of Traffic and Transportation Engineering, 2005, 5 (3): 41-46. (in Chinese) http://transport.chd.edu.cn/article/id/200503009 [4] 毛雪松, 李宁, 王秉纲. 多年冻土路基水-热-力耦合理论模型及数值模拟[J]. 长安大学学报: 自然科学版, 2006, 26 (4): 16-19. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604004.htmMao Xue-song, Li Ning, Wang Bing-gang. Coupling modeland numerical simulation of moisture-heat-stress fieldsin permafrost embankment[J]. Journal of Chang'an University: Natural Science Edition, 2006, 26 (4): 16-19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604004.htm [5] 吕金虎, 陆君安, 陈士华. 混沌时间序列分析及应用[M]. 武汉: 武汉大学出版社, 2002. [6] 周创兵, 陈益峰. 基于相空间重构的边坡位移预测[J]. 岩土力学, 2000, 21 (3): 205-208. doi: 10.3969/j.issn.1000-7598.2000.03.004Zhou Chuang-bing, Chen Yi-feng. Application of phase spacere construction in slope displacement forecasting[J]. Rock andSoil Mechanics, 2000, 21 (3): 205-208. (in Chinese) doi: 10.3969/j.issn.1000-7598.2000.03.004 [7] 王惠文. 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社, 1999. [8] 汪双杰. 高原多年冻土区公路路基稳定及预测技术研究[D]. 南京: 东南大学, 2005. [9] 侯曙光, 汪双杰, 黄晓明. 基于相空间重构的冻土路基变形预测[J]. 交通运输工程学报, 2005, 5 (2): 35-37. http://transport.chd.edu.cn/article/id/200502009Hou Shu-guang, Wang Shuang-jie, Huang Xiao-ming. Sub-grade deformation forecast of frozen soil based on phase spacere construction[J]. Journal of Traffic and Transportation Engineering, 2005, 5 (2): 35-37. (in Chinese) http://transport.chd.edu.cn/article/id/200502009 [10] 侯曙光. 多年冻土路基融沉机理及路面结构对策研究[D]. 南京: 东南大学, 2006. -
点击查看大图
图(8) / 表(2)
计量
- 文章访问数: 270
- HTML全文浏览量: 128
- PDF下载量: 351
- 被引次数: 0
