Computation model of lateral collision rate on parallel routesbased on VOR navigation
Article Text (Baidu Translation)
-
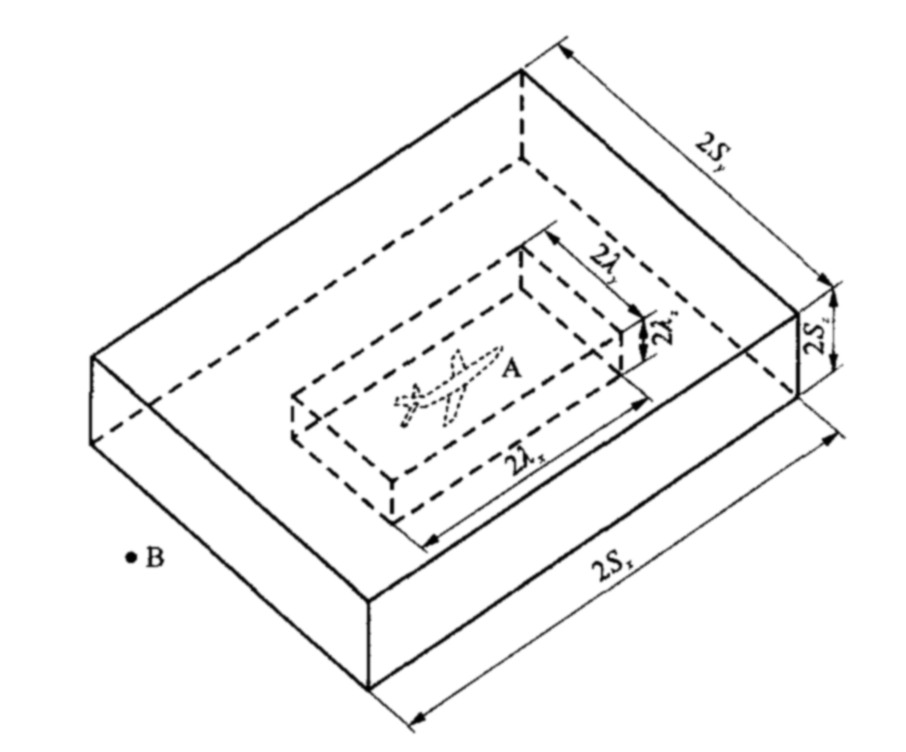
摘要: 为了有效确定平行航路安全间隔与评估碰撞风险, 分析了侧向碰撞影响因素, 利用Reich模型和概率论理论, 建立了非洋区VOR导航下平行航路的侧向碰撞率计算模型。对Reich模型进行了改进, 以圆柱体碰撞模板代替传统的长方体碰撞模板, 推导出平行航路侧向碰撞率的计算公式, 利用事件的概率运算法则, 给出VOR导航下航路飞行时两机侧向重叠概率的计算模型。计算结果表明: 给定航路侧向碰撞率小于规定值, 所设定的平行航路间隔在给定的飞行环境下是安全的, 符合客观实际, 因此计算模型可行。Abstract: In order to effectively confirm the safe separation of parallel routes and evaluate collision risk, lateral collision influence factors were analyzed, Reich model and probability theory were introduced, and a computation model of lateral collision rate on parallel routes was established based on VOR navigation in continental areas. The Reich model was improved, a computation formula of lateral collision rate was deduced according to column collision slab instead of cuboid collision slab, and a computation model of lateral overlapping rate between two aircrafts was given according to event probability operation principle. Computation result shows that the computation value of lateral collision rate on gave parallel routes is less than normal value, the flight environment with gave separations is safe, which accords with real condition, so the model is feasible.
-
[1] Filkins L D, Little J W. Study of aircraft separation criteria[D]. Michigan: University of Michigan, 1964. [2] 王欣, 徐肖豪. 空中飞机侧向间隔标准的初步研究[J]. 中国民航学院学报, 2001, 19(1): 1-5. doi: 10.3969/j.issn.1001-5590.2001.01.001Wang Xin, Xu Xiao-hao. Study of lateral separation in air traffic control[J]. Journal of Aviation University of China, 2001, 19(1): 1-5. (in Chinese) doi: 10.3969/j.issn.1001-5590.2001.01.001 [3] 应爱玲, 徐肖豪. 空域飞行侧向碰撞危险的Reich模型方法研究[J]. 中国民航学院学报, 2002, 20(4): 6-10. doi: 10.3969/j.issn.1001-5590.2002.04.002Ying Ai-ling, Xu Xiao-hao. Reich model in collision risk study of airspace flight[J]. Journal of Civil Aviation University of China, 2002, 20(4): 6-10. (in Chinese) doi: 10.3969/j.issn.1001-5590.2002.04.002 [4] 朱代武. 低空空域飞行冲突避让算法[J]. 交通运输工程学报, 2005, 5(3): 73-76. doi: 10.3321/j.issn:1671-1637.2005.03.016Zhu Dai-wu. Calculational methods of avoiding flight conflict in lowaltitude airspace[J]. Journal of Traffic and Transportation Engineering, 2005, 5(3): 73-76. (in Chinese) doi: 10.3321/j.issn:1671-1637.2005.03.016 [5] 徐杰, 杜文, 孙宏. 跟随车安全距离的分析[J]. 交通运输工程学报, 2002, 2(1): 101-104. http://transport.chd.edu.cn/article/id/200201022Xu Jie, Du Wen, Sun Hong. Safety distance about car-following[J]. Journal of Traffic and Transportation Engineering, 2002, 2(1): 101-104. (in Chinese) http://transport.chd.edu.cn/article/id/200201022 [6] 侯志祥, 吴义虎, 刘振闻, 等. 高速公路汽车追尾模型[J]. 交通运输工程学报, 2004, 4(4): 37-39. doi: 10.3321/j.issn:1671-1637.2004.04.010Hou Zhi-xiang, Wu Yi-hu, Liu Zhen-wen, et al. Automobile rear end collision model onfreeway[J]. Journal of Traffic and Transportation Engineering, 2004, 4(4): 37-39. (in Chinese). doi: 10.3321/j.issn:1671-1637.2004.04.010 [7] Reich P G. Analysis of long-range air traffic systems: separation standardsⅠ[J]. Journal of Navigation, 1966, 19(1): 88-98. [8] Hsu D A. The evaluation of aircraft collision probabilities at intersecting air routes[J]. Journal of Navigation, 1981, 34(1): 78-102. [9] 赵洪元. 空中交通安全及几种新型可靠性估计理论[D]. 北京: 北方交通大学, 1997. [10] Anderson D, Lin X G. Collision risk model for a crossing track separation methodology[J]. Journal of Navigation, 1996, 49(3): 337-349. [11] 马子兴. 航管二次雷达间隔的评估分析研究[D]. 天津: 中国民航学院, 2004. -





 下载:
下载: