Trip mode transfer model by simulating quantum jump
-
摘要: 为定量描述出行方式转移规律, 分析了出行方式转移与量子跃迁的相似特性, 根据量子能级跃迁理论建立了出行方式转移模型, 通过分析长春市居民出行调查数据, 推导了出行方式转移的多项式拟合公式, 分别采用2~4次多项式标定了拟合系数, 并且进行了相关性检验。数据验证结果表明: 某种出行方式向其他方式转移时, 距离差与收入差的函数关系符合常数项为0的2次或高次多项式拟合公式; 2次多项式拟合任意出行方式向其他方式转移所得到的复相关系数均在0.900 0以上, 3次或4次多项式拟合所得到的复相关系数均为1.000 0。这证明模拟量子跃迁的出行方式转移模型可以定量描述任意出行方式向其他出行方式转移的规律。Abstract: To quantificationally describe trip mode transfer rules, the comparability between trip mode transfer and quantum jump was analyzed in detail, and a trip mode transfer model was put forward according to quantum energy level jump theory. In order to calibrate the model, the polynomial imitation equation was deduced by analyzing inhabitant trip survey data from Changchun City, the imitation coefficients were ascertained, and their correlative tests were made by using quadratic, cubic and biquadratic polynomials respectively. Data validating result shows that the function relation between distance difference and income balance fits quadratic or higher polynomial whose constant items are zero when one mode transfers to other modes; the correlative coefficients are all more than 0.900 0 when using quadratic polynomial, and they are all 1.000 0 when using cubic or biquadratic polynomial. It is obvious that the model is feasible to quantificationally describe the rules of trip mode transfer.
-
Key words:
- traffic planning /
- inhabitant reorganization /
- quantum jump theory /
- trip mode transfer /
- energy level
-
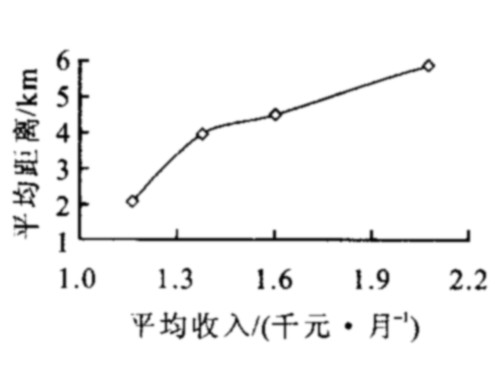
表 1 平均收入与平均距离
Table 1. Average income and average distance
出行方式 自行车 公交车 摩托车 小汽车 平均收入/(千元·月-1) 1.161 6 1.373 4 1.600 0 2.076 0 平均距离/km 2.054 4 3.967 9 4.496 2 5.867 4 表 2 收入差与距离差
Table 2. Income balance and distance balance
出行方式转移 自行车→自行车 自行车→公交车 自行车→摩托车 自行车→小汽车 收入差/(千元·月-1) 0.000 0 0.211 8 0.438 4 0.914 4 距离差/km 0.000 0 1.913 5 2.441 8 3.813 0 出行方式转移 公交车→自行车 公交车→公交车 公交车→摩托车 公交车→小汽车 收入差/(千元·月-1) -0.211 8 0.000 0 0.226 6 0.702 6 距离差/km -1.913 5 0.000 0 0.528 3 1.899 5 出行方式转移 摩托车→自行车 摩托车→公交车 摩托车→摩托车 摩托车→小汽车 收入差/(千元·月-1) -0.438 4 -0.226 6 0.000 0 0.476 0 距离差/km -2.441 8 -0.528 3 0.000 0 1.371 2 出行方式转移 小汽车→自行车 小汽车→公交车 小汽车→摩托车 小汽车→小汽车 收入差/(千元·月-1) -0.914 4 -0.702 6 -0.476 0 0.000 0 距离差/km -3.813 0 -1.899 5 -1.371 2 0.000 0 表 3 某种方式向其他方式转移的多项式拟合
Table 3. Polynomial fitting for one mode transferring to others
自行车出行方式 收入差/(千元·月-1) 统计距离差/km 2次多项式拟合距离差/km 3次多项式拟合距离差/km 4次多项式拟合距离差/km 0.000 0 0.000 0 0.000 0 0.000 0 0.000 0 0.211 8 1.913 5 1.523 8 1.913 5 1.913 5 0.438 4 2.441 8 2.719 7 2.441 8 2.441 8 0.914 4 3.813 0 3.770 0 3.813 0 3.813 0 参数值 — 8.120 2, -4.371 5 13.904 8, -26.717 7, 17.576 0 12.951 1, -18.995 8, 0.000 0, 11.233 6 复相关系数 — 0.984 4 1.000 0 1.000 0 公交车出行方式 -0.211 8 -1.913 5 -1.566 5 -1.913 5 -1.913 5 0.000 0 0.000 0 0.000 0 0.000 0 0.000 0 0.226 6 0.528 3 1.151 3 0.528 3 0.528 3 0.702 6 1.899 5 1.803 2 1.899 5 1.899 5 参数值 — 6.277 6, -5.282 0 4.952 5, -15.549 9, 17.576 0 4.952 5, -15.549 9, 17.576 0, 0.000 0 复相关系数 — 0.964 8 1.000 0 1.000 0 摩托车出行方式 -0.438 4 -2.441 8 -2.240 6 -2.441 8 -2.441 8 -0.226 6 -0.528 3 -1.034 9 -0.528 3 -0.528 3 0.000 0 0.000 0 0.000 0 0.000 0 0.000 0 0.476 0 1.371 2 1.315 3 1.371 2 1.371 2 参数值 — 3.985 4, -2.567 3 0.612 8, -3.601 7, 17.576 0 0.612 8, -3.601 7, 17.576 0, 0.000 0 复相关系数 — 0.979 7 1.000 0 1.000 0 小汽车出行方式 -0.914 4 -3.813 0 -3.671 7 -3.813 0 -3.813 0 -0.702 6 -1.899 5 -2.255 2 -1.899 5 -1.899 5 -0.476 0 -1.371 2 -1.117 6 -1.371 2 -1.371 2 0.000 0 0.000 0 0.000 0 0.000 0 0.000 0 参数值 — 0.537 1, -3.804 0 9.130 9, 21.496 9, 17.576 0 6.562 8, 9.638 3, 0.000 0, -8.397 5 复相关系数 — 0.985 8 1.000 0 1.000 0 -
[1] 王殿海, 李振福. 居民重组与出行分布的复杂问题及研究方法[J]. 交通运输工程与信息学报, 2003, 1(1): 113-117. https://www.cnki.com.cn/Article/CJFDTOTAL-JTGC200301017.htmWang Dian-hai, Li Zhen-fu. A study framework on complex issue of resident reorganizing and trip distribution[J]. Journal of Transportation Engineering and Information, 2003, 1(1): 113-117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JTGC200301017.htm [2] 朱从坤, 王洁, 冯焕焕. 区域运输通道内客运方式分担率模型[J]. 交通运输工程学报, 2005, 5(4): 111-115. http://transport.chd.edu.cn/article/id/200504023Zhu Cong-kun, WangJie, Feng Huan-huan. Models of passenger traffic sharing rates of regional transport corridor[J]. Journal of Traffic and Transportation Engineering, 2005, 5(4): 111-115. (in Chinese) http://transport.chd.edu.cn/article/id/200504023 [3] 李志瑶, 隽志才, 宗芳. 居民出行时间选择及拥挤收费政策[J]. 交通运输工程学报, 2005, 5(3): 105-110. http://transport.chd.edu.cn/article/id/200503022Li Zhi-yao, Juan Zhi-cai, Zong Fang. Resident travel time choice and congestion pricing policy[J]. Journal of Traffic and Transportation Engineering, 2005, 5(3): 105-110. (in Chinese) http://transport.chd.edu.cn/article/id/200503022 [4] 彭辉, 付慧敏. 北京-郑州运输通道内旅客出行的特征[J]. 长安大学学报: 自然科学版, 2005, 25(6): 66-69. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200506015.htmPeng Hui, Fu Hui-min. Travel characteristics in transportation corridor of Beijing-Zhengzhou[J]. Journal of Chang an University: Natural Science Edition, 2005, 25(6): 66-69. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200506015.htm [5] 徐永能, 李旭宏, 朱彦东, 等. 城市居民出行方式选择的满意准则模型[J]. 交通与计算机, 2005, 23(4): 54-57. https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS200504014.htmXu Yong-neng, Li Xu-hong, Zhu Yan-dong, et al. Satisfaction rule model of modal selection of going outside for civilians[J]. Computer and Communications, 2005, 23(4): 54-57. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS200504014.htm [6] 四兵锋, 孙壮志, 赵小梅. 基于随机用户平衡的混合交通网络流量分离模型[J]. 中国公路学报, 2006, 19(1): 93-98. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200601019.htmSi Bing-feng, Sun Zhuang-zhi, Zhao Xiao-mei. Mixed traffic network flow-split model based on stochastic user equilibrium[J]. China Journal of Highway and Transport, 2006, 19(1): 93-98. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200601019.htm [7] 姚荣涵, 王殿海. 居民出行分布的熵模型及其参数标定[J]. 交通运输工程学报, 2005, 5(4): 106-110. http://transport.chd.edu.cn/article/id/200504022Yao Rong-han, Wang Dian-hai. Entropy models of inhabitant trip distributions and parameters calibration[J]. Journal of Traffic and Transportation Engineering, 2005, 5(4): 106-110. (in Chinese) http://transport.chd.edu.cn/article/id/200504022 [8] 高峰, 姚荣涵, 王殿海. 基于Langevin方程的居民分布模型[J]. 吉林大学学报: 工学版, 2005, 35(2): 187-190. https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY20050200H.htmGao Feng, Yao Rong-han, Wang Dian-hai. Inhabitant distribution model based on Langevin equation[J]. Journal of Jilin University: Engineering and Technology Edition, 2005, 35(2): 187-190. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY20050200H.htm [9] 王殿海, 杨兆升, 雷雨龙. 模拟电子云居民分布模型研究[J]. 系统工程理论与实践, 1996, 16(7): 71-74. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL607.012.htmWang Dian-hai, Yang Zhao-sheng, Lei Yu-long. Research on the inhabitants distribution model by simulation electron cloud[J]. Systems Engineering-Theory & Practice, 1996, 16(7): 71-74. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL607.012.htm [10] 曲昭伟, 梁春岩, 王殿海. 基于电子能量的居民出行分布模拟模型研究[J]. 交通运输系统工程与信息, 2003, 3(4): 48-52. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT200304010.htmQu Zhao-wei, Liang Chun-yan, Wang Dian-hai. Research on simulation of inhabitant trip distribution based on electronic energy[J]. Journal of Transportation Systems Engineering and Information Technology, 2003, 3(4): 48-52. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT200304010.htm [11] 周绍森, 范成, 周景. 原子物理学[M]. 上海: 华东师范大学出版社, 1998. -





 下载:
下载: