铁道车辆振动响应特性

池茂儒; 张卫华; 曾京; 戴焕云; 邬平波

铁道车辆振动响应特性

西南交通大学牵引动力国家重点实验室室，四川成都 610031)

基金项目:

国家自然科学基金项目 50705079

国家自然科学杰出青年基金项目 50525518

高等学校科技创新工程重大项目 0705044

详细信息

作者简介:
池茂儒(1973-), 男, 四川通江人, 西南交通大学副研兖员, 工学博士, 从事机车车辆动力学研究

中图分类号: U211.3;U270.1
计量
- 文章访问数: 381
- HTML全文浏览量: 122
- PDF下载量: 597
- 被引次数: 0
出版历程
- 收稿日期: 2007-08-20
- 刊出日期: 2007-10-25

Vibrant response characteristic of railway vehicle

Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, Sichuan, China

More Information

Author Bio:
Chi Mao-ru(1973-), male, EngD, associate researcher, +86-28-87600882, cmr2000@163.com

摘要

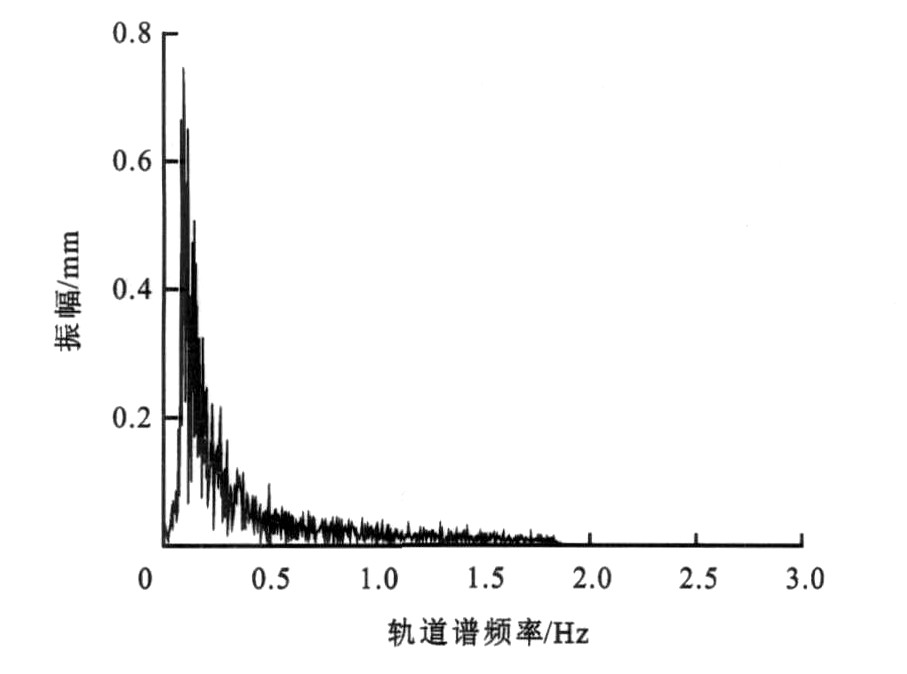
摘要: 为改善车辆的乘坐舒适性, 研究了车辆的振动响应特性, 建立了车辆系统动力学模型, 计算了转向架蛇行运动模态和车体固有振动模态的频域模态参数与车辆在不同速度下的时域平稳性指标。计算结果表明: 转向架蛇行运动频率和轨道激扰主频率随着车辆运行速度的增大而增大, 而车体的固有振动频率是不随速度而变化的; 在某一速度下, 转向架的蛇行运动频率和轨道激扰主频率必然与车体相关振动的固有频率接近而发生共振, 共振会严重恶化车辆的平稳性, 因此, 应采取适当措施使共振速度区远离车辆的常用运行速度, 以保证车辆运行平稳。
- 车辆工程 /
- 转向架 /
- 振动响应 /
- 乘坐舒适性
Abstract: In order to improve the riding comfort of vehicle, the vibrant response characteristic of vehicle was studied, a dynamics model of vehicle system was set up, frequency-domain mode parameters on the hunting mode of bogie and the natural mode of car body were calculated, and stationarity indices of vehicle at the different speeds were computed in time-domain.Computation result shows that the hunting frequency of bogie and the primary frequency of track irregularities increase with the increase of running velocity, but the natural frequency of car body has no change; they must approach the natural frequency of car body and take place resonance at certain speed, and the resonance will badly worsen the riding comfort of vehicle.So in order to improve the comfort, some proper measures should be taken to keep the resonance speed away from the common running speed of vehicle.
- vehicle engineering /
- bogie /
- vibration response /
- riding comfort

HTML全文

图 1 轨道谱

Figure 1. Track irregularity

下载: 全尺寸图片幻灯片

图 2 轨道激扰频率与车辆运行速度的关系

Figure 2. Relationship between track irregularity frequency and running speed of vehicle

下载: 全尺寸图片幻灯片

图 3 车辆系统振动频率图谱

Figure 3. Vibrational Spectrum of vehicle system

下载: 全尺寸图片幻灯片

图 4 振动加速度的变化

Figure 4. Change of vibration acceleration

下载: 全尺寸图片幻灯片

图 5 平稳性指标的变化

Figure 5. Change of ride quality

下载: 全尺寸图片幻灯片

图 6 车辆运行速度为30 km·h^-1时的横向振动加速度

Figure 6. Lateral vibration acceleration of car body at 30 km·h^-1

下载: 全尺寸图片幻灯片

图 7 车辆运行速度为75 km·h^-1时的横向振动加速度

Figure 7. Lateral vibration acceleration of car body at 75 km·h^-1

下载: 全尺寸图片幻灯片

图 8 车辆运行速度为120 km·h^-1时的横向振动加速度

Figure 8. Lateral vibration acceleration of car body at 120 km·h^-1

下载: 全尺寸图片幻灯片

图 9 车辆运行速度为120 km·h^-1时的垂向振动加速度

Figure 9. Vertical vibration acceleration of car body at 120 km·h^-1

下载: 全尺寸图片幻灯片

表 1 自振频率

Table 1. Natural frequencies Hz

下心滚摆	上心滚摆	摇头振动	点头振动	浮沉振动
0.505	1.546	0.642	1.661	1.758

下载: 导出CSV

表 2 转向架蛇行运动频率和轨道激扰谱主频与车辆运行速度的关系

Table 2. Relationship among track irregularity frequency, bogie hunting frequency and vehicle running speed

速度/(km·h^-1)	1	20	40	60	80	100	120	140	160	180	200
蛇行频率/Hz	0.021	0.426	0.847	1.272	1.705	2.140	2.574	3.002	3.41	3.809	4.172
激扰主频/Hz	0.005	0.094	0.188	0.282	0.376	0.470	0.564	0.658	0.752	0.846	0.940

下载: 导出CSV

参考文献(10)

[1]	Frohling R D. Lowfrequency dynamic vehicle/track interaction: modeling and simulation[J]. Vehicle System Dynamics, 1998, 28(Sup): 30-46.
[2]	王开云, 翟婉明, 刘建新, 等. 线路不平顺波长对提速列车横向舒适性影响[J]. 交通运输工程学报, 2007, 7(1): 1-5. doi: 10.3321/j.issn:1671-1637.2007.01.001 Wang Kai-yun, Zhai Wan-ming, Liu Jian-xin, et al. Effect of rail irregularity wavelength on lateral running comfort of speed-raised train[J]. Journal of Traffic and Transportation Engineering, 2007, 7(1): 1-5. (in Chinese) doi: 10.3321/j.issn:1671-1637.2007.01.001
[3]	臧其吉. 铁道车辆动力学性能与轨道条件密切相关[J]. 电力机车与城轨车辆, 2004, 27(1): 4-7. doi: 10.3969/j.issn.1672-1187.2004.01.002 Zang Qi-ji. Track vehicles dynamics performance is related to the conditions of trackage closely[J]. Electric Locomatives and Mass Transit Vehicles, 2004, 27(1): 4-7. (in Chinese) doi: 10.3969/j.issn.1672-1187.2004.01.002
[4]	黄俊飞, 练松良, 宗德明, 等. 轨道随机不平顺与车辆动力响应的相干分析[J]. 同济大学学报: 自然科学版, 2003, 31(1): 16-20. doi: 10.3321/j.issn:0253-374X.2003.01.004 Huang Jun-fei, Lian Song-liang, Zong De-ming, et al. Analysis of coherence between track random irregularity and vehicle dynamic response[J]. Journal of Tongji University: Natural Science, 2003, 31(1): 16-20. (in Chinese) doi: 10.3321/j.issn:0253-374X.2003.01.004
[5]	周劲松, 任利惠, 沈钢. 高速列车运行平稳性研究[J]. 机械科学与技术, 2003, 22(6): 900-903. doi: 10.3321/j.issn:1003-8728.2003.06.012 Zhou Jin-song, Ren Li-hui, Shen Gang. Research on ride quality of high-speed train[J]. Mechanical Science and Technology, 2003, 22(6): 900-903. (in Chinese) doi: 10.3321/j.issn:1003-8728.2003.06.012
[6]	练松良, 黄俊飞. 客货共运线路轨道不平顺不利波长的分析研究[J]. 铁道学报, 2004, 26(2): 111-115. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200402021.htm Lian Song-liang, Huang Jun-fei. Study of the detri mental wavelengths of track irregularities for railway with passenger and freight traffic[J]. Journal of the China Railway Society, 2004, 26(2): 111-115. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200402021.htm
[7]	芦睿泉, 练松良. 轨道复合不平顺对提速列车运行影响的研究[J]. 铁道科学与工程学报, 2005, 2(5): 17-22. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD200505003.htm Lu Rui-quan, Lian Song-liang. Research of the effect of track complex irregularities on the vehicle dynamic response[J]. Journal of Railway Science and Engineering, 2005, 2(5): 17-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD200505003.htm
[8]	张洪. 基于运行模态识别的铁路客车动力学特性研究[D]. 上海: 同济大学, 2005.
[9]	Hermans L, Vender H. Modal testing and analysis of structures under operational conditions[J]. Mechanical Systemsand Signal Processing, 1999, 13(2): 193-216.
[10]	夏江宁, 陈志峰, 宋汉文. 基于动力学环境试验数据的模态参数识别[J]. 振动与冲击, 2006, 25(1): 99-103. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ200601027.htm Xia Jiang-ning, Chen Zhi-feng, Song Han-wen. Modal parameter identification of experimental data based on dynamic environment[J]. Journal of Vibration and Shock, 2006, 25(1): 99-103. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ200601027.htm