沥青路面永久变形的非线性粘弹-弹塑性本构模型

彭妙娟; 许志鸿

沥青路面永久变形的非线性粘弹-弹塑性本构模型

彭妙娟^1,,
许志鸿²

1.
上海大学土木工程系，上海 200072
2.
同济大学交通运输工程学院，上海 200092

基金项目:

国家自然科学基金项目 10571118

详细信息

作者简介:
彭妙娟(1965-)，女，山西稷山人.上海大学副教授，工学博士，从事道路工程研究

中图分类号: U416.217
计量
- 文章访问数: 209
- HTML全文浏览量: 93
- PDF下载量: 692
- 被引次数: 0
出版历程
- 收稿日期: 2007-06-02
- 刊出日期: 2007-10-25

Nonlinear viscoelastic-elastoplastic constitutive model of permanent deformation for asphalt pavement

PENG Miao-juan^1
,,
XU Zhi-hong²

1.
Department of Civil Engineering, Shanghai University, Shanghai 200072, China
2.
School of Traffic and Transportation Engineering, Tongji University, Shanghai 200092, China

More Information

Author Bio:
Peng Miao-juan(1965-), female, EngD, associate professor, +86—21—56999934, mjpeng@staff.shu.edu.cn

摘要

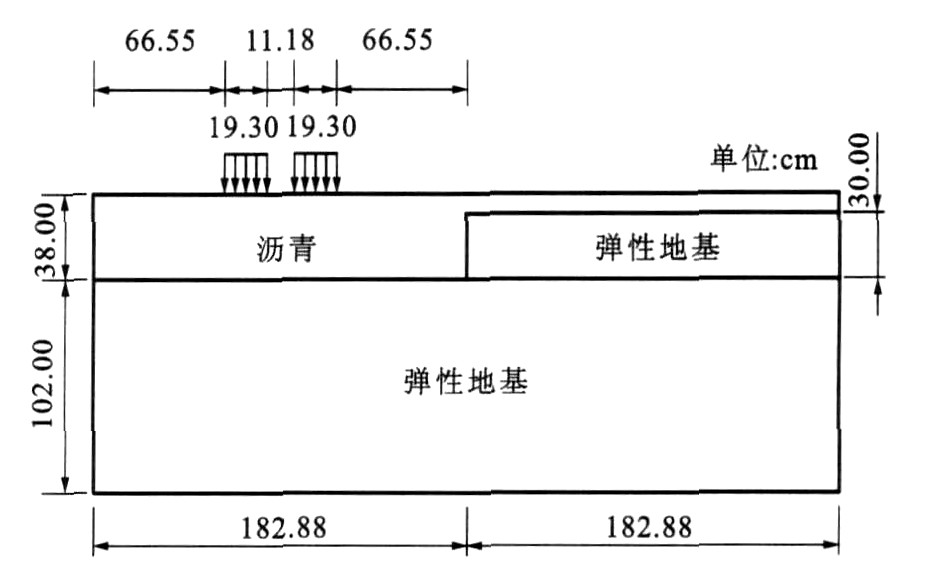
摘要: 为了正确预估沥青路面的永久变形, 对沥青路面永久变形的非线性粘弹性有限元法进行了研究, 推导了广义Maxwell模型的非线性粘弹性有限元法, 建立了沥青路面永久变形的非线性粘弹-弹塑性本构模型, 从弹性、非线性弹性、塑性、粘弹性、非线性粘弹性等方面对沥青路面的永久变形进行了分析, 对沥青路面的永久变形进行了计算, 并将计算结果和SHRP的计算结果以及SWK/UN轮辙试验结果进行了对比。计算结果表明: 沥青路面永久变形的非线性粘弹-弹塑性本构模型是有效的, 其路面变形计算值与SHRP的计算值相对误差为6.567%, 与SWK/UN轮辙试验值相对误差为6.069%。
- 路面工程 /
- 沥青路面 /
- 永久变形 /
- 广义Maxwell模型 /
- 粘弹性 /
- 非线性粘弹性有限元法
Abstract: In order to correctly predict the permanent deformation of asphalt pavement, nonlinear viscoelastic finite element method was studied, the finite element method of nonlinear viscoelasticity for generalized Maxwell model was deduced, a nonlinear viscoelastic-elastoplastic constitutive model of permanent deformation for asphalt pavementhen was set up, and the permanent deformation of asphalt pavement was analyzed depending on its material properties, such as elasticity, nonlinear elasticity, plasticity, viscoelasticity and nonlinear viscoelasticity, etc., the permanent deformation of asphalt pavement was simulated by using the model, SHRP and SWK/UN experiment, and the numerical results were compared.Comparison result shows that their relative error are 6.567% and 6.069% respectively, the model is effective.
- pavement engineering /
- asphalt pavement /
- permanent deformation /
- generalized Maxwell model /
- viscoelasticity /
- nonlinear viscoelastic finite element method

HTML全文

图 1 路面体系

Figure 1. Pavement system

下载: 全尺寸图片幻灯片

图 2 路面结构的有限元网格

Figure 2. Finite element mesh of pavement structure

下载: 全尺寸图片幻灯片

图 3 p₁路面的垂直变形

Figure 3. Vertical deformations of p₁pavement

下载: 全尺寸图片幻灯片

图 4 p₂路面的垂直变形

Figure 4. Vertical deformations of p₂pavement

下载: 全尺寸图片幻灯片

图 5 p₃路面的垂直变形

Figure 5. Vertical deformations of p₃pavement

下载: 全尺寸图片幻灯片

图 6 p₄路面的垂直变形

Figure 6. Vertical deformations of p₄pavement

下载: 全尺寸图片幻灯片

图 7 p₅路面的垂直变形

Figure 7. Vertical deformations of p₅pavement

下载: 全尺寸图片幻灯片

图 8 p₆路面的垂直变形

Figure 8. Vertical deformations of p₆pavement

下载: 全尺寸图片幻灯片

图 9 p₇路面的垂直变形

Figure 9. Vertical deformations of p₇pavement

下载: 全尺寸图片幻灯片

图 10 p₁路面变形对比

Figure 10. Deformation Comparison of p₁pavement

下载: 全尺寸图片幻灯片

表 1 沥青粘结料特性

Table 1. Asphalt binder properties

材料特性		基准材料
材料特性		AAC-1	AAG-1	AAK-1	AAM-1
粘度/针入度		AC-8	AR-4000	AC-30	AC-20
SHRP PG分级		PG58-16	PG58-10	PG64-22	PG64-16
原始沥青	动力粘度(60 ℃) / (Pa·s)	41.9	186.2	325.6	199.2
原始沥青	运动粘度(135 ℃) / (m²·s^-1)	1.79×10^-4	2.43×10^-4	5.62×10^-4	5.69×10^-4
老化沥青	动力粘度(60 ℃) / (Pa·s)	101.4	325.3	970.8	394.7
老化沥青	运动粘度(135 ℃) / (m²·s^-1)	2.39×10^-4	3.04×10^-4	9.30×10^-4	7.44×10^-4

下载: 导出CSV

表 2 混合料组成

Table 2. Mixture composition

路面类型	沥青粘结料	骨料	空隙率/%
p₁	AAK-1	RD	3.7
p₂	AAK-1	RD	6.5
p₃	AAC-1	RD	3.8
p₄	AAC-1	RD	6.5
p₅	AAM-1	RD	4.6
p₆	AAM-1	RD	7.5
p₇	AAG-1	RH	4.7

下载: 导出CSV

表 3 非线性弹性常数

Table 3. Nonlinear elasticity constants MPa

材料常数	路面类型
材料常数	p₁	p₂	p₃	p₄	p₅	p₆	p₇
C₁	5.06×10²	5.06×10²	4.36×10³	1.28×10³	2.68×10³	2.76×10³	5.78×10¹
C₂	-2.53×10²	-5.06×10²	-1.64×10²	-3.22×10²	-5.61×10³	-3.28×10³	-8.09×10²
C₃	-5.06×10⁴	-5.06×10⁴	-2.73×10⁶	-2.96×10⁴	-2.81×10⁶	-2.29×10⁶	-1.16×10⁶
C₄	5.06×10⁴	2.02×10⁵	1.09×10⁵	2.96×10⁵	1.12×10⁶	8.19×10⁵	1.16×10⁵
C₅	0.00	0.00	0.00	0.00	0.00	0.00	0.00
C₆	1.26×10⁸	2.53×10⁸	5.46×10⁶	4.74×10⁸	2.81×10⁸	4.14×10⁷	2.89×10⁸
C₇	-5.06×10⁷	-3.79×10⁷	-7.64×10⁷	-2.37×10⁷	-2.81×10⁷	-3.28×10⁶	-1.16×10⁷
C₈	5.06×10⁷	5.06×10⁷	1.09×10⁷	5.92×10⁷	2.81×10⁷	3.28×10⁵	1.16×10⁷
C₉	5.06×10⁵	5.06×10⁵	1.09×10⁶	8.88×10⁶	2.81×10⁷	6.55×10⁷	1.16×10⁶

下载: 导出CSV

表 4 粘弹性材料常数

Table 4. Viscoelastic material constants MPa

元件i

路面类型

p₁

p₂

p₃

p₄

E_i

η_i

E_i

η_i

E_i

η_i

E_i

η_i

3.67×10^-4

8.25×10^-1

3.67×10^-4

8.25×10^-1

3.89×10^-4

8.64×10^-1

1.81×10^-3

8.69×10^-1

6.24×10^-4

1.42×10^-1

6.34×10^-4

1.42×10^-1

6.28×10^-4

1.17×10^-1

2.37×10^-3

1.13×10^-1

1.10×10^-3

2.47×10^-2

1.10×10^-3

2.47×10^-2

7.20×10^-4

1.60×10^-2

3.11×10^-3

1.49×10^-2

2.61×10^-3

5.86×10^-3

2.61×10^-3

5.86×10^-3

9.70×10^-4

2.15×10^-3

4.02×10^-3

1.93×10^-3

4.23×10^-3

9.51×10^-4

4.23×10^-3

9.51×10^-4

1.40×10^-3

3.10×10^-4

4.98×10^-3

2.39×10^-4

1.92×10²

4.31×10^-4

1.92×10^-2

4.31×10^-4

5.53×10^-3

1.23×10^-4

4.16×10^-2

1.99×10^-4

1.71×10^-1

3.86×10^-4

1.72×10³

3.86×10^-4

8.92×10^-2

1.98×10^-4

9.36×10³

4.49×10^-4

8.00×10^-1

1.80×10^-4

8.00×10^-1

1.80×10^-4

9.00×10^-1

2.00×10^-4

0.00

元件i

路面类型

p₅

p₆

p₇

E_i

η_i

E_i

η_i

E_i

η_i

1.02×10^-2

8.63×10^-1

1.15×10^-2

8.65×10^-1

3.67×10^-4

8.68×10^-1

1.40×10^-2

1.18×10^-1

1.55×10^-2

1.17×10^-1

4.83×10^-4

1.14×10^-1

1.92×10^-2

1.62×10^-2

2.10×10^-2

1.58×10^-2

6.39×10^-4

1.51×10^-2

2.59×10^-2

2.19×10^-3

2.81×10^-2

2.12×10^-3

8.05×10^-4

1.91×10^-3

4.93×10^-2

4.16×10^-4

3.42×10^-2

2.58×10^-4

9.96×10^-4

2.36×10^-4

1.22×10^-1

1.03×10^-4

1.07×10^-1

8.09×10^-5

8.33×10^-3

1.97×10^-4

7.32×10^-1

6.17×10^-5

7.50×10^-1

5.66×10^-5

1.87×10^-1

4.44×10^-4

0.00

8.00×10^-1

1.89×10^-4

下载: 导出CSV

表 5 塑性材料常数

Table 5. Plastic material constants

材料常数	路面类型
材料常数	p₁	p₂	p₃	p₄	p₅	p₆	p₇
屈服应力/MPa	1.00	1.00	2.00	1.00×10^-3	3.00	3.00	1.00
强化系数	1.00×10³	1.00×10³	5.00×10²	5.00×10²	2.00×10³	2.00×10³	5.00×10²

下载: 导出CSV

表 6 沥青路面的车辙深度

Table 6. Rutting depth of asphalt pavement mm

下载: 导出CSV

参考文献(16)

[1]	Wu Zhong. Finite element simulation of rutting on superpave pavements[D]. Manhattan: Kansas State University, 2001.
[2]	Hua Jian-feng, White T. A study of nonlinear tire contact pressure effects on HMA rutting[J]. The International Journal of Geomechanics, 2002, 2 (3): 353-376. doi: 10.1061/(ASCE)1532-3641(2002)2:3(353)
[3]	Sousa J B, Weissman S L, Deacon J A, et al. Permanent deformation response of asphalt aggregate mixes[R]. Washington DC: National Research Program Council, 1994.
[4]	Long F M. Permanent deformation of asphalt concrete pavements: a nonlinear viscoelastic approach to mix analyses anddesign[D]. Berkeley: University of California at Berkeley, 2001.
[5]	Erkens S M J G, Liu X, Scarpas A. 3D finite model for asphalt concrete response simulation[J]. The International Journal of Geomechanics, 2002, 2 (3): 305-330. doi: 10.1061/(ASCE)1532-3641(2002)2:3(305)
[6]	Blab R, Harvey J T. Modeling measured 3D tire contact stress in a viscoelastoc FE pavement model[J]. The International Journal of Geomechanics, 2002, 2 (3): 271-290. doi: 10.1061/(ASCE)1532-3641(2002)2:3(271)
[7]	Judycki J. Non-linear viscoelastic behaviour of conventional and modified asphaltic concrete under creep[J]. Materialsand Structures, 1992, 25 (2): 95-101. doi: 10.1007/BF02472462
[8]	张宜洛, 郑南翔. 沥青混合料的基本参数对其高低温性能的影响[J]. 长安大学学报: 自然科学版, 2006, 26 (4): 35-39. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604008.htm Zhang Yi-luo, Zheng Nan-xiang. Influence of basic parameters on high and low temperature performances of bituminous mixture[J]. Journal of Chang'an University: Natural Science Edition, 2006, 26 (4): 35-39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200604008.htm
[9]	University of California at Berkeley, Oregon State University, Austin Research Engineers, et al. Validation of the relationship between asphalt properties and asphalt-aggregate mixperformance[R]. Washington DC: National Research Coun-cil, 1994.
[10]	杜顺成, 戴经梁. 沥青混合料永久变形评价指标[J]. 中国公路学报, 2006, 19 (5): 18-22. doi: 10.3321/j.issn:1001-7372.2006.05.004 Du Shun-cheng, Dai Jing-liang. Permanent deformation evaluation index of asphalt mixture[J]. China Journal of Highway and Transport, 2006, 19 (5): 18-22. (in Chinese) doi: 10.3321/j.issn:1001-7372.2006.05.004
[11]	刘红瑛, 戴经梁. 不同级配对沥青混合料车辙性能的影响[J]. 长安大学学报: 自然科学版, 2004, 24 (5): 11-15. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200405003.htm Liu Hong-ying, Dai Jing-liang. Effect of different gradations on asphalt mixture resistance to rut[J]. Journal of Chang'an University: Natural Science Edition, 2004, 24 (5): 11-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200405003.htm
[12]	韩海峰, 吕伟民, 何桂平. 水作用下沥青混合料永久变形特性的表现形式[J]. 中国公路学报, 2003, 16 (4): 4-8. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200304002.htm Han Hai-feng, Lu Wei-min, He Gui-ping. Effects of water on permanent deformation potential of hot-mix asphalt[J]. China Journal of Highway and Transport, 2003, 16 (4): 4-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200304002.htm
[13]	赵可, 卢永贵, 魏如喜. SMA高温稳定性研究[J]. 中国公路学报, 2004, 17 (2): 11-17. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200402003.htm Zhao Ke, Lu Yong-gui, Wei Ru-xi. Research on high temperature properties of SMA[J]. China Journal of Highwayand Transport, 2004, 17 (2): 11-17. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200402003.htm
[14]	武建民, 李晓军. 沥青混合料小梁疲劳试验的有限元模拟[J]. 长安大学学报: 自然科学版, 2004, 24 (1): 5-8. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200401002.htm Wu Jian-min, Li Xiao-jun. Simulation of asphalt mixtures beam test with finite-element method[J]. Journal of Chang'an University: Natural Science Edition, 2004, 24 (1): 5-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200401002.htm
[15]	张宜洛. 抗滑级配类型沥青混合料的抗滑性能[J]. 长安大学学报: 自然科学版, 2003, 23 (1): 7-10. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200301001.htm Zhang Yi-luo. Skid resistance regulatity of different grades bituminous mixture[J]. Journal of Chang'an University: Natural Science Edition, 2003, 23 (1): 7-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200301001.htm
[16]	Peng Miao-juan, Xu Zhi-hong. Research on nonlinear constitutive relationship of permanent deformation in asphalt pavements[J]. Science in China Series G: Physics, Mechanics & Astronomy, 2006, 49 (6): 671-682.

施引文献

资源附件(0)

访问统计

点击查看大图

图(10) / 表(6)

计量

文章访问数: 209
HTML全文浏览量: 93
PDF下载量: 692
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

沥青路面永久变形的非线性粘弹-弹塑性本构模型

作者简介:
彭妙娟(1965-)，女，山西稷山人.上海大学副教授，工学博士，从事道路工程研究

计量

Nonlinear viscoelastic-elastoplastic constitutive model of permanent deformation for asphalt pavement

Author Bio:
Peng Miao-juan(1965-), female, EngD, associate professor, +86—21—56999934, mjpeng@staff.shu.edu.cn

计量

目录

留言板

沥青路面永久变形的非线性粘弹-弹塑性本构模型

作者简介: 彭妙娟(1965-)，女，山西稷山人.上海大学副教授，工学博士，从事道路工程研究

计量

出版历程

Nonlinear viscoelastic-elastoplastic constitutive model of permanent deformation for asphalt pavement

Author Bio: Peng Miao-juan(1965-), female, EngD, associate professor, +86—21—56999934, mjpeng@staff.shu.edu.cn

计量

出版历程

目录

作者简介:
彭妙娟(1965-)，女，山西稷山人.上海大学副教授，工学博士，从事道路工程研究

Author Bio:
Peng Miao-juan(1965-), female, EngD, associate professor, +86—21—56999934, mjpeng@staff.shu.edu.cn