预应力混凝土梁非线性分析单元模型

张峰; 叶见曙; 徐向锋

预应力混凝土梁非线性分析单元模型

1.
东南大学交通学院，江苏南京 210096
2.
山东交通学院土木工程系，山东济南 250023

基金项目:

江苏省交通科学研究计划项目 04Y051

详细信息

作者简介:
张峰(1978-).男，江苏豢兴人，东南大学工学博士研究生.从事桥粱结构非线性研究

叶见曙(1948-), 男, 湖北武汉人, 东南大学教授

中图分类号: U441.5
计量
- 文章访问数: 328
- HTML全文浏览量: 134
- PDF下载量: 283
- 被引次数: 0
出版历程
- 收稿日期: 2007-02-16
- 刊出日期: 2007-10-25

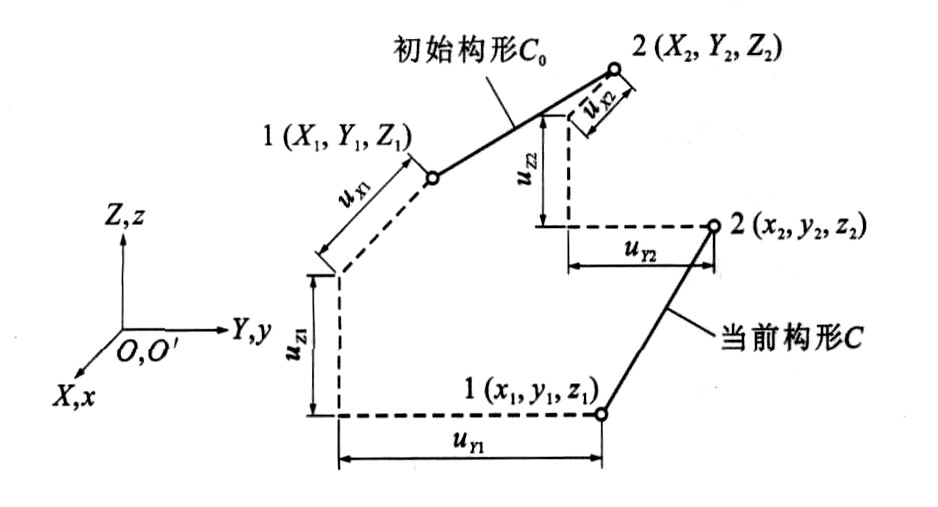
Nonlinear analysis element model of prestressed concrete beam

1.
School of Transportation, Southeast University, Nanjing 210096, Jiangsu, China
2.
Department of Civil Engineering, Shandong Jiaotong University, Jinan 250023, Shandong, China

More Information

Author Bio:
zhang Feng(1978-), male, doctoral student of engineering, +86-25-83794206, xxf19780311@163.com

Ye Jian-shu(1948-), male, professor, +86-25-86315379, yejianshu@seu.edu.cn

摘要

摘要: 为了能够准确有效地分析混凝土梁中预应力钢筋的力学性能, 模拟结构中存在的普通钢筋、预应力直线钢筋和预应力曲线钢筋, 提出了一种预应力混凝土梁非线性分析的单元模型。应用有限元理论, 采用全拉格朗日列式的三维杆单元模拟预应力钢筋; 采用实体退化组合壳单元模拟结构; 应用钢筋单元和混凝土单元之间的位移场关系形成钢筋对混凝土单元的贡献, 将预应力钢筋对结构的作用直接反映在单元模型内部。预应力混凝土T梁的破坏过程模拟结果表明梁的跨中挠度计算结果和试验实测数据吻合, 单元模型有效地反映了预应力束的力学性能。
- 桥梁工程 /
- 预应力混凝土梁 /
- 曲线预应力钢筋 /
- 实体退化组合壳单元 /
- 非线性分析 /
- 有限元程序
Abstract: In order to analyze the mechanics properties of tendon exactly and effectively, simulate normal steel bar, linear tendon and curved tendon in prestressed concrete beam, a nonlinear analysis element model of prestressed concrete beam was presented.In the model, based on finite element method, tendon was simulated by 3-D link bar element of total Lagrangian method, solid degenerated-combined shell element was used to simulate prestressed concrete beam, and the stiffness of link element contributing to concrete element was computed according to the displacement relationship of tendon element and shell element, the action of tendon contributing to the structure was directly reflected inside the element.The simulation result of the destroyed process of prestressed concrete T beam shows that the computation deflection and test deflection in middle span are accordant, and the model can simulate the mechanics properties of tendon.
- bridge engineering /
- prestressed concrete beam /
- curve prestressed bar /
- solid degenerated-combined shell element /
- nonlinear analysis /
- finite element program

HTML全文

图 1 两节点的杆单元

Figure 1. Two-node link element

下载: 全尺寸图片幻灯片

图 2 组合单元

Figure 2. Combined element

下载: 全尺寸图片幻灯片

图 3 混凝土本构关系

Figure 3. Constitutive equation of concrete

下载: 全尺寸图片幻灯片

图 4 试验梁及加载

Figure 4. Test beam and load

下载: 全尺寸图片幻灯片

图 5 有限元模型

Figure 5. Finite element model

下载: 全尺寸图片幻灯片

图 6 失效单元

Figure 6. Disabled element

下载: 全尺寸图片幻灯片

图 7 荷载与挠度曲线

Figure 7. Curves of load and deflection

下载: 全尺寸图片幻灯片

图 8 预应力束应力

Figure 8. Stress of prestressed bar

下载: 全尺寸图片幻灯片

表 1 混凝土力学性能

Table 1. Mechanical properties of concrete

梁编号	弹性模量/GPa	抗压强度/MPa	抗拉强度/MPa
1	35.40	36.0	3.30
2	36.70	36.2	3.40
平均值	36.05	36.1	3.35

下载: 导出CSV

表 2 预应力钢筋力学性能

Table 2. Mechanical properties of prestressed bar

试件编号	弹性模量/GPa	抗拉强度/MPa
1	224.0	1 680.0
2	218.0	1 680.0
3	214.0	1 605.0
4	219.0	1 605.0
5	221.0	1 680.0
6	221.0	1 640.0
平均值	219.5	1 648.3

下载: 导出CSV

参考文献(12)

[1]	刘龄嘉, 贺拴海, 陈偕民. 悬臂梁抗裂非线性分析[J]. 长安大学学报: 自然科学版, 2005, 25 (2): 65-68. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL20050200E.htm Liu Ling-jia, He Shuan-hai, Chen Xie-min. Nonlinear analysis for cantilever beam's anti-cracking[J]. Journal of Chang'an University: Natural Science Edition, 2005, 25 (2): 65-68. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL20050200E.htm
[2]	徐文平, 裴铭海, 戴捷, 等. 大跨简支系杆拱桥非线性稳定性[J]. 交通运输工程学报, 2005, 5 (4): 53-57. doi: 10.3321/j.issn:1671-1637.2005.04.011 Xu Wen-ping, Pei Ming-hai, Dai Jie, et al. Nonlinear stability of simply supported tied-arch bridge with long span[J]. Journal of Traffic and Transportation Engineering, 2005, 5 (4): 53-57. (in Chinese) doi: 10.3321/j.issn:1671-1637.2005.04.011
[3]	刘小燕, 颜东煌, 张峰, 等. 预应力高强混凝土梁极限承载力分析[J]. 中国公路学报, 2006, 19 (1): 58-61. doi: 10.3321/j.issn:1001-7372.2006.01.012 Liu Xiao-yan, Yan Dong-huang, Zhang Feng, et al. Ultimateload analysis of prestressed high-strength concrete beam[J]. China Journal of Highway and Transport, 2006, 19 (1): 58-61. (in Chinese) doi: 10.3321/j.issn:1001-7372.2006.01.012
[4]	Fragiacomo M, Amadio C, Asece M, et al. Finite-element model for collapse and long-term analysis of steel-concrete composite beams[J]. Journal of Structural Engineering, 2004, 130 (3): 489-497. doi: 10.1061/(ASCE)0733-9445(2004)130:3(489)
[5]	张峰, 叶见曙. 预应力混凝土梁开裂后的结构行为[J]. 东南大学学报: 自然科学版, 2005, 35 (4): 584-588. doi: 10.3321/j.issn:1001-0505.2005.04.019 Zhang Feng, Ye Jian-shu. Structure behavior of cracked prestressed concrete beam[J]. Journal of Southeast University: Natural Science Edition, 2005, 35 (4): 584-588. (in Chinese) doi: 10.3321/j.issn:1001-0505.2005.04.019
[6]	Deng Lin-zhong, Michel G, Ales Z, et al. Nonlinear flexural behavior of prestressed concrete girder bridges[J]. Journal ofBridge Engineering, 2001, 6 (4): 276-284. doi: 10.1061/(ASCE)1084-0702(2001)6:4(276)
[7]	Song H W, You D W, Byun KJ, et al. Finite element failureanalysis of reinforced concrete T girder[J]. Engineering Structures, 2002, 24 (3): 151-162.
[8]	张峰, 叶见曙. 预应力混凝土梁开裂后的受力性能分析[J]. 公路交通科技, 2005, 22 (7): 64-67. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200507016.htm Zhang Feng, Ye Jian-shu. Mechanical behavior of prestressed concrete beams after cracking[J]. Journal of Highway and Transportation Research and Development, 2005, 22 (7): 64-67. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200507016.htm
[9]	Wendel MS, Richard E M. Nonlinear FE analysis of steelconcrete composite structures[J]. Journal of Structural Engineering, 2000, 126 (6): 662-674. doi: 10.1061/(ASCE)0733-9445(2000)126:6(662)
[10]	Wonseok C, Elisa D S. Nonlinear finite-element analysis of composite steel girder bridges[J]. Journal of Structural Engineering, 2005, 131 (2): 304-313.
[11]	Wu Xiao-han. Tendon model for nonlinear analysis of prestressed concrete structures[J]. Journal of Structural Engineering, 2001, 127 (4): 398-405.
[12]	Kitjapat P. Nonlinear finite element for reinforced concreteslabs[J]. Journal of Structural Engineering, 2005, 131 (4): 643-649.