0.   引言

列车脱轨将会给人民的生命和财产安全带来重大损失, 因而安全运行的最基本要求是保证列车不发生脱轨事故。随着运行速度的不断提高, 列车运行的安全问题更加突出, 高速重载运行的列车一旦脱轨将会带来更大的灾难。虽然自从1908年法国学者Nadal提出了著名的脱轨系数判别准则以来, 已经有近百年的历史, 广大铁路科研工作者对脱轨问题也进行了长期大量的研究, 但这个问题目前仍然没有得到很好解决, 脱轨事故还是时有发生, 因此, 从机理上掌握轮对的脱轨规律, 提出更加合理的脱轨判别准则是非常必要的。

轮对爬轨脱轨是脱轨的一种重要形式, 主要发生于曲线轨道上, 通常由于大的轮轨横向力或大的轮重减载引起, 其爬轨过程可以认为是准静态的, 即忽略轮对的惯性效应。爬轨脱轨的判别有至今还在广泛采用的著名的Nadal公式, 但其是基于简单的轮轨力平衡关系得出的, 脱轨的判别偏于保守^[1], 有很大的局限性; Karmel和Sweet采用详细的脱轨模型和轮对比例模型实验装置进行研究, 给出了车轮准静态爬轨脱轨准则^[2-3]; Weinstock对Nadal准则进行了改进, 综合考虑了轮缘贴靠侧和非轮缘贴靠侧的脱轨系数^[4]; Elkins和Wu提出了基于车轮横向力与垂向力比值的距离历程的脱轨准则, 考虑了轮对摇头角的影响^[5]; 文献[6]采用全比例滚动台进行了单轮对准静态脱轨过程及不同参数影响的试验研究; 文献[7]建立了轮对三维模型, 推导出爬轨的脱轨系数公式, 并通过数值计算验证了与经典公式的一致性。在国内, 曾庆元等首次提出了用能量随机分析方法来判别列车脱轨^[8]; 俞展猷等详述了脱轨过程和脱轨过程中轮轨的几何接触状态, 考察了相关参数对脱轨系数限界值的影响, 给出了通用的脱轨安全性评价方法^[9]; 翟婉明等基于车辆-轨道耦合动力学理论对列车脱轨进行了研究, 提出直接根据车轮抬升量评判脱轨的原理与方法^[10]; 文献[11]在试验台上再现了脱轨现象, 并给出了轮重减载率对脱轨的影响规律; 文献[12]则通过建立非对称车辆/轨道耦合动力学模型, 研究了轨道扣件失效对车辆动态脱轨的影响。

虽然各国学者从理论和试验两方面致力于脱轨系数与轮重减载率的量值研究, 并制定了各自的规范限值, 有关脱轨研究成果对预防列车脱轨发挥了重要作用。但由于此问题的复杂性, 已有脱轨评价标准存在一定局限性, 因此, 非常有必要从脱轨机理和判别准则方面进行更深入研究, 找到脱轨的内在规律, 提出更加合理的轮对爬轨脱轨的判别准则。

1.   轮对受力分析

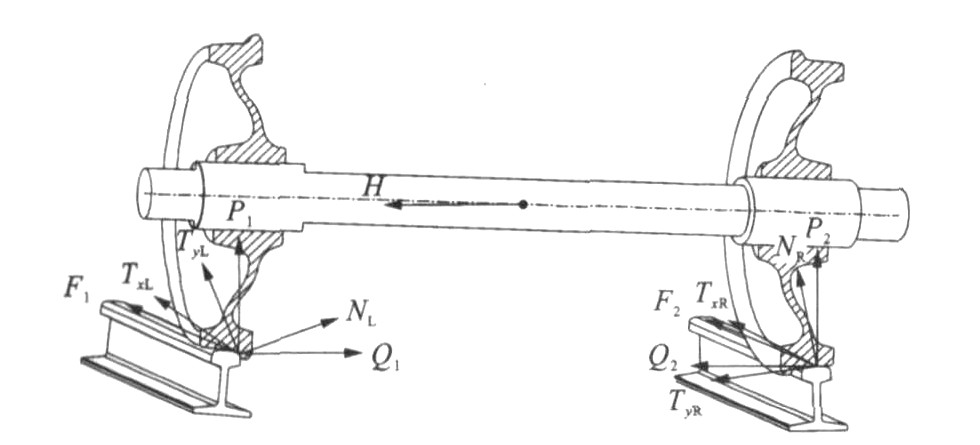
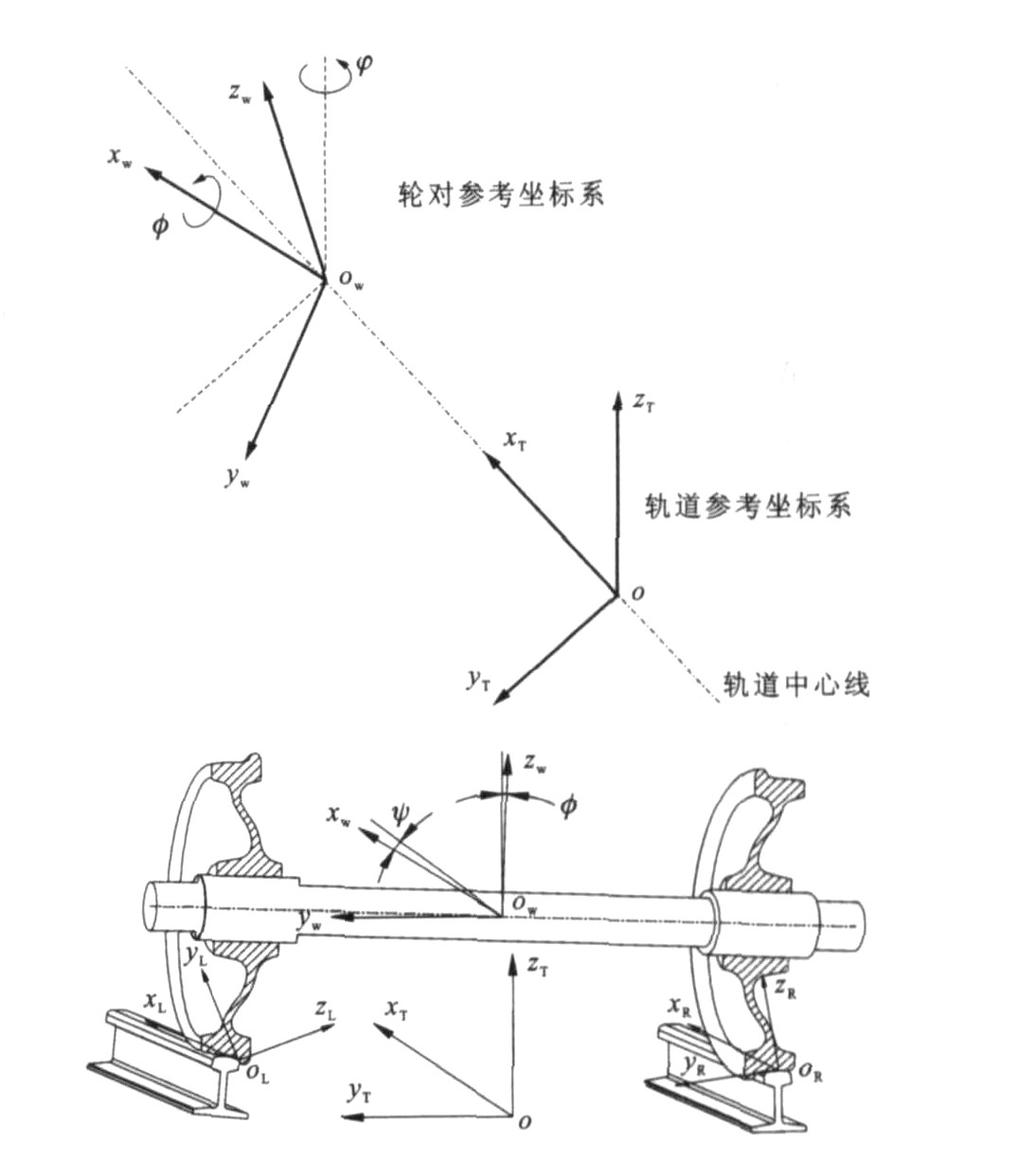
轮对是铁道车辆走行部的最关键部件, 其一方面要承受来自轨道的作用力, 另一方面要承受来自上部车辆的重力和振动, 轮对的受力状态以及和钢轨的作用关系决定着车辆的运行安全, 车辆的脱轨归根结底是轮轨间的相互作用关系发生了变化, 满足不了车轮在轮轨正常接触范围内运行, 因此, 对于脱轨机理的研究应从轮对的受力状态和轮轨相互作用关系的角度来进行。本文假设轮对是刚性的且不跳离钢轨, 轨道和轮对的笛卡儿坐标系见图 1。轨道坐标系ox_Ty_Tz_T的原点位于轨道中心线并以速度v相对于固定的惯性参考系运动。o_wx_wy_wz_w为固结于轮对质心坐标系, 与轮对一起运动。此外, 还有与轮对一起运动的左右轮轨接触点坐标系o_Lx_Ly_Lz_L和o_Rx_Ry_Rz_R。

图  1  轨道和轮对坐标系

Figure  1.  Coordinate systems of track and wheelset

下载: 全尺寸图片 幻灯片

各坐标系之间有如下变换关系

$\begin{array}{l}\left[\begin{array}{c}i{}_{\text{Τ}}\\ j{}_{\text{Τ}}\\ k{}_{\text{Τ}}\end{array}\right]=\left[\begin{array}{ccc}\cos (\psi )& -\cos (\text{ϕ})\sin (\psi )& \sin (\text{ϕ})\sin (\psi )\\ \sin (\psi )& \cos (\text{ϕ})\cos (\psi )& -\sin (\text{ϕ})\cos (\psi )\\ 0& \sin (\text{ϕ})& \cos (\text{ϕ})\end{array}\right]\left[\begin{array}{c}i{}_{\text{w}}\\ j{}_{\text{w}}\\ k{}_{\text{w}}\end{array}\right](1)\\ \left[\begin{array}{c}i{}_{\text{w}}\\ j{}_{\text{w}}\\ k{}_{\text{w}}\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos (\delta {}_{\text{L}})& -\sin (\delta {}_{\text{L}})\\ 0& \sin (\delta {}_{\text{L}})& \cos (\delta {}_{\text{L}})\end{array}\right]\left[\begin{array}{c}i{}_{\text{L}}\\ j{}_{\text{L}}\\ k{}_{\text{L}}\end{array}\right](2)\\ \left[\begin{array}{c}i{}_{\text{w}}\\ j{}_{\text{w}}\\ k{}_{\text{w}}\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos (\delta {}_{\text{R}})& \sin (\delta {}_{\text{R}})\\ 0& -\sin (\delta {}_{\text{R}})& \cos (\delta {}_{\text{R}})\end{array}\right]\left[\begin{array}{c}i{}_{\text{R}}\\ j{}_{\text{R}}\\ k{}_{\text{R}}\end{array}\right](3)\end{array}$

式中: [i_Tj_Tk_T]^T、[i_wj_wk_w]^T、[i_Lj_Lk_L]^T和[i_Rj_Rk_R]^T分别为对应于轨道、轮对和左右轮轨接触点坐标系的单位矩阵; ψ和ϕ为轮对的摇头角和侧滚角; δ_L、δ_R分别为左右轮轨接触角。考虑到ψ和ϕ是小量, 于是式(1)变为

$\left[\begin{array}{c}i{}_{\text{Τ}}\\ j{}_{\text{Τ}}\\ k{}_{\text{Τ}}\end{array}\right]=\left[\begin{array}{ccc}1& -\psi & 0\\ \psi & 1& -\text{ϕ}\\ 0& \text{ϕ}& 1\end{array}\right]\left[\begin{array}{c}i{}_{\text{w}}\\ j{}_{\text{w}}\\ k{}_{\text{w}}\end{array}\right](4)$

最后, 可导出左右轮轨接触坐标系和轨道坐标系之间的变换方程为

$\begin{array}{l}\left[\begin{array}{c}i{}_{\text{Τ}}\\ j{}_{\text{Τ}}\\ k{}_{\text{Τ}}\end{array}\right]=\left[\begin{array}{ccc}1& -\psi \cos (\delta {}_{\text{L}})& \psi \sin (\delta {}_{\text{L}})\\ \psi & \cos (\delta {}_{\text{L}})-\text{ϕ}\sin (\delta {}_{\text{L}})& -\sin (\delta {}_{\text{L}})-\text{ϕ}\cos (\delta {}_{\text{L}})\\ 0& \sin (\delta {}_{\text{L}})+\text{ϕ}\cos (\delta {}_{\text{L}})& \cos (\delta {}_{\text{L}})-\text{ϕ}\sin (\delta {}_{\text{L}})\end{array}\right]\left[\begin{array}{c}i{}_{\text{L}}\\ j{}_{\text{L}}\\ k{}_{\text{L}}\end{array}\right](5)\\ \left[\begin{array}{c}i{}_{\text{Τ}}\\ j{}_{\text{Τ}}\\ k{}_{\text{Τ}}\end{array}\right]=\left[\begin{array}{ccc}1& -\psi \cos (\delta {}_{\text{R}})& -\psi \sin (\delta {}_{\text{R}})\\ \psi & \cos (\delta {}_{\text{R}})+\text{ϕ}\sin (\delta {}_{\text{R}})& \sin (\delta {}_{\text{R}})-\text{ϕ}\cos (\delta {}_{\text{R}})\\ 0& -\sin (\delta {}_{\text{R}})+\text{ϕ}\cos (\delta {}_{\text{R}})& \cos (\delta {}_{\text{R}})+\text{ϕ}\sin (\delta {}_{\text{R}})\end{array}\right]\left[\begin{array}{c}i{}_{\text{R}}\\ j{}_{\text{R}}\\ k{}_{\text{R}}\end{array}\right](6)\end{array}$

图  2  作用于轮对上的力

Figure  2.  Forces acted on wheelset

下载: 全尺寸图片 幻灯片

图 2中定义于轨道坐标系中的F₁₍₂₎、Q₁₍₂₎和P₁₍₂₎分别为作用于轮对上的左(右)轮轨接触点处的纵向、横向和垂向力, T_xL(R)、T_yL(R)和N_L(R)定义于轮轨接触坐标系, 为作用于轮对上的左(右)轮轨接触点处的纵向和横向的切向力及法向力, 那么, 两坐标系内的轮轨力间有如下变换关系

$\begin{array}{l}\left[\begin{array}{c}F{}_1\\ -Q{}_1\\ {\rm P}{}_1\end{array}\right]=\left[\begin{array}{ccc}1& -\psi \cos (\delta {}_{\text{L}})& \psi \sin (\delta {}_{\text{L}})\\ \psi & \cos (\delta {}_{\text{L}})-\text{ϕ}\sin (\delta {}_{\text{L}})& -\sin (\delta {}_{\text{L}})-\text{ϕ}\cos (\delta {}_{\text{L}})\\ 0& \sin (\delta {}_{\text{L}})+\text{ϕ}\cos (\delta {}_{\text{L}})& \cos (\delta {}_{\text{L}})-\text{ϕ}\sin (\delta {}_{\text{L}})\end{array}\right]\left[\begin{array}{c}{\rm T}{}_{x\text{L}}\\ {\rm T}{}_{y\text{L}}\\ {\rm N}{}_{\text{L}}\end{array}\right](7)\\ \left[\begin{array}{c}F{}_2\\ Q{}_2\\ {\rm P}{}_2\end{array}\right]=\left[\begin{array}{ccc}1& -\psi \cos (\delta {}_{\text{R}})& -\psi \sin (\delta {}_{\text{R}})\\ \psi & \cos (\delta {}_{\text{R}})+\text{ϕ}\sin (\delta {}_{\text{R}})& \sin (\delta {}_{\text{R}})-\text{ϕ}\cos (\delta {}_{\text{R}})\\ 0& -\sin (\delta {}_{\text{R}})+\text{ϕ}\cos (\delta {}_{\text{R}})& \cos (\delta {}_{\text{R}})+\text{ϕ}\sin (\delta {}_{\text{R}})\end{array}\right]\left[\begin{array}{c}{\rm T}{}_{x\text{R}}\\ {\rm T}{}_{y\text{R}}\\ {\rm N}{}_{\text{R}}\end{array}\right](8)\end{array}$

由于轮对侧滚角ϕ很小, 如忽略其影响, 则根据式(7)、(8)可导出轮轨横向力和垂向力的比值为

$\begin{array}{l}\frac{Q{}_1}{{\rm P}{}_1}=\frac{-{\rm T}{}_{x\text{L}}\psi -{\rm T}{}_{y\text{L}}\cos (\delta {}_{\text{L}})+{\rm N}{}_{\text{L}}\sin (\delta {}_{\text{L}})}{{\rm T}{}_{y\text{L}}\sin (\delta {}_{\text{L}})+{\rm N}{}_{\text{L}}\cos (\delta {}_{\text{L}})}(9)\\ \frac{Q{}_2}{{\rm P}{}_2}=\frac{{\rm T}{}_{x\text{R}}\psi +{\rm T}{}_{y\text{R}}\cos (\delta {}_{\text{R}})+{\rm N}{}_{\text{R}}\sin (\delta {}_{\text{R}})}{-{\rm T}{}_{y\text{R}}\sin (\delta {}_{\text{R}})+{\rm N}{}_{\text{R}}\cos (\delta {}_{\text{R}})}(10)\end{array}$

2.   轮轨二维接触脱轨准则

如只考虑轮轨二维接触问题, 取ψ为0, 则式(9)、(10)可写成

$\begin{array}{l}\frac{Q{}_1}{{\rm P}{}_1}=\frac{{\rm N}{}_{\text{L}}\tan (\delta {}_{\text{L}})-{\rm T}{}_{y\text{L}}}{{\rm N}{}_{\text{L}}+{\rm T}{}_{y\text{L}}\tan (\delta {}_{\text{L}})}(11)\\ \frac{Q{}_2}{{\rm P}{}_2}=\frac{{\rm N}{}_{\text{R}}\tan (\delta {}_{\text{R}})+{\rm T}{}_{y\text{R}}}{{\rm N}{}_{\text{R}}-{\rm T}{}_{y\text{R}}\tan (\delta {}_{\text{R}})}(12)\end{array}$

轮轨间为全滑动时, 左右轮轨横向与切向力为

$\begin{array}{l}{\rm T}{}_{y\text{L}}=\mu {}_{\text{L}}{\rm N}{}_{\text{L}}\\ {\rm T}{}_{y\text{R}}=\mu {}_{\text{R}}{\rm N}{}_{\text{R}}\end{array}$

式中: μ_L、μ_R为左右轮轨间的摩擦系数。于是式(11)、(12)变为

$\begin{array}{l}\frac{Q{}_1}{{\rm P}{}_1}=\frac{\tan (\delta {}_{\text{L}})-\mu {}_{\text{L}}}{1+\mu {}_{\text{L}}\tan (\delta {}_{\text{L}})}(13)\\ \frac{Q{}_2}{{\rm P}{}_2}=\frac{\tan (\delta {}_{\text{R}})+\mu {}_{\text{R}}}{1-\mu {}_{\text{R}}\tan (\delta {}_{\text{R}})}(14)\end{array}$

如果左侧车轮的δ_L达到最大接触角, 即轮缘接触角, 则车轮就到达爬轨的临界点, 有可能爬上钢轨顶面而发生脱轨。式(13)就是著名的Nadal公式, 比值Q₁/P₁称为车轮脱轨系数。

根据图 2可列出轮对横向力平衡方程为

${\rm H}=Q{}_1-Q{}_2(15)$

定义

$\{\begin{array}{l}{\rm P}{}_1=\left(1-\frac{\text{Δ}{\rm P}}{{\rm P}}\right){\rm P}\\ {\rm P}{}_2=\left(1+\frac{\text{Δ}{\rm P}}{{\rm P}}\right){\rm P}\end{array}(16)$

式中: P为左右车轮平均轮轨垂向力, 即车轮重力; ΔP为轮重减载量; ΔP/P为轮重减载率。根据式(13)~(16), 可导出轮对的临界脱轨条件为

$\begin{array}{l}\frac{{\rm H}}{{\rm P}}+\left[\frac{\tan (\delta {}_{\text{L}})-\mu {}_{\text{L}}}{1+\mu {}_{\text{L}}\tan (\delta {}_{\text{L}})}+\frac{\tan (\delta {}_{\text{R}})+\mu {}_{\text{R}}}{1-\mu {}_{\text{R}}\tan (\delta {}_{\text{R}})}\right]\frac{\text{Δ}{\rm P}}{{\rm P}}=\\ \frac{\tan (\delta {}_{\text{L}})-\mu {}_{\text{L}}}{1+\mu {}_{\text{L}}\tan (\delta {}_{\text{L}})}-\frac{\tan (\delta {}_{\text{R}})+\mu {}_{\text{R}}}{1-\mu {}_{\text{R}}\tan (\delta {}_{\text{R}})}(17)\end{array}$

在此定义H/P为轮轴脱轨系数, 式(17)称为轮对爬轨脱轨判别的二维准则。尽管本文采用与文献[13]不同的方法, 但导出的脱轨判别准则是一致的。

如果轮轴横向力H为0, 则从式(17)可得到

$\frac{\text{Δ}{\rm P}}{{\rm P}}=\frac{\left[\frac{\tan (\delta {}_{\text{L}})-\mu {}_{\text{L}}}{1+\mu {}_{\text{L}}\tan (\delta {}_{\text{L}})}-\frac{\tan (\delta {}_{\text{R}})+\mu {}_{\text{R}}}{1-\mu {}_{\text{R}}\tan (\delta {}_{\text{R}})}\right]}{\left[\frac{\tan (\delta {}_{\text{L}})-\mu {}_{\text{L}}}{1+\mu {}_{\text{L}}\tan (\delta {}_{\text{L}})}+\frac{\tan (\delta {}_{\text{R}})+\mu {}_{\text{R}}}{1-\mu {}_{\text{R}}\tan (\delta {}_{\text{R}})}\right]}(18)$

式(18)就是目前中国广泛采用轮重减载率进行脱轨判别的公式, 当轮重减载率超过左边项表示的临界值时, 车轮有可能爬上钢轨而发生脱轨。由于轮重减载率脱轨判别式是在假设轮轴横向力为零的前提下导出的, 而且要求脱轨侧车轮必须轮缘贴靠, 也就是说这时的车轮脱轨系数也同时处于临界值。很显然, 目前单独采用轮重减载率来进行脱轨的判别是不合理的, 除非同时知道这时的轮轴横向力为零, 且车轮处于轮缘贴靠状态。

因此, 采用式(17)比单独采用车轮脱轨系数式(13)或轮重减载率式(18)来进行脱轨的判别更为合理。式(17)的特点是联合采用轮轴脱轨系数和轮重减载率来判断脱轨, 其应用前提是轮轴横向力H≥0和左侧车轮必须贴靠轮缘, 这样车轮才有可能爬上钢轨而脱轨。但是, 该脱轨判别式考虑的是轮轨二维接触问题, 没有考虑轮对摇头角对脱轨的影响, 众所周知, 轮对摇头角对脱轨的影响是非常大的, 因此, 非常有必要对考虑轮轨三维接触关系的脱轨问题进行深入研究。

3.   轮轨三维接触脱轨准则

根据式(9)、(10)、(15)与(16), 可导出轮轨三维接触情况下的轮对临界脱轨条件为

$\begin{array}{l}\frac{{\rm H}}{{\rm P}}=\frac{-{\rm T}{}_{x\text{L}}\psi -{\rm T}{}_{y\text{L}}\cos (\delta {}_{\text{L}})+{\rm N}{}_{\text{L}}\sin (\delta {}_{\text{L}})}{{\rm T}{}_{y\text{L}}\sin (\delta {}_{\text{L}})+{\rm N}{}_{\text{L}}\cos (\delta {}_{\text{L}})}\left(1-\frac{\text{Δ}{\rm P}}{{\rm P}}\right)-\\ \frac{{\rm T}{}_{x\text{R}}\psi +{\rm T}{}_{y\text{R}}\cos (\delta {}_{\text{R}})+{\rm N}{}_{\text{R}}\sin (\delta {}_{\text{R}})}{-{\rm T}{}_{y\text{R}}\sin (\delta {}_{\text{R}})+{\rm N}{}_{\text{R}}\cos (\delta {}_{\text{R}})}\left(1+\frac{\text{Δ}{\rm P}}{{\rm P}}\right)(19)\end{array}$

轮轨纵向和横向切向力与轮轨切向速度或蠕滑率有关, 左右车轮的轮轨纵向和横向蠕滑率为

$\begin{array}{l}\{\begin{array}{l}\xi {}_{x\text{L}}=1-\frac{r{}_{\text{L}}}{r{}_0}\\ \xi {}_{y\text{L}}=-\psi \sec (\delta {}_{\text{L}})\end{array}(20)\\ \{\begin{array}{l}\xi {}_{x\text{R}}=1-\frac{r{}_{\text{R}}}{r{}_0}\\ \xi {}_{y\text{R}}=-\psi \sec (\delta {}_{\text{R}})\end{array}(21)\end{array}$

式中: r₀、r_L和r_R分别为车轮滚动圆半径、左轮和右轮的接触半径。与轮轨二维接触情况一样, 同样假设轮对处于脱轨临界状态时轮轨间发生完全滑动, 因此, 根据摩擦定律, 轮轨切向力和法向力关系为

$\{\begin{array}{l}{\rm T}{}_{xi}=-\frac{\xi {}_{xi}}{\sqrt{\xi {}_{xi}^2+\xi {}_{yi}^2}}\mu {}_i{\rm N}{}_i\\ {\rm T}{}_{y\text{i}}=-\frac{\xi {}_{yi}}{\sqrt{\xi {}_{xi}^2+\xi {}_{yi}^2}}\mu {}_i{\rm N}{}_i\\ i=\text{L},\text{R}\end{array}(22)$

将式(20)、(21)代入式(22), 然后将式(22)代入式(19), 最后得轮对临界脱轨条件为

$\begin{array}{l}\frac{{\rm H}}{{\rm P}}+(C{}_1+C{}_2)\frac{\text{Δ}{\rm P}}{{\rm P}}=C{}_1-C{}_2(23)\\ C{}_1=\frac{-\mu {}_{\text{L}}\psi r{}_{\text{L}}/r{}_0+\sin (\delta {}_{\text{L}})\sqrt{\left(1-r{}_{\text{L}}/r{}_0\right){}^2+\psi {}^2\sec {}^2(\delta {}_{\text{L}})}}{\mu {}_{\text{L}}\psi \tan (\delta {}_{\text{L}})+\cos (\delta {}_{\text{L}})\sqrt{\left(1-r{}_{\text{L}}/r{}_0\right){}^2+\psi {}^2\sec {}^2(\delta {}_{\text{L}})}}(24)\\ C{}_2=\frac{\mu {}_{\text{R}}\psi r{}_{\text{R}}/r{}_0+\sin (\delta {}_{\text{R}})\sqrt{\left(1-r{}_{\text{R}}/r{}_0\right){}^2+\psi {}^2\sec {}^2(\delta {}_{\text{R}})}}{-\mu {}_{\text{R}}\psi \tan (\delta {}_{\text{R}})+\cos (\delta {}_{\text{R}})\sqrt{\left(1-r{}_{\text{R}}/r{}_0\right){}^2+\psi {}^2\sec {}^2(\delta {}_{\text{R}})}}(25)\end{array}$

式(23)可称为轮对爬轨脱轨判别的三维准则, 实际应用时只需根据轮轨间横向力、垂向力和轮对摇头角进行脱轨的判断。

4.   实例分析

轮对的基本参数见表 1。本文认为轮缘贴靠的左侧轮轨摩擦系数大于踏面接触的右侧轮轨摩擦系数, 即取μ_L为1.2μ_R。当对表 1中某一参数对脱轨的影响进行变参数研究时, 其他参数不变化。

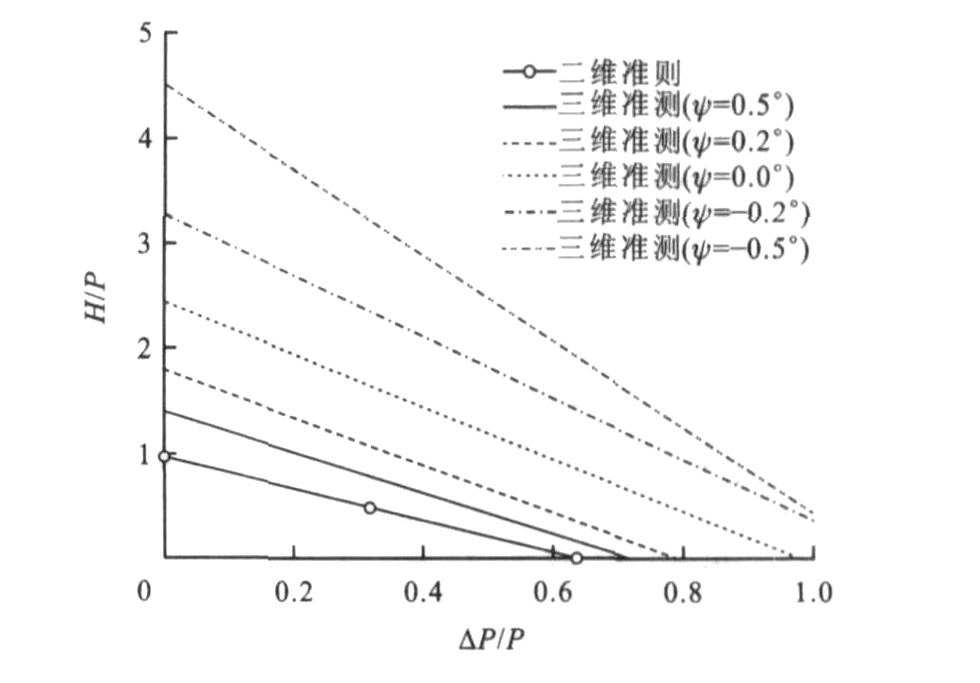
表  1  轮对基本参数

Table  1.  Wheelset basic parameters

μL	μR	δL/(°)	δR/(°)	rR/m	ψ/(°)	r0/m	rL/m
0.3	0.25	68	1.5	0.456 5	0.2	0.457 5	0.475

下载: 导出CSV 

| 显示表格

图  3  轮对爬轨脱轨临界曲线

Figure  3.  Critical curves of wheelset climb derailment

下载: 全尺寸图片 幻灯片

那么, 根据表 1的轮对基本参数值以及式(17)和(23), 就可计算出轮对爬轨脱轨判别的二维和三维准则的临界曲线, 见图 3。可知: 大的轮轴脱轨系数和轮重减载率都会增大脱轨的危险性; 二维脱轨判别准则与三维准则相比偏于保守; 负摇头角有利于防止脱轨, 正摇头角增大了脱轨的可能性; 正摇头角越大, 三维准则的临界脱轨曲线越接近于二维准则。

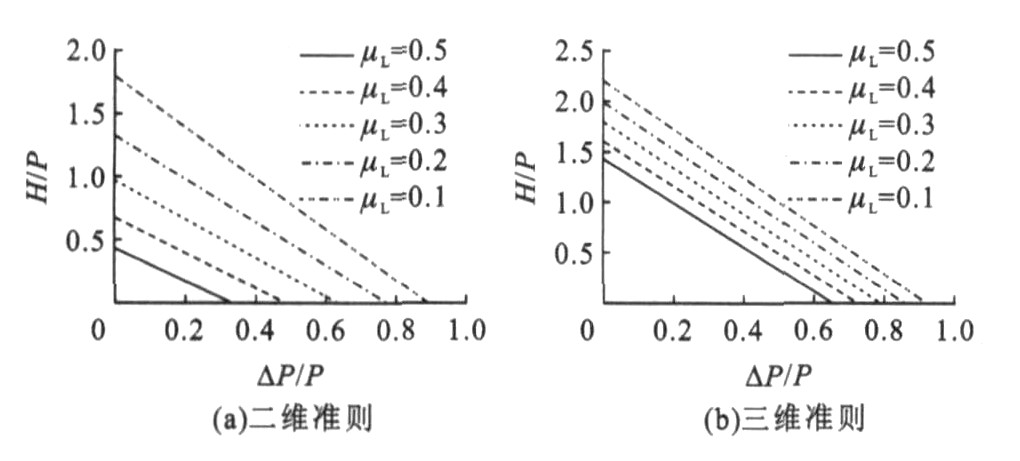
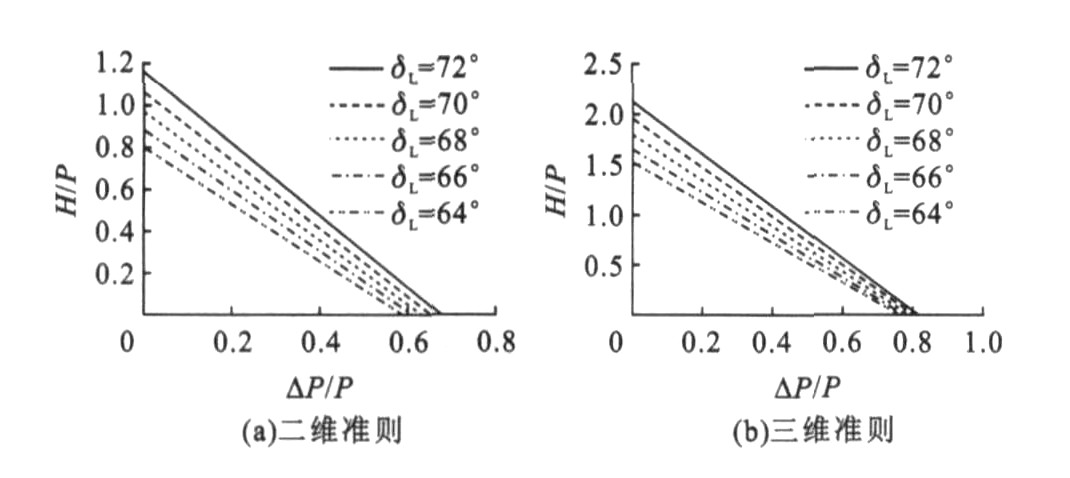
图 4为轮轨摩擦系数μ_L对脱轨的影响。可知: 无论是二维脱轨准则还是三维脱轨准则, μ_L越大, 越易脱轨, 而二维脱轨准则的摩擦系数对脱轨的影响要更显著。轮缘角δ_L对脱轨的影响见图 5, 加大δ_L有利于防止脱轨。

图  4  摩擦系数对脱轨的影响

Figure  4.  Effect of friction coefficient on derailment

下载: 全尺寸图片 幻灯片

图  5  轮缘角对脱轨的影响

Figure  5.  Effect of flange angle on derailment

下载: 全尺寸图片 幻灯片

5.   结语

通过进行轮对的三维空间受力分析, 推导出了轮轨横向力和垂向力比值的一般表示式, 并由此导出了轮对二维和三维脱轨判别准则的表达式, 联合采用轮轴脱轨系数和轮重减载率进行脱轨的判别。实例计算结果表明: 二维脱轨判别准则与三维准则相比偏于保守; 摇头角越小甚至变负越有利于防止脱轨, 摇头角越大, 三维准则的临界脱轨曲线越接近于二维准则; 减小轮轨摩擦系数与增大轮缘角有利于防止脱轨的发生。