0.   引言

目前沥青路面设计方法中, 主要把车辆载荷视为静载荷或近似等效静载荷, 没有考虑路面随机不平度对车辆振动的影响^[1-3], 这在车速较低, 车载较小时是比较合适的。但随着高速公路交通网致密化, 交通车辆组成必然向高速重载方向发展。由于车速的提高和载质量的增大, 使车辆在运动状态下由于振动所引起的惯性荷载和冲击荷载会大大增加, 这时仍旧使用静载模式已不能反映路面的实际受力状况, 无法解释动态载荷作用下路面结构产生的各种现象。基于此, 本文从随机路面谱出发, 模拟出路面随机不平度的时域模型, 并在路面随机不平度激励下进行了车辆对路面动载的数值仿真。

1.   路面随机不平度的时域模拟

路面不平度是指路表相对于基准平面的偏离。研究表明, 路面不平度是服从Gaussian概率分布的具有零均值的均匀随机场, 若转化为随机过程, 则具有平稳遍历特性。路面不平度的特性可用功率谱密度函数(PSD)S_R(ϕ)来表示^[3], 即

$S{}_{\text{R}}(\text{ϕ})=S{}_{\text{R}}(\text{ϕ}{}_0)\left(\frac{\text{ϕ}}{\text{ϕ}{}_0}\right){}^{-w}(1)$

式中: ϕ为空间频率/m^-1; ϕ₀为参考空间频率, 取0.1 m^-1; w为频率指数, 取2;S_R(ϕ₀)为参考空间频率下的路面功率谱密度值, 称为路面不平度系数。

根据GB7031-86的分级方法, 将路面按照功率谱分成八级, 从A级到H级路面等级依次降低^[4]。对于平稳Gaussian随机过程, 有多种方法可以生成路面不平度时域模型。基于幂函数的PSD, 可采用FFT逆变换法将路面功率谱生成随机道路不平度, 所模拟出的路面随机不平度q(t)为^[5]

$q(t)={\displaystyle \sum _{i=1}^n\sqrt{4S{}_{\text{R}}(\text{ϕ}{}_i)\text{Δ}\text{ϕ}}}\cos (\text{ϕ}{}_{i}vt-\theta {}_i)(2)$

式中: θ_i为[0, 2π]上均匀分布的随机数; v为车速; t为行驶时间; Δϕ为空间频率增量。

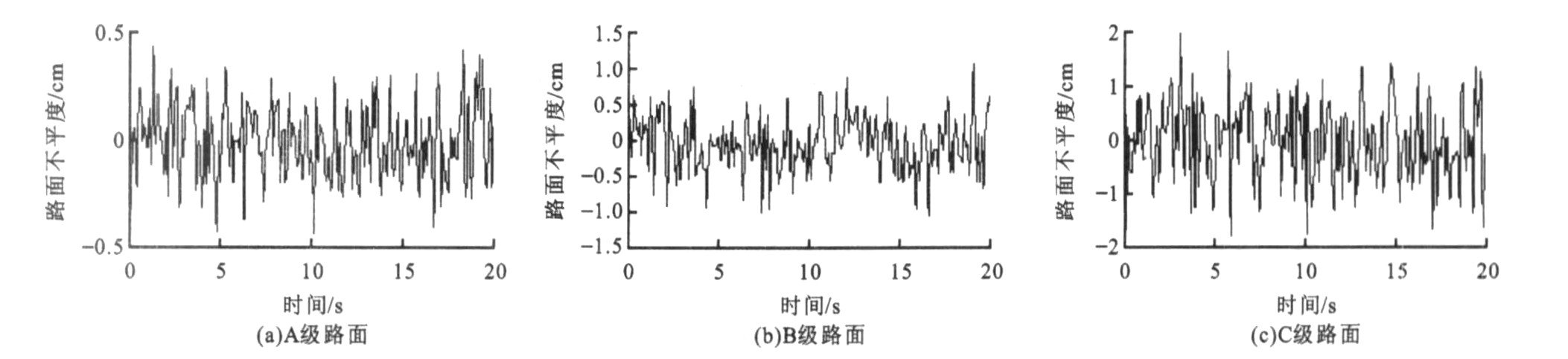
通过Matlab软件对汽车在速度为30 m·s^-1行驶时路面不平度的仿真, 可得到A~C级路面不平度随时间的变化, 见图 1。

图  1  路面随机不平度

Figure  1.  Road random roughness

下载: 全尺寸图片 幻灯片

2.   二分之一车辆模型

车辆是一个复杂的多自由度振动系统, 为了方便研究, 同时又尽可能与车辆实际情况相适应, 假设如下。

(1) 车身为刚体且左右对称, 前后桥为集中质量。

(2) 左右车轮受到的路面不平度激励相同, 前后轮受到的激励不相同。

(3) 车辆等速直线行使, 轮胎与地面始终保持接触, 无跳起。

(4) 车身只有垂直振动和俯仰振动, 对路面的振动荷载影响较大。

(5) 考虑到车辆和路面为弱耦合系统^{[3, 6]}, 仿真时可不考虑动弯沉量对车辆振动的影响。

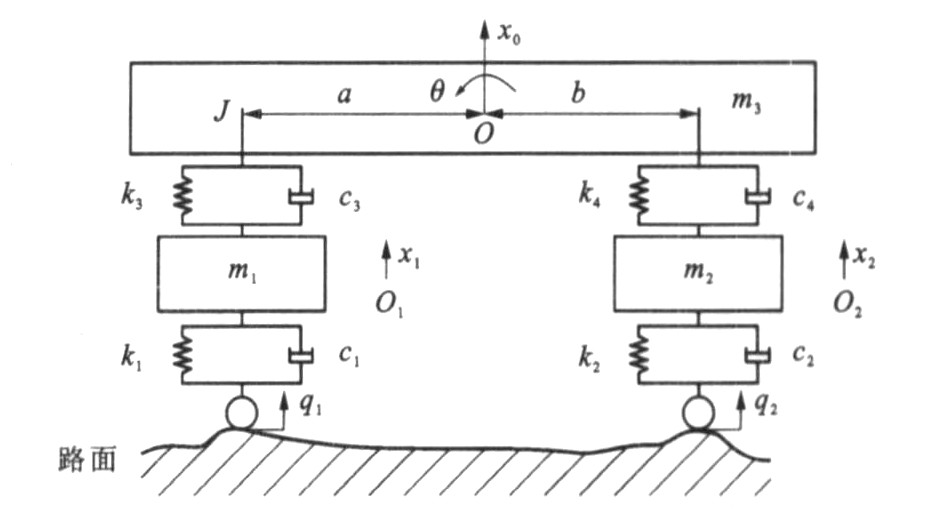
根据上述假设, 车辆模型就可以简化为4个自由度的平面模型。4个自由度分别为车身的垂直振动、俯仰振动和前后车轮的垂向振动。本文建立的二分之一车辆振动模型见图 2。

图  2  振动模型

Figure  2.  Vibration model

下载: 全尺寸图片 幻灯片

图 2中各参数意义: m₁、m₂分别为前后桥簧下质量; m₃为簧上质量; J为车身的转动惯量; a、b分别为前后桥到质心的距离; k₁、k₂分别为前后轮胎刚度系数; k₃、k₄分别为前后悬架刚度系数; c₁、c₂分别为前后轮胎阻尼系数; c₃、c₄分别为前后悬架阻尼系数; x₁、x₂分别为前后轴簧下质量垂向位移; x₀为车身质量垂向位移; θ为车身俯仰摆角; q₁、q₂分别为前后轮路面不平度激励。

根据图 2模型, 所建立的振动方程为

$\begin{array}{l}\mathit{{\rm M}}\stackrel{\cdot \cdot }{{\displaystyle \mathit{X}}}+\mathit{C}\dot{\mathit{X}}+\mathit{{\rm K}}\mathit{X}=\mathit{f}(3)\\ \mathit{{\rm M}}=\left[\begin{array}{cccc}m{}_1& & & \\ & m{}_2& & \\ & & m{}_3& \\ & & & J\end{array}\right]\\ \mathit{C}=\left[\begin{array}{cccc}c{}_1+c{}_3& 0& -c{}_3& ac{}_3\\ 0& c{}_2+c{}_4& -c{}_4& -bc{}_4\\ -c{}_3& -c{}_4& c{}_3+c{}_4& bc{}_4-ac{}_3\\ 0& 0& 0& a{}^{2}c{}_3+b{}^{2}c{}_4\end{array}\right]\\ \mathit{{\rm K}}=\left[\begin{array}{cccc}k{}_1+k{}_3& 0& -k{}_3& ak{}_3\\ 0& k{}_2+k{}_4& -k{}_4& -bk{}_4\\ -k{}_3& -k{}_4& k{}_3+k{}_4& bk{}_4-ak{}_3\\ 0& 0& 0& a{}^{2}k{}_3+b{}^{2}k{}_4\end{array}\right]\\ \mathit{f}=\left[\begin{array}{c}k{}_{1}q{}_1+c{}_1\dot{q}{}_1\\ k{}_{2}q{}_2+c{}_2\dot{q}{}_2\\ 0\\ 0\end{array}\right]\\ \mathit{X}=[x{}_{1}x{}_{2}x{}_0\theta ]{}^{\text{Τ}}\end{array}$

前后轮胎对路面的瞬时动载荷分别为

$\{\begin{array}{l}F{}_1(t)=k{}_1(q{}_1-x{}_1)+c{}_1(\dot{q}{}_1-\dot{x}{}_1)\\ F{}_2(t)=k{}_2(q{}_2+x{}_2)+c{}_2(\dot{q}{}_2+\dot{x}{}_2)\end{array}(4)$

由于F₁(t)和F₂(t)均为随机载荷, 前后轮胎动载荷的均方根值分别为

$\{\begin{array}{l}\sigma {}_{F{}_1}=\sqrt{\frac{{\displaystyle \sum _{i=1}^{{\rm N}}F}{}_1^2(t{}_i)}{{\rm N}}}\\ \sigma {}_{F{}_2}=\sqrt{\frac{{\displaystyle \sum _{i=1}^{{\rm N}}F}{}_2^2(t{}_i)}{{\rm N}}}\end{array}(5)$

式中: N为采样点总数。

前后轮的动载系数均方根值分别为

$\{\begin{array}{l}D{}_1=\sigma {}_{F{}_1}/\left(m{}_1+\frac{b}{a+b}m{}_3\right)g\\ D{}_2=\sigma {}_{F{}_2}/\left(m{}_2+\frac{a}{a+b}m{}_3\right)g\end{array}(6)$

3.   仿真分析

本文采用逐步积分法中的Runge-Kutta法进行微分方程数值求解, 用Matlab软件进行仿真, 选取2种型号标准双轴载重车作为参考对象^[7-8]。

车型一的结构参数如下: m₁、m₂、m₃分别为297、524、6 451 kg; J为46.25 kN·m²; a、b分别为3.79、2.31 m; k₁、k₂、k₃、k₄分别为788.10、875.67、198.25、1 138.37 kN·m^-1; c₁、c₂、c₃、c₄分别为2、2、15、15 kN·s·m^-1。

车型二的结构参数如下: m₁、m₂、m₃分别为700、1 000、15 950 kg; J为114.35 kN·m²; a、b分别为3.10、2.50 m; k₁、k₂、k₃、k₄分别为1 900、2 000、400、2 500 kN·m^-1; c₁、c₂、c₃、c₄分别为3、3、10、14 kN·s·m^-1。

车辆振动系统的固有频率分布在0.7~15.0 Hz^[9], 常用车速为10~50 m·s^-1。若取地面作用于轮胎的激励时间频率下限f₁为0.5 Hz, 上限f₂为30.0 Hz^[9], 那么对应的空间频率的上下限ϕ₂、ϕ₁分别为3.00、0.01 m^-1。只需在这个空间频率范围内仿真便可覆盖车辆振动系统的固有频率, 所得结论符合真实情况。

3.1   路面等级对轮胎动载的影响

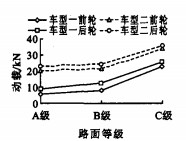
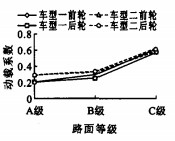
2种车型以30 m·s^-1速度分别行驶在A、B、C级路面上, 通过仿真计算得前后轮动载均方根及动载系数与路面等级的关系, 见图 3、4。

图  3  载与路面等级关系

Figure  3.  Relationship between dynamic load and road grade

下载: 全尺寸图片 幻灯片

图  4  载系数与路面等级关系

Figure  4.  Relationship between dynamic load coefficient and road grade

下载: 全尺寸图片 幻灯片

从图 3、4可看出, 在不同等级路面上行驶时, 后轮产生的动载均大于前轮产生的动载。随着从A级到C级路面等级的降低, 路面不平度加剧, 车辆对路面作用的动载不断加大, 动载系数也随着增大。由于前桥静载明显小于后桥静载, 故前轮的动载系数要大于后轮的动载系数。

3.2   车速对轮胎动载的影响

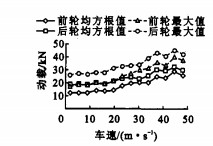
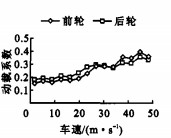
为了研究重型车辆的车速对车辆动载及动载系数的影响, 本文选用车型二和A级路面作为仿真基础。根据系统模态分析可得车型二的4阶固有频率ω₁、ω₂、ω₃、ω₄分别为9.41、13.05、57.36、67.74 rad·s^-1, 并可求得对应于系统4阶固有频率下的车速取整后分别为6、8、38、45 m·s^-1。通过仿真计算可得轮胎动载均方根、最大动载及动载系数随车速变化规律, 见图 5、6。

图  5  载与车速关系

Figure  5.  Relationship between dynamic dynamic load and vehicle speed

下载: 全尺寸图片 幻灯片

图  6  动载系数与车速关系

Figure  6.  Relationship between load coefficient and vehicle speed

下载: 全尺寸图片 幻灯片

从图 5、6中可看出, 随着车速的提高, 前后轮的动载荷均近似成线性关系增大。通过比较动载均方根值与最大值可发现, 两者变化趋势基本一致。另外当车速对应于或接近车辆固有频率时, 车轮动载比较大, 特别是以对应高阶固有频率的车速行驶时, 动载和动载系数均出现有小峰值的现象, 这说明了车辆固有特性对轮胎动载的影响。

3.3   载质量对轮胎动载的影响

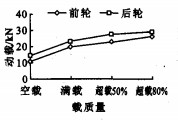
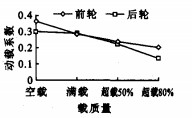
现以A级路面作为基础, 车型二以30 m·s^-1速度行驶其上, 比较在空载、满载、超载情况下(超载率分别取为50%、80%)^[9]的车辆对轮胎动载的影响, 见图 7、8。

从图 7、8可见, 随着载质量的增大, 车辆行驶时对路面的动载在增大, 而动载系数在减小, 这说明空车的振动比重车较为激烈, 其动载系数较大。重载和超载车辆由于轴载大, 其动作用力明显大于空车, 再加上车辆静载荷, 其作用于路面的总载荷仍远大于空车, 这说明重载车辆对路面的损伤要大于空车, 限制超载是提高高等级公路使用寿命的主要措施。

图  7  动载与载质量关系

Figure  7.  Relationship between dynamic load and loading capacity

下载: 全尺寸图片 幻灯片

图  8  动载系数与载质量关系

Figure  8.  Relationship between dynamic load coefficient and loading capacity

下载: 全尺寸图片 幻灯片

3.4   车辆参数对轮胎动载的影响

为了研究车辆结构参数对动载荷的影响, 选用A级路面为基础, 车型一以30 m·s^-1速度在其上行驶, 改变其中某一参数时, 其他各参数均保持不变, 以观察该参数对动载的影响规律。

3.4.1   轮胎刚度对轮胎动载的影响

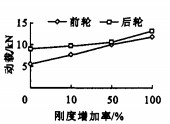
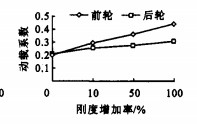
为了对不同轮胎刚度下的轮胎动载进行研究, 将前后轮胎刚度均增加10%、50%、100%, 仿真得到3种情况下的轮胎动载和动载系数与轮胎刚度的关系曲线, 见图 9、10。

图  9  载与轮胎刚度关系

Figure  9.  Relationship between dynamic load and tire stiffness

下载: 全尺寸图片 幻灯片

图  10  载系数与轮胎刚度关系

Figure  10.  Relationship between dynamic load coefficient 8nd tire stiffness

下载: 全尺寸图片 幻灯片

由图 9、10可知, 轮胎刚度的增大会引起前后轮胎动载和动载系数的增大。由于轮胎刚度与充气压力是紧密相关的, 充气压力的增大会引起轮胎刚度的增大, 从而导致车辆对路面动作用力的增大。目前为了避免高速公路的早期破坏, 应限制高压轮胎的使用。

3.4.2   车辆悬架阻尼对轮胎动载的影响

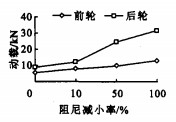
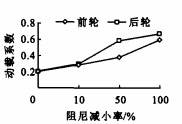
车辆悬架刚度和阻尼都会对轮胎动载造成一定影响, 但目前国内由于载重汽车(尤其是自主开发的重型车)广泛采用的悬架形式仍为钢板弹簧, 这种悬架的刚度因要考虑其他设计要素而不能随意变化, 因此, 本文仅研究悬架阻尼变化的影响。对不同悬架阻尼下的轮胎动载进行研究, 将后悬架阻尼分别降低10%、50%、100%, 得到3种情况下的前后轮胎动载和动载系数, 仿真结果见图 11、12。

图  11  动载与阻尼关系

Figure  11.  Relationship between dynamic load and damping

下载: 全尺寸图片 幻灯片

图  12  动载系数与阻尼关系

Figure  12.  Relationship between dynamic load coefficient and damping

下载: 全尺寸图片 幻灯片

由图 11、12可知, 悬架阻尼减小, 车辆的垂向振动必然加剧, 而后轮的增加更为明显, 振动加剧导致轮胎对路面的动载作用增大。可见, 为了减小车辆对路面的动作用力, 应选择合理的悬架阻尼参数。

4.   结语

(1) 建立了4个自由度的二分之一车辆振动模型, 采用随机路面谱研究了路面等级、车速、载质量以及车辆参数对轮胎动载的影响。

(2) 路面承受的动载直接取决于路面的平整度, 平整度较好的路面所承受的动载较小。

(3) 车辆动载荷和动载系数随着车速的提高而增大, 其最大值与均方根值变化规律一致, 而且在固有频率下行驶时会出现峰值现象, 这种关系可为今后路面设计提供参考。

(4) 随着载质量的增大, 动载系数有所降低, 而动载荷有所增大, 说明重载车辆对路面的损坏远大于空载车辆, 因此, 应严格限制超载现象。

(5) 增大轮胎刚度系数和减小悬架阻尼系数都会引起车辆动载荷、动载系数的增大, 在现实中应限制高压轮胎的使用和选择合理的车辆阻尼参数。