Estimation models of distribution functions for travel time value with maximum entropy principle
Article Text (Baidu Translation)
-
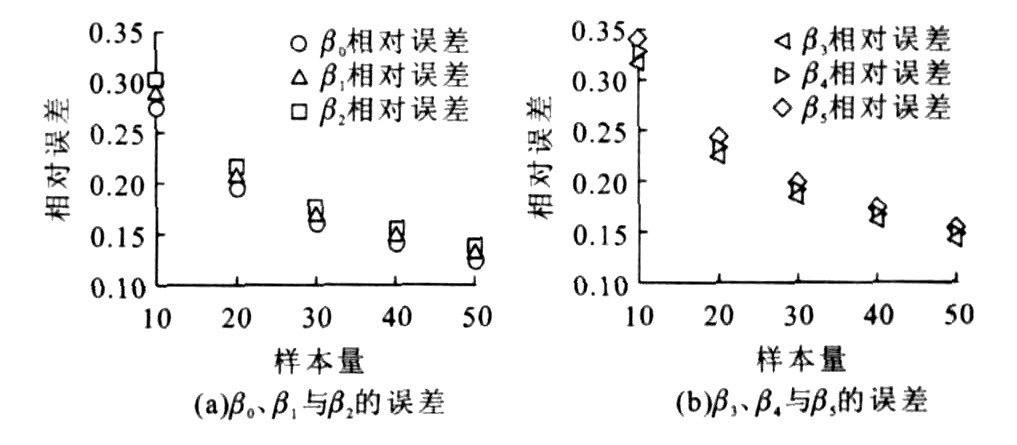
摘要: 为提高使用时间价值数据拟合其统计分布的精度, 将最大熵原理分别与低阶(≤6)经典矩和概率加权矩相结合, 建立了时间价值低阶经典矩与概率加权矩统计分布函数模型。仿真结果表明: 在大样本量下, 利用经典矩与概率加权矩对参数估计的精度相当, 在小样本量下(< 30), 采用概率加权矩估计参数的相对误差在10%~35%之间, 而采用经典矩估计参数的相对误差在20%~80%之间。可见利用概率加权矩克服了经典矩模型在小样本量下参数估计的大偏差问题, 且利用其可以准确地预测交通方式分担率与分析交通定价政策对交通行为的影响。Abstract: In order to improve the goodness-of-fit accuracy of statistical distribution for travel time value with its stylebook data, maximum entropy principle was combined with probability-weighted moments (PWM) and statistical ordinary moments (SOM)(≤6) respectively, two new statistical distribution models were proposed, and parameter estimation was carried out by using probability-weighted moments and statistical ordinary moments. Simulation result shows that when the number of stylebooks is less than 30, the average relative errors between exact values and estimating values range from 10% to 35% and from 20% to 80% respectively, but the statistical accuracies are similar on large sample size condition, so the estimating accuracy with probability-weighted moments is higher. Obviously, the proposed methods are useful to promote parameter estimating accuracy, may predict the split ratios of traffic modes effectively, and analyze the influence of transportation pricing policy on travel behaviors.
-
[1] Beesley ME. The value of time spent in traveling: some new evidences[J]. Economical, 1965, 32: 174-185. doi: 10.2307/2552547 [2] Deserpa A C. A theory of the economics of time[J]. The Economic Journal, 1971, 81(4): 828-845. [3] Hensher D A. A probabilistic disaggregate model of binary mode choice[R]. Melbourne: Australian Road Research Board, 1974. [4] Forsyth PJ. The value of time in an economy with taxation[J]. Journal of Transport Economics and Policy, 1980, 14(3): 337-362. [5] Small K. The scheduling of consumer activities: work trips[J]. American Economic Review, 1982, 72(3): 467-479. [6] Hensher D, Milthorpe F, Smith N, et al. Urban tolled roads and the value of travel time savings[J]. Economic Record, 1990, 6(2): 146-156. [7] Hensher D A. Measurement of the valuation of travel time savings[J]. Journal of Transport Economics and Policy, 2001, 35(1): 71-98. [8] Wardman M. A review of British evidence on time and service quality valuations[J]. Transportation Research Part E, 2001, 37(2): 107-128. [9] Jovicic G, Hansen C O. A passenger travel demand model for Copenhagen[J]. Transportation Research Part A, 2003, 37(2): 333-349. [10] Brownstone D, Small K A. Valuing time and reliability: assessing the evidence from road pricing demonstrations[J]. Transportation Research Part A, 2005, 39(4): 279-293. [11] 周伟. 旅客时间价值[J]. 交通运输工程学报, 2003, 3(3): 110-116. doi: 10.3321/j.issn:1671-1637.2003.03.025Zhou Wei. Time value of passengers[J]. Journal of Traffic and Transportation Engineering, 2003, 3(3): 110-116. (in Chinese) doi: 10.3321/j.issn:1671-1637.2003.03.025 [12] 仝允恒. 城市快速交通线项目的最优票价与政府补偿[J]. 系统工程理论与实践, 2001, 21(4): 88-91. doi: 10.3321/j.issn:1000-6788.2001.04.018Tong Yun-huan. Optimal fare pricing for urban rapid transport line project and government compensation[J]. Systems Engineering—Theory and Practice, 2001, 21(4): 88-91. (in Chinese) doi: 10.3321/j.issn:1000-6788.2001.04.018 [13] 俞礼军, 严海, 严宝杰. 最大熵原理在交通流统计分布模型中的应用[J]. 交通运输工程学报, 2001, 1(3): 91-94. doi: 10.3321/j.issn:1671-1637.2001.03.023Yu Li-jun, Yan Hai, Yan Bao-jie. Maximum entropy method and its application in probability density function of traffic flow[J]. Journal of Traffic and Transportation Engineering, 2001, 1(3): 91-94. (in Chinese) doi: 10.3321/j.issn:1671-1637.2001.03.023 [14] Greenwood J A, Landwehr J M, Matalas N C. Probability weighted moments: definition and relation to parameters of several distributions expressible in inverse form[J]. Water Resources Research, 1979, 15(5): 49-54. [15] Pandey M D. Direct estimation of quantile functions using the maximum entropy principle[J]. Structural Safety, 2000, 22(1): 61-79. doi: 10.1016/S0167-4730(99)00041-7 [16] Shore H. Simple approximations for the inverse cumulative function, the density function and the loss integral of the normal distribution[J]. Applied Statistics, 1982, 31(2): 108-114. doi: 10.2307/2347972 [17] HoskingJ R M, Wallis J R. Regional Frequency Analysis[M]. UK: Cambridge University Press, 1997. [18] Hosking J R M. Parameter and quantile estimation for the generalized Pareto distribution[J]. Tecnometrics, 1987, 29(3): 39-49. [19] Jaynes E T. Information theory and statistical mechanics Ⅰ[J]. Physical Review, 1957, 106(4): 620-630. doi: 10.1103/PhysRev.106.620 [20] Jaynes E T. Information theory and statistical mechanics Ⅱ[J]. Physical Review, 1957, 108(2): 171-190. doi: 10.1103/PhysRev.108.171 [21] Kadane J B. A moment problem for order statistics[J]. The Annals of Mathematical Statistics, 1971, 42(2): 45-51. [22] MallowsCL. Boundsondistributionfunctionsintermsof expectations of order statistics[J]. The Annals of Probability, 1973, 1(2): 297-303. [23] Shannon C E. A mathematical theory of communication[J]. Bell System Technology Journal, 1948, 27(4): 379-423. [24] Shore J E, Johnson R W. Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy[J]. IEEE Transact Information Theory, 1980, 26(1): 26-37. doi: 10.1109/TIT.1980.1056144 [25] Wu N. The Maxi mum Entropy Method[M]. Berlin: Springer-Verlag, 1997. -





 下载:
下载: