Crossing aerodynamic force analysis of tarpaulin for trains
-
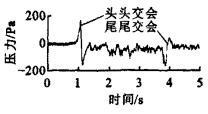
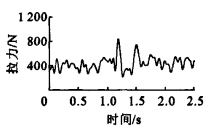
摘要: 为解决目前一车苫盖2张货车篷布(简称X型篷布) 存在的严重兜风现象与货物湿损问题, 并检验新型篷布(简称D型篷布) 的使用效果, 基于不同装载与加固方案, 通过实车试验, 针对D型篷布与X型篷布在有绳网和无绳网12种情况下, 测试了列车交会压力波和货车蓬布绳索拉力。测试结果表明: 当80~120km·h-1速度下的货车与200~210km·h-1速度下的动车组交会时, 动车组上感受的最大压力波幅值仅为577Pa, 货车感受到的最大压力波幅值为715Pa; 绳索最大值为1055N, 出现在无网X型篷布的角绳上, 满足相关规定要求; 没有苫盖篷布绳网时, 2种篷布兜风现象均较严重, 同等速度下无绳网X型篷布逆向压缝篷布绳索拉力比顺向压缝的大40%左右; 篷布绳网在降低篷布绳索气动力中发挥了重要作用, 大部分工况下无绳网篷布绳索受到的气动力比有网的大50%~80%。可见, 在相同工况下, D型篷布比X型篷布使用性能优良。Abstract: In order to solve catching wind badly and goods being soaked and damaged easily for two-piece freight tarpaulin (X-type tarpaulin), and to test the using effect of new freight tarpaulin (D-type tarpaulin), defferent loading and reinforcing projects were considered, twelve using conditions with and without cord net were confirmed, the crossing pressure waves of trains and the tensile forces of tarpaulin cord and net cord were tested by full-scale train test.The result shows that when freight car at 80~120 km·h-1 passes by multiple unites at 200~210 km·h-1, the maximal magnitudes of air pressure waves are 577 Pa and 715 Pa separately for multiple unites and freight car; the maximal tensile force of cord is 1 055 N, and it appears at the corner cord of X-type tarpaulin without net, which satisfies the demand of correlative standards; catching wind of two kinds of tarpaulins without net is seriously, and at the same speed, the tensile force of X-type tarpaulin against wind is about 40% greater than that down wind; cord net has an important role, and the tensile force of cord without net is 50%~80% greater than that with net.Thus, D-type tarpaulin has better using performance than X-type tarpaulin under the same instance.
-
复合式混凝土路面和混凝土路面加铺层在国外已有数十年的应用历史, 中国从20世纪80年代末开始应用, 1994年颁布的行业标准“公路水泥混凝土路面设计规范”[1]已将这两种结构类型纳入。复合式混凝土路面通常为两层不同强度或不同类型的混凝土复合而成的水泥混凝土路面结构; 混凝土路面加铺层是指为提高原有水泥混凝土路面的承载能力和(或) 改善表面功能而在其上加铺的水泥混凝土面层, 从结构的力学特征来看, 它们均可视为弹性地基上双层板。
双层水泥混凝土路面设计理论、方法和参数的研究较普通单层的水泥混凝土路面的研究薄弱很多, 尚存在一些有待完善和改进之处, 尤其是在双层水泥混凝土路面板的温度应力方面。由于上下层混凝土强度或类型的不同, 以及层间接触状况的影响, 双层水泥混凝土路面板的温度应力计算较为复杂, 迄今尚未得到很好的解决。在现行的设计规范[1]中, 复合式混凝土路面的温度应力尚未计入; 混凝土路面加铺层的温度应力的计算过于粗略, 误差较大。
1. 基本假设和温度应力的构成
双层水泥混凝土路面板(以下简称双层板) 温度应力的分析基于如下5个基本假设:
(1) 双层板的弯曲是小挠度的, 即板截面竖向拉压和水平剪切变形可以忽略, 且四边自由;
(2) 双层板层间竖向连续, 无夹层, 也无脱空和嵌入现象;
(3) 双层板均为等截面且材料各向同性;
(4) 板的翘曲变形可视为x, y方向翘曲变形的叠合;
(5) 下层板板底与地基竖向连续, 水平向光滑接触无摩阻力。
双层板的温度应力是受到板本身, 上下板变形协调以及地基对温度变形的约束引起的, 它可分解为3个部分: 由于温度沿板厚方向非线性分布引起的内应力σa; 上下层板变形协调约束引起板间约束应力σb和地基约束引起的温度翘曲应力σc。双层板的温度沿板厚方向非线性分布引起的温度内应力σa和地基约束引起的温度翘曲应力σc在概念和解法上与单层板的相同, 在此不再一一列出。以下讨论双层板间变形约束协调引起的温度层间约束应力和应变。
2. 不计板间及地基约束的温度应变
沿路面深度呈非线性分布的路面结构温度场tp (τ, z) (图 1(a)), 上下层板的温度状况可用上下层板各自的平均温度t′i和温度梯度, tgi (i=1, 表示上层板, i=2表示下层板, 下同) 描述(图 1(b))。t′i, tgi的计算式为
t′1=1/h1∫h10tp(τ,z)dzt′2=1/h2∫h20tp(τ,h1+z)dz} (1)tg1=6t1/h1-12/h31∫h10tp(τ,z)zdztg2=6t2/h2-12/h32∫h20tp(τ,h1+z)zdz} (2)
式中: h1为板厚度; τ为时刻(h)。
由上述温度状况引起的上下层板截面的温度应变平均值和斜率(应变梯度) 相应为εi和εgi (图 2(a)), 其中, 温度应变梯度可等效地表示为受到一虚拟弯矩Mi作用的情况(图 2(b))。还可视为截面平均应变为ε′i, 且有虚拟轴向力Ni作用的情况(图 2(c))。εi、εgi、Mi和Ni的表达式为
εi=αitiεgi=αitgi (3)
Mi=αitgiDiNi= (ε′i-εi) Eihi (4)
式中: αi为板混凝土热膨胀系数; ti为以上层板混凝土硬化时板截面平均温度t0i为起点的板平均温度增量, 即ti=t′i-t0i; Di=Eih 3i /12为板的弯曲刚度; Ei为混凝土弹性模量, 若处于板中部平面应变状况, 则Ei应改为Ei*, Ei*=Ei/ (1-μi), μi为泊松比。
3. 板间约束应变和应力
根据本文的基本假设, 可以推定上下层板中性面的挠曲方程相同, 上下层板具有相同的弯曲曲率, 即上下层的应变梯度相同, 这一应变梯度可称为双层板的综合温度应变梯度, 记作εg。
在双层板层间水平方向光滑无摩阻状态下, 上下层板弯曲中性面位于各自的中面。双层板的总弯曲刚度为上下层板刚度之和, 即Dg=D1+D2。上下板截面上作用的虚拟弯矩M1和M2引起双层板综合温度应变梯度εg为(图 3(a))
εg= (α1tg1D1+α2tg2D2) / (D1+D2) (5)
当层间为结合状态, 上下层板在层间无相对水平位移, 即ε′1=ε′2=ε0。双层板平均应变ε0和轴向力Ni表达式
ε0=e(α1t1/E2h2+α2t2/E1h1) (6)Ν1=-Ν2=e(α1t1-α2t2) (7)
式中: e= (1/E1h1+1/E2h2)-1, 其物理意义为双层板截面相对抗拉刚度。
在层间结合状态下, 上下层板截面具有同一弯曲中性面, 它与上下层板中面的距离hs和hx为
hs=eh0/2E1h1;hx=eh0/2E2h2 (8)
式中: h0=h1+h2为双层板总厚度。
这时双层板截面受到的总弯矩Mg和截面弯曲总刚度Dg分别为
Μg=Μ1+Μ2+Ν1h0/2 (9)Dg=D1+D2+D3‚ D3=eh0/4 (10)
双层板的综合温度应变梯度εg则为(图 3(b))
εg= (α1tg1D1+α2tg2D2+2D3 (α1t1-α2t2) /h0) / (D1+D2+D3) (11)
在层间接触条件从光滑向结合过渡中, 上下层板的中性面从光滑状态的各自中面向结合状况的同一中性面等比例过渡, 其比例系数ku可称为层间结合系数。当ku=0, 层间为光滑状态, ku=1为结合状态, 0 < ku < 1称为半结合状态。在此作类似的推广, ε′1和ε′2从光滑状况的ε1和ε2向结合状况的ε0过渡的增量Δε1和Δε2仍然与ku成正比, 即
Δε1=ε′1-ε1=-eku/E1h1(α1t1-α2t2)Δε2=ε′2-ε2=eku/E2h2(a1t1-α2t2)} (12)
上下层板截面的轴向力Ni, 双层板截面的总弯矩Mg以及总刚度Dg分别为
Ν1=-Ν2=e(α1t1-α2t2)ku (13)Μg=Μ1+Μ2+Ν1h0/2Dg=D1+D2+D3ku (14)
由此可得到半结合式双层板的综合温度应变梯度εg为(图 3(c))
εg= (α1tg1D1+α2tg2D2+2D3 (α1t1-α2t2) ku/h0) /
(D1+D2+D3ku) (15)
式(12) 和式(15) 分别为不同层间接触状况的上下层板平均温度应变和双层板综合温度应变梯度的统一式, ku=0为光滑状况, ku=1为结合状况, ku在0~1之间则为半结合状况。由此可方便地推出由层间变形协调条件引起的双层板温度约束应力σb的计算式如下
σb={E1[Δε1+α1tg1(z-h1/2)-εg(z-h1/2-hsku)]z∈[0,h)E2[Δε2+α2tg2(z-h1-h2/2)-εg(z-h1-h2/2+hxku)]z∈(h1,h1+h2] (16)
4. 板间约束应变分析
在无隔温度夹层或层间脱空的条件下, 双层板温度场与普通单层混凝土路面的温度场基本相同。按现行规范采用的路表温度拟合规律, 在无云晴天双层水泥混凝土路面的温度场tp (τ, z) 可表示为[2]
tp(τ,z)=t′m+thl/2e-βzsin(ωτ+βz) (17)
式中: t′m为路表日平均温度(℃); thl为路表温度的日较差(℃); ω=π/12 (rad/h); β= (ω/2λ)0.5, λ为上层板混凝土的导热系数, 若下层板的导热系数λ′与λ差异较大, 则在应用式(17) 时, 下层板的厚度当量为(λ′/λ) h2。
将式(17) 的双层板温度场tp (τ, z) 代入式(1) 和式(2), 并假设上下层板的导热系数相同, 得到上下层板的平均温度t′1, t′2和温度梯度tg1, tg2为


式中: ft、fg、ξt、ξg为βh的函数(图 4), 下标1表示βh1, 下标2表示βh2。
由于上层板的蔽盖, 下层板的平均温度t′2的日较差增量和温度梯度tg2的最大值为相同板厚的上层板的e-βh1倍, 出现最大值的相位角与相同板厚的上层板的相位角滞后βh1 (rad)。ft和fg均随着βh的增大而减小, 其中fg的减小速率稍大于ft的; 而ξt和ξg则随着βh的增大而增大, 无论βh为何值, ξt/π > 0.5, 也就是说板平均温度的最大值出现时刻总是迟于路表温度最大值出现时刻; 在βh较小时, ξg/π < 0.5, βh较大时, ξg/π > 0.5, 其分界点在βh=1.95左右, 这说明, 板的温度梯度tg的最大值在βh较小时, 先于路表温度最大值出现, 而βh较大时, 则滞后于路表温度最大值出现时刻。
将式(18) 代入式(12), 整理得到上下层板中性面的应变增量Δε1和Δε2为
Δε1=-eku/{E1h1[ (α1tm1-α2tm2) +th1/2Atcos (ωτ-ζt) ]}
Δε2=eku/{E2h2[ (α1tm1-α2tm2) +th1/2Atcos (ωτ-ζt) ]} (19)
At=α1ft1cos (ζt-ξt1) -α2ft2e-βh1cos (ζt-ξt2-βh1)
ζt=arctg[α1ft1sinξt1-α2ft2e-βh1sin(ξt2+βh1)α1ft1cosξt1-α2ft2e-βh1cos(ξt2+βh1)]tmi=t′m-t0i
将式(18) 代入式(15), 整理得到双层板温度应变梯度εg的表达式如下
εg=2 (α1tm1-α2tm2) D3ku/h0Dg+th1/[2βAgcos (ωτ-ζg) ] (20)
Ag=[ag1cos (ζg-ξt1) +ag2cos (ζg-ξt2-βh1) +ag3cos (ζg-ξg1) +ag4cos (ζg-ξg2-βh1) ]/Dg
ζg=arctg[ag1sinξt1+ag2sin (ξt1+βh1) +ag3sinξg1+
ag4sin (ξg2+βh1) ]/[ag1cosξt1+ag2cos (ξt1+βh1) +
ag3cosξg1+ag4cos (ξg2+βh1) ]
ag1=2α1ft1D3ku/βh0, ag2=-2α2ft2e-βh1D3ku/βh0,
ag3=α1fg1D1, ag4=α2e-βh1fg2D2
从式(19) 和式(20) 中可以看到, 双层板层间约束条件引起双层板综合温度应变梯度εg和上下层板原中面约束应变增量Δε1和Δε2由二部分组成: 第一部分由上下层板热膨胀系数差异(α1tm1-α2tm2) 引起的; 第二部分是由温度的日较差th1产生的。第一部分温度应变一般是不考虑的, 原因有2个: ①相同的水泥和骨料的情况下, 不同强度和不同类型的混凝土热膨胀系数差异一般不大; ②欲想正确地估计混凝土初始温度t0i极为困难, 另外, 必须弄清温度变化的路径, 混凝土在缓慢应变下的力学性质, 如蠕变和松驰等。
若不计α1和α2的差异或α1=α2, 则双层板的温度应变梯度εg和上下层板中性面的应变增量Δε1和Δε2可改为双层板的综合温度梯度tg, 以及上下层中性面的等效温度增量t1和t2, 它们日变化均为一余弦波, 即在式(19) 和式(20) 中剔除α1和α2即可。
5. 结语
(1) 双层板的温度应力由温度沿板厚非线性引起的内应力, 上下层板变形约束引起的板间约束应力和地基约束引起的温度翘曲应力三部分组成。
(2) 采用层间结合系数ku表征双层板间接触状况时, 双层板综合温度梯度εg和上下层板原中面的温度约束应变增量ε′1和ε′2的计算式可统一为式(15) 和(12)。
(3) 上下层板的平均温度梯度和板中面平均温度的计算方法同单层板, 下层板的平均温度梯度和板面平均温度的最大值为相同板厚的层板的最大值的e-βh1倍, 最大值的相位角滞后βh1 rad。
(4) 在路表温度采用正弦函数拟合时, 上下层板的平均温度、温度梯度、上下层板的综合温度应变梯度、原中面的温度应变增量随时间的变化规律均为一个简谐函数。
-
表 1 交会空气压力波幅值
Table 1. Magnitudes of crossing pressure waves
序号 速度/ (km·h-1) 交会压力波幅值/Pa 动车组 货车 动车组 敞车 D型蓬布 X型蓬布 1 200 79 235 503 335 319 2 199 101 391 527 342 350 3 200 120 560 541 365 354 4 205 117 577 644 376 394 5 210 118 548 715 434 427 表 2 绳索的最大拉力
Table 2. Maximal tensile forces of tarpaulin cords
序号 速度/ (km·h-1) 篷布绳索最大拉力/N D型 X型 动车组 货车 无网 有网 无网 有网 1 200 79 591 295 604 335 2 199 101 680 392 722 448 3 200 120 804 412 926 613 4 205 117 610 239 858 694 5 210 118 789 372 1 055 710 表 3 D型篷布绳索拉力平均值比较
Table 3. Average value comparison of D-type tarpaulin cord
序号 车型与速度/ (km·h-1) D型篷布绳索拉力平均值/N 无网 有网 动车组 货车 超车帮大于1 m 不超车帮 超车帮小于1 m 超车帮小于1 m 不超车帮 超车帮小于1 m 1 200 79 350 352 334 172 185 163 2 199 101 416 427 380 196 206 185 3 200 120 458 478 429 209 225 199 4 205 117 445 469 432 194 208 187 5 210 118 444 468 434 196 216 185 表 4 X型篷布绳索拉力平均值比较
Table 4. Average value comparison of X-type tarpaulin cord
序号 车型与速度/ (km·h-1) X型篷布绳索拉力平均值/N 无网 有网 动车组 货车 超车帮大于1 m 不超车帮 超车帮小于1 m 超车帮小于1 m 不超车帮 超车帮小于1 m 1 200 79 217 227 210 148 157 140 2 199 101 247 258 236 165 176 160 3 200 120 280 286 274 187 199 179 4 205 117 274 285 266 181 199 174 5 210 118 273 292 260 182 196 171 -
[1] Toshiaki Imai, Toshishige Fujii, Katsuji Tanemoto. Newtrain regulation method based on wind direction and velocity of natural wind against strong winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 90 (12): 1601-1610. [2] 刘呈坤, 马建伟. 浅论蓬盖布的结构与性能要求[J]. 化纤与纺织技术, 2005, 34 (1): 38-40.Liu Cheng-kun, Ma Jian-wei. Simple discussion on the structure and performance requirment of covering cloth[J]. Chemical Fiber and Textile Technology, 2005, 34 (1): 38-40. (in Chinese) [3] 张兴国, 张超. 铁路货车蓬布调度管理系统的研究与实现[J]. 铁路计算机应用, 2003, 12 (2): 7-10.Zhang Xing-guo, Zhang Chao. Research and implementation of traffic control and management system for rail way freight trapaulin[J]. Rail way Computer Application, 2003, 12 (2): 7-10. (in Chinese) [4] 董秀洁, 周光辉. 涤纶篷布用抗静电剂生产工艺自控系统[J]. 纺织学报, 2006, 27 (4): 102-104.Dong Xiu-jie, Zhou Guang-hui. Automatic control system for the production process of antistatic agent for polyester tent fabrics[J]. Journal of Textile Research, 2006, 27 (4): 102-104. (in Chinese) [5] 赵紫红. 铁路货车篷布管理存在问题的分析与建议[J]. 铁道货运, 2006, 24 (9): 31-33.Zhao Zi-hong. Analysis and suggestion for the management of freight tarpaulin[J]. Railway Freight Transport, 2006, 24 (9): 31-33. (in Chinese) [6] 聂建忠, 奇平. 对改进货车篷布规格和加固方法的探讨[J]. 铁道货运, 2003, 21 (5): 12-13.Nie Jian-zhong, Qi Ping. Discussion for the development of size and reinforcement of the freight tarpaulin[J]. Rail way Freight Transport, 2003, 21 (5): 12-13. (in Chinese) [7] 刘堂红, 田红旗, 梁习锋. "长白山"高速列车与货车交会试验研究[J]. 中国铁道科学, 2006, 27 (3): 56-61.Liu Tang-hong, Tian Hong-qi, Liang Xi-feng. Test research on Changbaishan high-speed train passing by freight car[J]. China Rail way Science, 2006, 27 (3): 56-61. (in Chinese) [8] 田红旗, 梁习锋, 刘堂红, 等. 京秦线提速200公里/小时列车交会综合试验研究报告[R]. 长沙: 中南大学, 2005. [9] 田红旗, 梁习锋, 刘堂红, 等. 蓬布、蓬布网绳和蓬布绳索试验研究报告[R]. 长沙: 中南大学, 2006. -






 下载:
下载:




 下载:
下载: