0.   引言

车辙是沥青路面最常见的破坏形式之一, 不仅影响车辆行驶的舒适性, 严重时还影响行车安全^[1]。国外的沥青路面设计主要通过2种方法控制路面的过量车辙: 一是控制路基顶面的压应变小于容许压应变; 二是采用分层总和法直接计算路表的车辙。可以预见, 采用以上2种方法之一控制路表的车辙将是中国沥青路面设计方法必然的发展方向。

目前国外路基顶面容许压应变与标准轴载(80 kN)作用次数之间的关系式是基于AASHTO试验路的观测资料建立的^[2], 缺乏理论基础, 而且中国的沥青路面结构和标准轴载与国外相差很大, 因此, 必须专门建立适合中国国情的路基顶面容许压应变公式。另外, 邱延峻等认为路基的永久变形不仅影响路表的车辙, 同时还对路面的开裂有着非常重大的影响, 故展开了路基顶面容许永久变形的研究^[3-4]。

建立适合中国国情的路基顶面容许压应变公式, 计算路基顶面永久变形, 或采用分层总和法计算路表的车辙, 均需要路基土永久变形预估模型, 因此, 研究路基土的永久变形特性对于完善中国的沥青路面设计方法具有重要意义。

1.   路基土永久变形国内外研究现状

路基土永久变形领域开创性的工作首推Monismith等对粉质粘土进行三轴重复加载试验, 提出指数模型来预测路基土的永久变形^[5]

$\epsilon {}_{\text{p}}=A{\rm N}{}^b(1)$

式中: ε_P为塑性应变; N为荷载作用次数; A、b为材料参数。

随后, 很多学者对路基土永久变形特性展开试验研究, 先后建立了双曲线模型^[6]、VESYS模型^[7]、屈服面模型^[8]与Shakedown模型^[9-11]等。Tseng和Lytton利用重复加载试验对粒料和路基土建立的永久变形预估模型^[12]为

$\frac{\overline{\epsilon }{}_{\text{p}}}{\epsilon {}_{\text{r}}}=\beta {}_{\text{r}1}\left(\frac{\epsilon {}_0}{\epsilon {}_{\text{r}}}\right)\text{e}{}^{-\left(\frac{\rho }{{\rm N}}\right){}^{\beta }}(2)$

式中: ε₀、β和ρ为材料参数; ε_r为测定材料参数时所施加的回弹应变; β_r1为修正系数; $\overline{\epsilon }{}_{\text{p}}$为亚层内平均塑性应变。

针对路基土, Tseng和Lytton对式(2)中的系数进行回归得到了如下公式^[12]

$\{\begin{array}{l}\lg \left(\frac{\epsilon {}_0}{\epsilon {}_{\text{r}}}\right)=-1.69867+0.09121W{}_{\text{c}}-\\ 0.0172893\sigma {}_{\text{d}}+0.91219\lg (E{}_{\text{r}}/6.895)\\ \lg (\beta )=-0.9730-0.0000040319072W{}_{\text{c}}^2\sigma {}_{\text{d}}+\\ 0.0024894851\sigma {}_{\text{d}}-0.000004902103W{}_{\text{c}}^2\sigma {}_{\theta }\\ \\ \lg (\rho )=11.009+0.00009862219W{}_{\text{c}}^2\sigma {}_{\text{d}}-\\ 0.0583901\sigma {}_{\text{d}}+0.0000079042785W{}_{\text{c}}^2\sigma {}_{\theta }\end{array}(3)$

式中: W_c为含水量, %;σ_d为偏应力, kPa; σ_θ为体积应力, kPa; E_r为动回弹模量, kPa。

Tseng和Lytton建立的永久变形模型是非线性的。对该模型进行的大量研究表明, 根据该模型得到的永久变形存在一些明显不合理的发展趋势^[13]。例如, 在多数情况下, 当路基的回弹模量增加, 而其他设计参数不变时, 路基的车辙量也增加。

Ayres对Tseng和Lytton模型进行了改进, 塑性应变和弹性应变间的关系式仍为式(2), 但系数回归公式中去掉了体积应力和偏应力项^[14]

$\{\begin{array}{l}\lg \left(\frac{\epsilon {}_0}{\epsilon {}_{\text{r}}}\right)=0.74168+0.08109W{}_{\text{c}}-0.000012157E{}_{\text{r}}\\ \lg (\beta )=-0.61119-0.017638W{}_{\text{c}}\\ \lg (\rho )=0.622685+0.541524W{}_{\text{c}}\end{array}(4)$

根据式(4)计算出的ε₀/ε_r还要乘以一个调整系数F_Adj。当E_r/1 000≥2时, F_Adj为

$F{}_{\text{A}\text{d}\text{j}}=1.2-1.39\text{e}{}^{-0.058E{}_{\text{r}}/1000}(5)$

当E_r/1 000 < 2.6时, 将式(5)中的E_r/1 000用2.6代替, 计算得到F_Adj。另外, 根据式(4)计算出的β还要乘以0.7的修正系数。

对Ayres模型进行的研究表明, 它也存在一定缺陷, 如预测的车辙量高度分散与过高等。AASHTO 2002设计指南仍然采用式(2)的塑性应变和弹性应变关系式, 但利用大量的试验数据对系数回归公式进行了改进^[13], 结果如下

$\{\begin{array}{l}\lg \left(\frac{\epsilon {}_0}{\epsilon {}_{\text{r}}}\right)=\frac{0.15\text{e}{}^{\rho {}^{\beta }}+20\text{e}{}^{\left(\frac{\rho }{10{}^9}\right){}^{\beta }}}{2}\\ \lg (\beta )=-0.61119-0.017638W{}_{\text{c}}\\ \rho =10{}^9\left[\frac{-4.89285}{1-(10{}^9){}^{\beta }}\right]{}^{\frac{1}{\beta }}\end{array}(6)$

国内沥青路面车辙的研究多集中在沥青和沥青混合料的永久变形方面^[15-16], 对于路基土的永久变形研究得较少。邱延峻和孙振堂在对几种路基土进行重复加载试验后, 提出的永久变形预估模型^[3]为

$\begin{array}{l}\epsilon {}_{\text{p}}=\epsilon {}_{\text{p}}^{(1)}f({\rm N})(7)\\ \epsilon {}_{\text{p}}^{(1)}=p{}_{1}r{}_{\sigma }^{p{}_2}(8)\\ f({\rm N})={\rm N}{}^{p{}_3}r{}_{\sigma }^{p{}_4}(9)\end{array}$

式中: ε_p⁽¹⁾为初次轴载作用产生的塑性应变, %;r_σ为应力比(偏应力/强度); f(N)为累积函数; p₁、p₂、p₃和p₄为材料参数。

邱延峻和孙振堂没有给出模型中的材料参数与含水量、干密度或回弹模量等常规参数之间的回归关系, 设计部门在使用该模型时必须要进行重复加载动三轴试验, 因此, 极大地限制了该模型的应用。

由于国内外的路面结构、轴载、土的性质等存在较大差异, 国外的永久变形预估模型是否适合中国还需进行试验验证。在国外提出的众多路基土永久变形预估模型中, Tseng和Lytton提出的塑性应变和弹性应变之间的关系式通过了大量室内试验和试验路的验证, 被AASHTO 2002设计指南采用, 可信度最高, 故本文利用室内永久变形试验重点对该模型进行验证, 必要时进行修正。

2.   砂土重复加载动三轴试验

2.1   砂土基本物理性质

试验用土为取自重庆的砂土, 该土的基本物理性质见表 1。

表  1  土的基本性质

Table  1.  Basic properties of soil

指标	最大干密度DMD/(g·cm-3)	最佳含水量/%	相对密度	液限/%	塑限/%	塑性指数
测定值	2.00	11.1	2.658	20.64	16.09	10.55

下载: 导出CSV 

| 显示表格

2.2   试验方案

目前国内外均没有测试路基土永久变形的标准试验方案, 但美国T307-99、LTPP P46-96、NCHRP 1-28和NCHRP 1-28A等规范中给出了测试路基土回弹模量的标准试验方案。本文参考路基土回弹模量的试验方案和中国对于路基土压实度、含水量等的规定, 在UTM试验机上对砂土进行重复加载动三轴试验。试验方案如下: 试件直径为100 mm, 高度为200 mm, 经压实成型, 压实度K分别取91%和96%, 含水量分别取最佳含水量的105%、110%和120%, 平行试件取3个; 荷载型式为半正弦, 频率为1 Hz, 加载时间为0.2 s, 间歇时间为0.8 s, 作用次数取10 000次; 围压取28 kPa, 偏应力分别取28、48和69 kPa。

2.3   试验结果

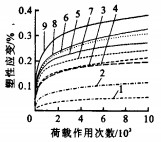
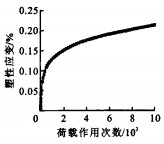
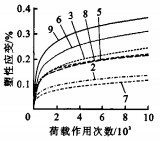
当偏应力比较小(为28 kPa)时, 部分工况下试件的累积永久变形先增后降, 最后再增, 明显不符合永久变形逐渐增长的基本规律, 因此, 剔除此类试验结果。另外, 由于压头与试件之间的挤密等原因, 大部分工况下前10~20次加载产生的永久变形占总永久变形的比例过大(有时第1次加载产生的永久变形占总永久变形的50%以上), 明显与事实不符; 同时, 在路面施工时压路机还将继续对路基进行后续压实, 相当于室内试验前10~20次加载, 路基后续压实对于公路运营过程中的路表车辙没有贡献, 因此, 可以认为室内试验前10~20次加载对于路表车辙没有贡献。鉴于以上原因, 从第21次加载开始计算永久变形。试验得到的砂土的永久变形曲线见图 1、2, 图中工况1代表105-28(即含水量为最佳含水量的105%, 围压为28 kPa, 其他工况中各符号的含义与之类似); 2代表105-48;3代表105-69;4代表110-28;5代表110-48;6代表110-69;7代表120-28;8代表120-48;9代表120-69。

图  1  K为91%时的永久变形

Figure  1.  Permanent deformations when K=91%

下载: 全尺寸图片 幻灯片

图  2  K为96%时的永久变形

Figure  2.  Permanent deformations when K=96%

下载: 全尺寸图片 幻灯片

3.   砂土永久变形预估模型

3.1   永久变形预估模型的建立

采用最小二乘法, 根据式(2), 对试验曲线进行拟合, 可得到回弹模量、相关系数以及lg(ε₀/ε_r)、lg(ρ)、lg(β)见表 2, 可以看出, 相关系数R²很高, 均在0.99以上。图 3中给出工况96-105-69(即压实度为96%, 含水量为最佳含水量的105%, 围压为69 kPa, 表 2中其余各工况的含义与之类似)的拟合曲线, 可以看出, 拟合曲线和试验结果吻合得非常理想。

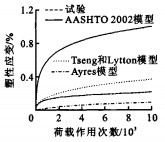
表  2  永久变形曲线拟合结果

Table  2.  Fitting result of permanent deformation curve

工况	回弹应变εr	回弹模量/MPa	R2	lg(ε0/εr)	lg(ρ)	lg(β)
91-105-48	0.001 25	38.40	0.998 7	0.702 430 536	5.439 378	-0.882 56
91-105-69	0.001 85	37.30	0.999 6	0.664 794 386	4.583 399	-0.769 70
91-110-48	0.001 55	30.97	0.998 0	0.690 481 894	4.612 529	-0.816 25
91-110-69	0.001 75	39.43	0.998 5	0.902 779 666	5.240 023	-0.851 34
91-120-48	0.001 60	30.00	0.998 7	0.426 307 892	3.258 652	-0.642 92
91-120-69	0.001 95	35.38	0.999 5	0.561 834 989	3.236 714	-0.635 37
96-105-28	0.000 60	46.67	0.999 5	0.758 407 192	6.594 742	-0.807 80
96-105-48	0.001 05	45.71	0.999 7	0.492 028 301	4.116 664	-0.722 60
96-105-69	0.001 40	49.29	0.998 9	0.566 521 666	3.750 246	-0.719 47
96-110-28	0.000 65	43.08	0.999 8	0.629 566 412	2.521 400	-0.509 38
96-110-48	0.001 20	40.00	0.999 7	0.573 065 095	2.815 113	-0.600 05
96-110-69	0.001 85	37.30	0.999 5	0.540 363 300	3.387 230	-0.684 79
96-120-28	0.001 00	28.00	0.998 6	0.597 695 186	2.760 121	-0.619 28
96-120-48	0.001 75	27.43	0.998 4	0.520 389 945	2.690 905	-0.593 07
96-120-69	0.002 15	32.09	0.999 3	0.508 921 011	3.037 904	-0.643 40

下载: 导出CSV 

| 显示表格

图  3  永久变形拟合曲线

Figure  3.  Fitting curve of permanent deformation

下载: 全尺寸图片 幻灯片

对于工况96-105-69, 永久变形试验结果和Tseng和Lytton模型、Ayres模型、AASHTO 2002模型的计算结果对比见图 4, 可以看出, 试验曲线和各理论曲线形式比较接近, 但数值差别较大。当荷载作用次数为10 000次时, 根据AASHTO 2002模型、Tseng和Lytton模型以及Ayres模型计算出的结果和试验结果相对误差分别为376%、71%和52%, 说明各理论模型均不能适于试验用砂土。表 2、图 3、4表明, 砂土塑性应变和荷载作用次数关系式可以采用式(2), 但公式中的系数需要根据试验结果重新确定。

图  4  试验与理论结果对比

Figure  4.  Comparison of test result and calculation results

下载: 全尺寸图片 幻灯片

根据试验结果重新回归, 得到各系数与含水量和回弹模量的相关关系式为

$\{\begin{array}{cc}\lg \left(\frac{\epsilon {}_0}{\epsilon {}_{\text{r}}}\right)=2.18784-0.11229W{}_{\text{c}}-0.005427E{}_{\text{r}}\hfill & (R{}^2=0.37)\hfill \\ \lg (\rho )=23.18288-1.41508W{}_{\text{c}}-0.04981E{}_{\text{r}}\hfill & (R{}^2=0.46)\hfill \\ \lg (\beta )=-3.03719+0.15938W{}_{\text{c}}+0.009936E{}_{\text{r}}\hfill & (R{}^2=0.54)\hfill \end{array}(10)$

同样可以得到各系数和含水量的回归关系式为

$\{\begin{array}{l}\lg \left(\frac{\epsilon {}_0}{\epsilon {}_{\text{r}}}\right)=1.4729-0.071W{}_{\text{c}}(R{}^2=0.42)\\ \lg (\rho )=16.621-1.036W{}_{\text{c}}(R{}^2=0.37)\\ \lg (\beta )=-1.7282+0.0838W{}_{\text{c}}(R{}^2=0.31)\end{array}(11)$

3.2   永久变形预估模型的可靠性分析

本试验有效工况为14个, 取显著性水平α为0.05, 根据数理统计原理可以查得相关系数临界值R_α为0.532, 则R_α²为0.28。lg(ε₀/ε_r)、lg(ρ)、lg(β)与含水量和回弹模量的相关系数均大于R_α², 与含水量的相关系数也均大于R_α², 故对于砂土, 塑性应变和荷载作用次数之间的关系式仍然采用式(2), 可根据式(10)或式(11)确定各系数。

鉴于试验样本数不是很大, 而且限于条件尚未经过试验路验证, 使用本文建立的永久变形预估模型时宜满足4个条件: 土类为砂土; 压实度为91%~96%;含水量为最佳含水量的105%~120%;在路基工作区内围压接近28 kPa, 竖向压应力为28~69 kPa。

4.   结语

(1) Tseng和Lytton提出的塑性应变和荷载作用次数之间的关系式可以用于预估砂土的永久变形, 但Tseng和Lytton模型、Ayres模型和AASHTO 2002模型中的系数与含水量或回弹模量之间的回归关系式不适用于砂土。

(2) 根据Tseng和Lytton提出的塑性应变和荷载作用次数之间的关系式以及本文建立的该公式中的系数与含水量和回弹模量以及其与含水量之间的回归公式, 可建立砂土永久变形预估模型, 并可将其用于中国沥青路面车辙预估。

(3) 将来可以增加重复加载试验的荷载作用次数(如增加到10万次, 甚至100万次以上)研究砂土的永久变形特性, 并将建立的永久变形预估模型通过试验路观测进行验证。