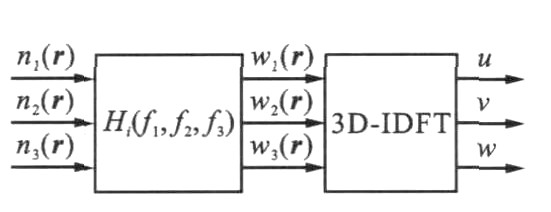
-
摘要: 为了提高飞机穿越大气紊流场时的实时飞行仿真逼真度, 提出了三维空间大气紊流场的生成与扩展方法。采用Von Karman模型, 在频域空间直接进行蒙特卡罗法随机抽样, 经三维傅立叶逆变换得到三维空间大气紊流场。基于傅立叶变换的复共轭对称特性, 生成实的紊流场。在飞行仿真过程中, 对预先生成的无因次紊流场进行有因次化, 保证紊流场尺度和强度随飞行高度动态变化。运用基于对称扩展的紊流场扩展方法, 保证生成的局部空间紊流场有效扩展为大范围连续紊流场。仿真结果表明: 生成的三维紊流场在对称扩展前、后均符合Von Karman模型, 且与基于紊流场相关函数矩阵的生成方法相比, 新算法计算速度快, 存储空间需求少, 更适于实时飞行仿真。Abstract: In order to improve the real-time flight simulation fidelity of aircraft through turbulence field, the generation and extension methods of 3D atmospheric turbulence field were put forward.Based on Von Karman model, spatial turbulence field was generated in frequency domain by using Monte Carlo method and transformed back to time domain by using 3D Fourier inverse transform.The conjugate characteristic of Fourier transform was applied to guarantee the realism of turbulence field in time domain.During flight simulation, the integral scale and intensity of turbulence field changed with flight altitude by dimensioning the non-dimensional turbulence field which had been generated in advance.A symmetrical turbulence extension method was presented to make sure that the local field could be effectively extended to wide range and continuous field.Simulation result indicates that turbulence field conforms to Von Karman model before and after symmetrical extension, compared to the generation method based on correlation function matrix, the new algorithms have faster generation speed and less storage space, so they are suitable for real-time flight simulation.
-
表 1 傅立叶变换的复共轭对称关系
Table 1. Conjugate relations in Fourier transform
一维对称性 X(M-k)=X*(k), Im X(M/2)=0 二维对称性 X(M1-k1, 0)=X*(k1, 0), Im X(M1/2, 0)=0 X(0, M2-k2)=X*(0, k2),
Im X(0, M2/2)=0X(M1-k1, M2-k2)=X*(k1, k2),
Im X(M1/2, M2/2)=0三维对称性 X(M1-k1, 0, 0)=X*(k1, 0, 0),
Im X(M1/2, 0, 0)=0X(0, M2-k2, 0)=X*(0, k2, 0),
Im X(0, M2/2, 0)=0X(0, 0, M3-k3)=X*(0, 0, k3),
Im X(0, 0, M3/2)=0X(M1-k1, M2-k2, 0)=X*(k1, k2, 0),
Im X(M1/2, M2/2, 0)=0X(M1-k1, 0, M3-k3)=X*(k1, 0, k3),
Im X(M1/2, 0, M2/2)=0X(0, M2-k2, M3-k3)=X*(0, k2, k3),
Im X(0, M2/2, M3/2)=0X(M1-k1, M2-k2, M3-k3)=X*(k1, k1, k3),
Im X(M1/2, M2/2, M3/2)=0
下载: 导出CSV
-
[1] ETKI N B. Turbulent wind and its effect on flight[J]. Journal of Aircraft, 1981, 18(5): 327-345. doi: 10.2514/3.57498 [2] 肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993. [3] ROBI NSON P A, REID L D. Modeling of turbulence and down bursts for flight simulators[J]. Journal of Aircraft, 1990, 27(8): 700-707. doi: 10.2514/3.25343 [4] 赵震炎, 肖业伦, 施毅坚. Dryden大气紊流模型的数字仿真技术[J]. 航空学报, 1986, 7(5): 433-443. doi: 10.3321/j.issn:1000-6893.1986.05.003ZHAO Zhen-yan, XIAO Ye-lun, SHI Yi-jian. Adigital simulation technique for Dryden atmospheric turbulence model[J]. Acta Aeronautica et Astronautica Sinica, 1986, 7(5): 433-443. (in Chinese) doi: 10.3321/j.issn:1000-6893.1986.05.003 [5] 洪冠新, 肖业伦. 用蒙特卡罗法仿真生成三维空间大气紊流场[J]. 航空学报, 2001, 22(6): 542-545. doi: 10.3321/j.issn:1000-6893.2001.06.010HONG Guan-xin, XI AO Ye-lun. Monte Carlo simulation for 3-D-field of at mospheric turbulence[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(6): 542-545. (in Chinese) doi: 10.3321/j.issn:1000-6893.2001.06.010 [6] 肖业伦. 用于飞行仿真的二维紊流场的数字生成法[J]. 航空学报, 1990, 11(4): B124-B130. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB199004001.htmXI AO Ye-lun. Digital generation of two-dimensional field of turbulence for flight simulation[J]. Acta Aeronautica et Astronautica Sinica, 1990, 11(4): B124-B130. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB199004001.htm [7] 陆宇平, 胡亚海. 基于空间相关函数的二维紊流场数值生成法[J]. 南京航空航天大学学报, 1999, 31(2): 139-145. doi: 10.3969/j.issn.1005-2615.1999.02.004LU Yu-ping, HU Ya-hai. Digital generation of two-dimensional field of turbulence based on spatial correlation function[J]. Journal of Nanjing University of Aeronautics and Astronautics, 1999, 31(2): 139-145. (in Chinese) doi: 10.3969/j.issn.1005-2615.1999.02.004 [8] TATOMF B, SMITHS R, FICHTL G H, et al. Si mulationof at mospheric turbulent gusts and gust gradients[J]. Journal of Aircraft, 1982, 19(4): 264-271. doi: 10.2514/3.57388 [9] CAMPBELL C W, SANBORN V A. Aspatial model of windshear and turbulence[J]. Journal of Aircraft, 1984, 21(12): 929-935. doi: 10.2514/3.45065 [10] 刘培森. 应用傅立叶变换[M]. 北京: 北京理工大学出版社, 1991. -
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 361
- HTML全文浏览量: 87
- PDF下载量: 1464
- 被引次数: 0
