Approximate mean value analysis method of maintenance ability for civil aeroengine maintenance workshop
-
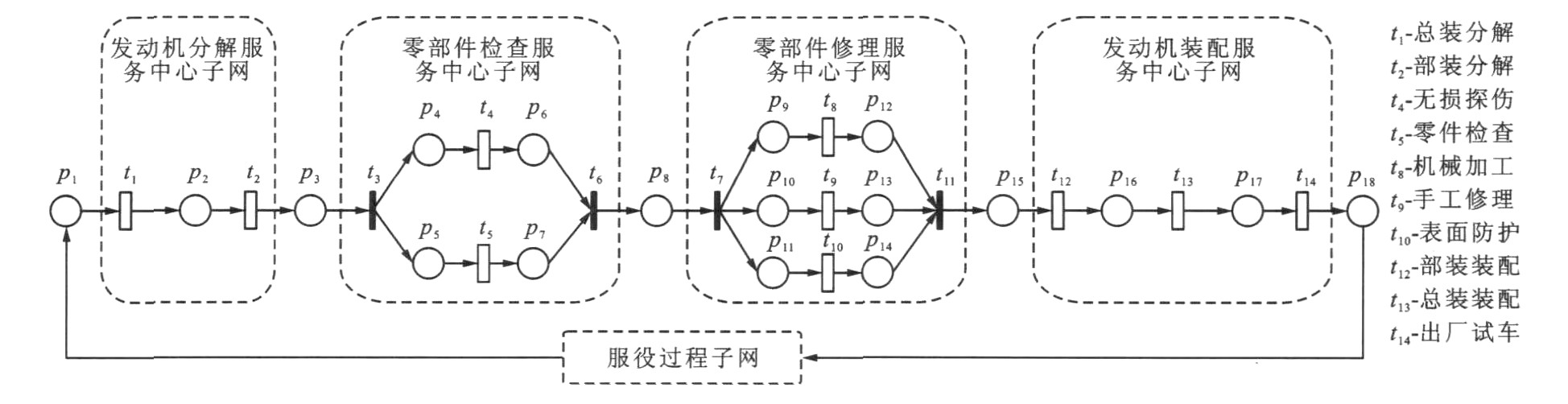
摘要: 为了评估民航发动机维修车间在当前维修能力下可保持的机队规模, 提出了车间维修能力近似平均值分析方法。采用扩展随机Petri网建立了发动机在维修车间的转移模型, 利用单维修等级下系统的性能指标对多维修等级性能指标进行了修正, 采用平方变差系数方法实现服务时间从指数分布向正态分布的逼近, 并评价了多等级与服务时间为正态分布的车间维修能力, 分析了近似平均分析法与仿真方法的计算结果。比较结果表明: 各维修中心等待队长最大相对误差为9.14%, 此时零件检查、手工修理及机械加工为限制维修车间能力的瓶颈, 因此, 近似平均值分析方法是有效的。
-
关键词:
- 民航发动机 /
- 车间维修能力 /
- 近似平均值分析 /
- 扩展随机Petri网
Abstract: To evaluate the scale of aeroengines fleet under the available maintenance capacity of civil aeroengine maintenance workshop, an approximate mean value analysis method of the maintenance ability was proposed.The transferring model of aeroengine in the workshop was built by using extended stochastic Petri net, multi-level maintenance service performance indexes were revised by using single level performance indexes, squared variation coefficient method was used to approximate service time with normal distribution, and the evaluation results of the ability by using approximate mean value analysis method and simulation method were compared.The result indicates that the maximal relative error of queuing length for maintenance sections is 9.14%, part checking, handcrafted repairing and mechanical machining are the bottlenecks of the workshop performance, so the method is proved to be efficient. -
图 1 航空发动机维修过程扩展随机Petri网
Figure 1. Extended stochastic Petri net of aeroengine maintenance procedure
表 1 维修工段消耗工时分布参数
Table 1. Distribution parameters of spending times for maintenance sections
关键工段 总装分解 部装分解 无损探伤 零件检查 机械加工 手工修理 表面防护 部装装配 总装装配 出厂试车 期望μPOHi 3.85 5.55 8.84 22.55 15.65 32.87 8.45 6.45 4.65 3.35 方差σPOHi 1.22 2.55 3.65 10.43 6.43 12.54 2.54 1.43 1.35 0.94 期望μOHi 4.75 6.25 10.94 28.65 18.75 44.75 14.75 8.55 5.42 4.15 方差σOHi 2.43 2.86 4.67 13.65 8.43 15.63 4.54 2.13 2.04 1.18 
下载: 导出CSV
表 2 结果比较
Table 2. Comparison of results
库所 性能恢复 大修 Np(k) N′p(k) Ep(k) Np(k) N′p(k) Ep(k) P1 0.499 42 0.516 20 3.360 0.699 10 0.637 25 8.847 P2 0.785 75 0.713 90 9.144 0.972 85 1.033 75 6.260 P3 0.000 00 0.012 15 — 0.000 00 0.004 35 — P4 1.276 00 1.162 25 8.914 1.392 50 1.292 15 7.206 P5 2.839 50 2.662 15 6.245 4.081 20 4.273 95 4.723 P6 1.596 55 1.621 75 1.578 2.688 70 2.608 90 2.968 P7 0.033 03 0.031 75 3.887 0.000 00 0.007 15 — P8 0.000 00 0.018 80 — 0.000 00 0.004 65 — P9 2.302 35 2.149 35 6.645 2.582 80 2.733 90 5.850 P10 4.308 75 3.988 25 7.438 6.207 55 5.988 00 3.536 P11 1.137 40 1.238 20 8.862 2.076 80 1.953 20 5.951 P12 2.034 75 1.938 25 4.742 3.647 95 3.718 85 1.943 P13 0.028 10 0.026 45 5.871 0.023 23 0.022 75 2.051 P14 3.199 70 2.948 80 7.841 4.153 95 4.271 70 2.834 P15 0.829 90 0.899 30 8.362 1.034 15 0.993 65 3.916 P16 0.564 85 0.565 40 0.097 0.786 70 0.801 70 1.907 P17 0.458 59 0.469 90 2.466 0.569 65 0.575 65 1.053 P18 50.151 80 50.935 00 1.561 46.125 65 45.512 50 1.329
下载: 导出CSV
-
[1] GATLAND R, YANG E, BUXTON K. Solving enginemaintenance capacity problems with simulation[C]//Georgia Institute of Technology. Proceedings of the 29th Conferenceon Winter Si mulation. Washington DC: IEEE Computer Society, 1997: 892-899. [2] BAZARGAN M, MCGRATH R N. Discrete event simulation to improve aircraft availability and maintainability[C]//Tampa Florida. 2003 Proceedings of Annual Reliability and Maintainability Symposium. New Jersey: IEEE Operation Center, 2003: 63-67. [3] 汪自勤, 宋文忠, 冯纯伯. 离散事件动态系统的分析和优化——排队网络模型方法(上)[J]. 信息与控制, 1989, 18(6): 31-44. https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK198906006.htmWANG Zi-qin, SONG Wen-zhong, FENG Chun-bo. Analysis and optimization of DEDS(discrete event dynamic systems)—queueing network model method[J]. Information and Control, 1989, 18(6): 31-44. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK198906006.htm [4] 左洪福, 张海军, 戎翔. 基于比例风险模型的航空发动机视情维修决策[J]. 航空动力学报, 2006, 21(4): 716-721. doi: 10.3969/j.issn.1000-8055.2006.04.018ZUO Hong-fu, ZHANG Hai-jun, RONG Xiang. Conditionbased aero-engine maintenance decision method using proportional hazards model[J]. Journal of Aerospace Power, 2006, 21(4): 716-721. (in Chinese) doi: 10.3969/j.issn.1000-8055.2006.04.018 [5] 吕敬堂. 排队论在油泵修理中的应用[J]. 系统工程理论与实践, 2000, 20(6): 83-90. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL200006014.htmLU Jing-tang. Application of queuing theory in fuel pumprepair[J]. Systems Engineering-Theory and Practice, 2000, 20(6): 83-90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL200006014.htm [6] 刘坚, 于德介, 李蓉, 等. 基于广义随机Petri网的维护系统仿真与应用[J]. 机械工程学报, 2005, 41(10): 164-169. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200510034.htmLI UJian, YU De-jie, LI Rong, et al. Research on general stochastic Petri net based maintenance system simulation and optimization[J]. Chinese Journal of Mechanical Engineering, 2005, 41(10): 164-169. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200510034.htm [7] HENDERSON W, TAYLOR P G. Embedded processes instochastic Petri nets[J]. IEEE Transactions on Software Engineering, 1991, 17(2): 108-116. doi: 10.1109/32.67592 [8] SERENO M, BALBO G. Mean value analysis of stochastic Petrinets[J]. Performance Evaluation, 1997, 29(1): 35-62. [9] BALBO G, BRUELL S C, SERENO M. Arrival theorems for product—form stochastic Petri nets[C]//ACM. Proceedings ofthe 1994 ACM SIGMETRICS Conference on Measurement and Modeling of Computer Systems. New York: ACM, 1994: 87-97. [10] SERENO M. Approxi mate mean value analysis technique fornon-product form solution stochastic Petri nets: an application to stochastic marked graphs[C]//Duke University. Proceedings of the 16th International Workshop on Petri Netsand Performance Models. Washington DC: IEEE Computer Society, 1995: 42-51. -
点击查看大图
图(2) / 表(2)
计量
- 文章访问数: 274
- HTML全文浏览量: 90
- PDF下载量: 497
- 被引次数: 0
