Modelling method for reliability of traction power supply system
Article Text (Baidu Translation)
-
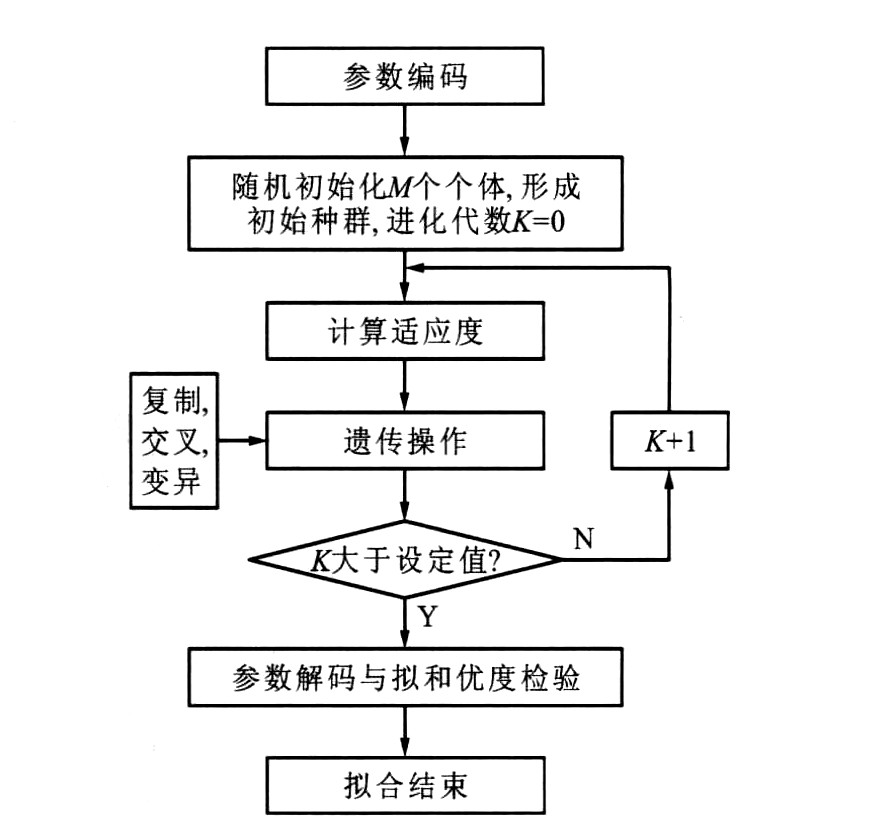
摘要: 采用基于遗传算法的拟合方法, 提出了一种以威布尔分布模型为基础的牵引供电系统的可靠性建模方法。以京广线郑州南段牵引供电系统为例, 根据统计的14年设备失效率信息, 采用建模方法建立了牵引供电系统各设备的可靠性模型, 运用BDD算法得到整个牵引供电系统的可靠性模型, 计算了系统的有效寿命。拟合优度的K-S和W2检验结果表明: 该建模方法是一种适用于牵引供电系统特别是接触网系统可靠性分析的。有效寿命的计算结果表明: 牵引供电系统与接触网的有效寿命分别为3.116年与3.215年, 供电系统的可靠性在很大程度上取决于接触网的可靠性。Abstract: Using a fitting method based on genetic algorithm (GA), a reliability modelling method of traction power supply system based on Weibull distribution model was proposed.Southern Zhengzhou traction power supply system (TPSS) on Jing-Guang railway was taken an example, its real failure ratio data for 14 years were analyzed, the reliability models of all components of the system were established by the method, based on these, the reliability model of whole system was analyzed by using binary decision diagram (BDD) algorithm, and the life-span of the system was calculated.K-S and W2 goodness-of-fit test result shows that the modeling method is feasible.The computation result of the life-span indicates that the life-span of the system is 3.116 years, the life-span of catenary system is 3.215 years, the reliability of the system depends on the reliability of catenary system to large extent.
-
Key words:
- TPSS /
- reliability /
- GA /
- BDD algorithm /
- Weibull distribution
-
图 2 牵引变电所主接线简图
Figure 2. Simplified main wiring diagram of traction power supply substation
表 1 故障率的实测数据
Table 1. Factual data of failure ratios
时间/年 牵引变压器 隔离开关 电流互感器 接触导线 承力索 绝缘子 1 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 2 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 3 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 4 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 5 0.000 000 0.000 000 0.000 000 0.000 461 0.000 000 0.001 955 6 0.000 000 0.000 000 0.000 000 0.001 797 0.000 000 0.000 000 7 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 062 8 0.000 000 0.000 000 0.000 000 0.007 208 0.000 000 0.000 000 9 0.000 000 0.015 766 0.000 000 0.019 314 0.001 787 0.000 000 10 0.000 000 0.000 000 0.000 000 0.018 493 0.000 000 0.000 105 11 0.000 000 0.000 000 0.000 000 0.008 301 0.000 000 0.000 000 12 0.004 167 0.000 000 0.000 000 0.016 731 0.000 000 0.000 000 13 0.000 000 0.000 000 0.000 000 0.031 731 0.000 498 0.000 000 14 0.083 330 0.083 330 0.083 330 0.083 333 0.083 333 0.083 333 
下载: 导出CSV
表 2 故障率拟合结果
Table 2. Fitting result of failure ratios
时间/年 牵引变压器 隔离开关 电流互感器 接触导线 承力索 绝缘子 1 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 2 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 3 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 4 0.000 001 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 5 0.000 003 0.000 000 0.000 000 0.000 000 0.000 000 0.000 000 6 0.000 010 0.000 003 0.000 000 0.000 000 0.000 001 0.000 000 7 0.000 031 0.000 017 0.000 000 0.000 000 0.000 006 0.000 000 8 0.000 081 0.000 069 0.000 000 0.000 000 0.000 035 0.000 000 9 0.000 188 0.000 241 0.000 000 0.000 000 0.000 172 0.000 004 10 0.000 397 0.000 737 0.000 000 0.000 000 0.000 712 0.000 046 11 0.000 782 0.002 024 0.000 000 0.000 008 0.002 580 0.000 406 12 0.001 452 0.005 090 0.000 000 0.000 166 0.008 357 0.002 975 13 0.002 566 0.011 893 0.000 016 0.002 605 0.024 638 0.018 573 14 0.004 347 0.026 091 0.110 310 0.033 248 0.067 044 0.101 210
下载: 导出CSV
表 3 可靠性模型的参数与检验结果
Table 3. Parameters of reliability models and test results
设备名称 拟合参数 K-S检验(a=0.01) W2检验(a=0.01) α β D 接受否 W2 接受否 电流互感器 170.629 120.656 1.000 否 0.710 是 隔离开关 182.703 11.602 0.867 是 0.470 是 牵引变压器 226.043 8.113 0.952 是 0.813 否 接触导线 177.000 35.363 0.989 否 0.700 是 承力索 170.957 14.508 0.849 是 0.247 是 绝缘子 170.406 23.879 0.911 是 0.229 是
下载: 导出CSV
表 4 牵引变电所主要设备
Table 4. Main equipments of traction power supply substation
设备种类 符号 电流互感器 CTi (i=1, 2, …, 8) 断路器 DLi (i=1, 2, …, 8) 自动隔离开关 GLi (i=1, 2, …, 8) 牵引变压器 Ti (i=1, 2)
下载: 导出CSV
表 5 可靠性模型参数与平均寿命
Table 5. Parameters of reliability models and average life-spans
系统 可靠性模型参数 平均寿命/年 α β 牵引变电所 150.87 13.52 11.093 接触网 55.17 4.86 3.215 牵引供电系统 54.21 4.36 3.116
下载: 导出CSV
-
[1] 黄炜. 从绝缘子的应用探讨提高接触网可靠性的措施[J]. 电气化铁道, 2005, 16 (3): 8-10. https://www.cnki.com.cn/Article/CJFDTOTAL-DQHD200503003.htmHUANG Wei. Discussion on measures for improving OCS' reliability based on insulator s application[J]. Electric Railway, 2005, 16 (3): 8-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQHD200503003.htm [2] 万毅, 邓斌, 李会杰, 等. 基于FTA的接触网系统可靠性研究[J]. 铁道工程学报, 2005, 22 (6): 55-59. doi: 10.3969/j.issn.1006-2106.2005.06.015WAN Yi, DENG Bin, LI Hui-jie, et al. Research on reliability of the catenary systembased on FTA[J]. Journal of Railway Engineering Society, 2005, 22 (6): 55-59. (in Chinese) doi: 10.3969/j.issn.1006-2106.2005.06.015 [3] 万毅, 邓斌, 柯坚, 等. 基于神经网络RBF的接触网可靠性分析[J]. 铁道学报, 2005, 27 (6): 39-42. doi: 10.3321/j.issn:1001-8360.2005.06.007WAN Yi, DENGBin, KEJian, et al. Reliability analysis of catenary systems based on neural networks RBF[J]. Journal of the China Railway Society, 2005, 27 (6): 39-42. (in Chinese) doi: 10.3321/j.issn:1001-8360.2005.06.007 [4] 张卫东, 贺威俊. 电力牵引接触网系统可靠性模型研究[J]. 铁道学报, 1993, 15 (1): 31-38. doi: 10.3321/j.issn:1001-8360.1993.01.005ZHANG Wei-dong, HE Wei-jun. Research on reliability modelling of electrical tractioncatenary system[J]. Journal of the China Railway Society, 1993, 15 (1): 31-38. (in Chinese) doi: 10.3321/j.issn:1001-8360.1993.01.005 [5] 刘凤, 李群湛. 引入事例推理的牵引变电所故障分析专家系统[J]. 继电器, 2006, 34 (10): 77-80. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW200610018.htmLI U Feng, LI Qun-zhan. Fault analysis expert system of transformer substation based on case-based reasoning[J]. Relay, 2006, 34 (10): 77-80. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW200610018.htm [6] 陈绍宽. 铁道牵引供电系统维修计划优化模型与算法[D]. 北京: 北京交通大学, 2006. [7] 刘金琨. 智能控制[M]. 北京: 电子工业出版社, 2005. [8] FERDOUS J, BORHAN U M, PANDEY M. Reliability esti mation with Weibull inter failure times[J]. Reliability Engineering and SystemSafety, 1995, 50 (3): 285-296. https://www.sciencedirect.com/science/article/pii/0951832095000860 [9] 冯振宇, 诸德培. 威布尔分布的拟合优度检验[J]. 机械强度, 1996, 18 (4): 28-31. https://www.cnki.com.cn/Article/CJFDTOTAL-JXQD604.007.htmFENG Zhen-yu, ZHU De-pei. Modified goodness-of-fit tests for Weibull distribution[J]. Journal of Mechanical Strength, 1996, 18 (4): 28-31. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXQD604.007.htm [10] 方开泰, 许建伦. 统计分布[M]. 北京: 科学出版社, 1987. [11] 史定华, 王松瑞. 故障树分析技术方法和理论[M]. 北京: 北京师范大学出版社, 1993. [12] JUNG WS, HAN S H, HA J. Afast BDD algorithm for large coherent fault trees analysis[J]. Reliability Engineering and SystemSafety, 2004, 83 (3): 369-374. https://www.sciencedirect.com/science/article/pii/S0951832003002369 [13] RAUZY A. New algorithms for fault trees analysis[J]. Reliability Engineering and System Safety, 1993, 40 (3): 203-211. doi: 10.1007/978-3-319-69096-4_80 -
点击查看大图
图(3) / 表(5)
计量
- 文章访问数: 446
- HTML全文浏览量: 146
- PDF下载量: 193
- 被引次数: 0
