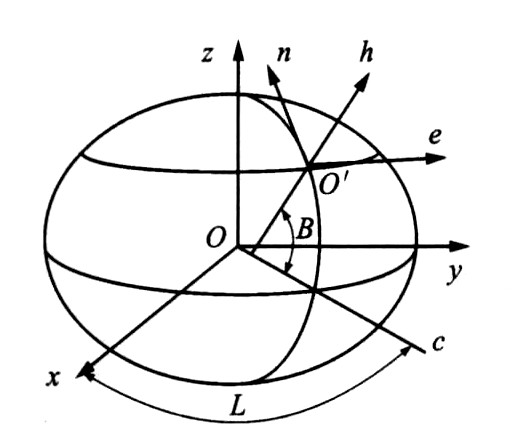
-
摘要: 研究并推导了以地平坐标系为参考坐标系的GPS公路滑坡监测网数据处理模型, 提出了应用聚类分析方法对拟稳点(或固定基准点)的相对稳定性进行检验的数学模型, 采用拟稳平差法进行平差计算。在VC++环境下, 开发了GPS公路滑坡监测网的数据处理软件系统, 以此对某公路滑坡GPS变形监测网的3期观测数据进行平差计算。平差计算结果表明: GPS公路滑坡监测网的平面坐标中误差可以达到1 mm, 垂直坐标可以达到2 mm, 因此, 提出的数学模型适合于GPS公路滑坡变形监测网的数据处理。Abstract: The data processing model based on station orthogonal coordinate system for 3D GPS highway subsidence monitoring network was analyzed and derived, a mathematical model based on clustering analysis method was put forward to test the relative stability of quasistable points(or datum points), and a quasistable adjustment method in the data processing course was proposed to compute minitoring data adjustments.A software system of data processing for the network was developed by using VC++, and the adjustments of three periods observation data of a highway subsidence from the network were computed by using the software.Calculation result shows that the middle square error of the plane coordinate is 1 mm, and the plumb one is 2 mm, so the mathematical model is more suitable for the data processing in the network.
-
表 1 显著水平α与临界值λ的对应值
Table 1. Corresponding values between significant levelαand critical valueλ
α/% 6.00 2.00 0.33 0.20 λ 0.138 5 0.041 6 0.010 8 0.003 6 
下载: 导出CSV
表 2 基线精度
Table 2. Precisions of base lines
mm 观测期数 Δn基线 Δe基线 Δh基线 平均中误差 最大中误差 平均中误差 最大中误差 平均中误差 最大中误差 第1期 0.85 1.79 0.97 1.89 1.68 3.25 第2期 0.77 1.81 0.87 1.89 1.36 2.69 第3期 0.65 1.63 0.75 1.69 1.31 2.28
下载: 导出CSV
表 3 三维坐标综合精度
Table 3. General precisions of 3D coordinates
mm 观测期数 n坐标 e坐标 h坐标 平均中误差 最大中误差 平均中误差 最大中误差 平均中误差 最大中误差 第1期 0.71 1.05 0.59 0.89 1.31 1.96 第2期 0.59 1.21 0.58 0.92 1.34 2.25 第3期 0.41 0.65 0.53 0.76 0.98 1.53
下载: 导出CSV
-
[1] 李红卫. 山区公路滑坡研究[D]. 西安: 长安大学, 2005. [2] 李征航, 刘志赵, 王泽民. 利用GPS定位技术进行大坝变形观测的研究[J]. 武汉水利电力大学学报, 1996, 29(6): 26-29. https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD606.005.htmLi Zheng-hang, Liu Zhi-zhao, Wang Ze-min. Study on monitoring damdeformation with GPS positioning[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1996, 29(6): 26-29. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD606.005.htm [3] 华锡生, 何秀凤. GPS技术在水电工程中的应用及展望[J]. 水电自动化与大坝监测, 2002, 26(4): 6-9. https://www.cnki.com.cn/Article/CJFDTOTAL-DBGC200204002.htmHua Xi-sheng, He Xiu-feng. Prospect and application of GPS to water conservancy project[J]. Hydropower Automationand Dam Monitoring, 2002, 29(6): 6-9. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBGC200204002.htm [4] 宋迎春. 利用GPS进行边坡滑坡监测的数学模型[J]. 湘潭大学自然科学学报, 2006, 28(1): 105-111. https://www.cnki.com.cn/Article/CJFDTOTAL-XYDZ200601023.htmSong Ying-chun. Mathematical model on landslide monitoring through GPS[J]. Natural Science Journal of Xiangtan University, 2006, 28(1): 105-111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XYDZ200601023.htm [5] 兰孝奇, 岳东杰. 三峡坝区变形监测网多目标优化研究[J]. 河海大学学报: 自然科学版, 2000, 28(1): 82-85. https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX200001016.htmLan Xiao-qi, Yue Dong-jie. Multiobjective opti mization designfor the Three Gorges dam monitoring network[J]. Journal ofHohai University: Natural Sciences, 2000, 28(1): 82-85. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX200001016.htm [6] 刘大杰, 施一民, 过静君. 全球定位系统(GPS)的原理与数据处理[M]. 上海: 同济大学出版社, 1996. [7] 段虎荣, 郭新成, 丁宁. 最小二乘预估法在GPS高程转换中的应用[J]. 西安科技大学学报, 2006, 26(1): 62-69. https://www.cnki.com.cn/Article/CJFDTOTAL-XKXB200601016.htmDuan Hu-rong, Guo Xin-cheng, DING Ning. The least squaresesti mation used in model of GPS altitude transformation[J]. Journal of Xi an University of Science and Technology, 2006, 26(1): 62-69. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XKXB200601016.htm [8] KUANG Shan-long. A strategy for GPS survey planning: choice of opti mumbaselines[J]. Surveying and LandInforma-tion System, 1994, 54(4): 187-201. [9] ZHU Wen-yao, WANG Xiao-ya, CHENG Zong-yi, et al. Crustal motion of Chinese mainland monitored by GPS[J]. Science in China Series D, 2000, 43(4): 394-400. doi: 10.1007/BF02959450 -
点击查看大图
图(1) / 表(3)
计量
- 文章访问数: 206
- HTML全文浏览量: 55
- PDF下载量: 329
- 被引次数: 0
