0.   引言

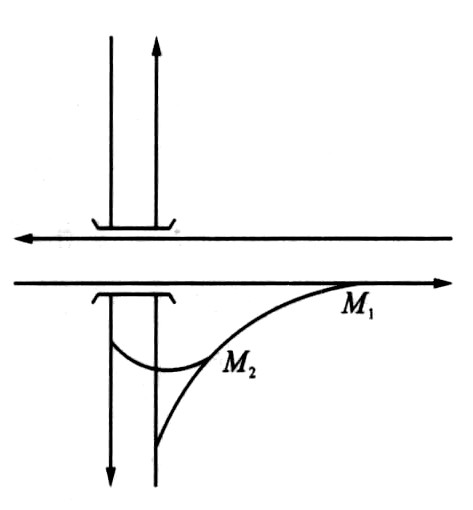
作为匝道布设的一种形式, 对角匝道从交叉线立交前(或后)右(或左)侧分流, 向右(或左)转弯后直接从主线右侧进入主线(图 1)。由于对角匝道具有布线紧凑, 占地较少, 工程费用较少, 线形简单等优点^[1], 其在工程实际中得到了一定的应用。目前虽然关于高速公路匝道的研究较多, 尤其是在匝道控制方面^[2-4], 但国内外关于对角匝道的研究极少。大多数工程实际中采用对角匝道时基本上是从几何线形、用地状况等方面进行考虑, 还没有文献对设置对角匝道的交通量条件进行分析。交通量条件是否满足是对角匝道设置合理与否的主要依据之一, 本文试图从这一方面展开研究, 为互通立交的规划设计提供理论依据。

图  1  对角匝道

Figure  1.  Diagonal ramp

下载: 全尺寸图片 幻灯片

设置对角匝道的交通量条件包括两方面的内容, 首先是对角匝道驶入主线的适应交通量, 记此合流区为合流区1(M₁点); 其次是对角匝道上左转车流的适应交通量, 记此左转车流与右转车流的合流区为合流区2(M₂点)。目前关于合流区1处的交通量研究较多^[5-7], 但研究过程中均假设合流区内主线外车道的车头时距服从同一分布, 然而, 实际研究表明, 合流区内主线外车道的交通量和车头时距分布随着距离合流区鼻端距离的不同而不同^[8-9], 这将直接引起合流区内匝道车辆可汇入主路的交通量的不同, 本文第1节将考虑这种不同对合流区1的对角匝道适应交通量进行研究。目前国内外还未见文献对对角匝道上合流区2处的左转车流适应交通量进行研究, 本文第2节将对该部分内容进行研究。在第1、2节研究的基础上本文得到了设置对角匝道的交通量条件, 即对角匝道驶入主线的适应交通量、驶入对角匝道的左转车流的适应交通量以及驶入对角匝道的左右转交通量的约束条件。

1.   对角匝道驶入主线的适应交通量

1.1   合流区主路外侧1车道交通量模型

对合流区外侧车道的交通量模型, 国外作过大量研究, 目前比较成熟和有代表性的是美国的HCM模型, 但该模型局限于合流区上游。针对这种情况, 国内一些学者开始对合流区内部的交通行为进行研究。李文权等通过对大量调查数据的回归分析提出了合流区内外侧车道不同位置交通量的线性模型^[8]为

$V{}_1(x)=a{}_{1}x+a{}_{2}V{}_{\text{z}}+a{}_{3}V{}_{\text{r}}+a{}_4(1)$

式(1)表明, 合流区内主路外侧车道不同断面的交通量V₁(x)随主线交通量V_z、上匝道交通量V_r、距离合流区鼻端的距离x而变化。其中, 待定系数a₁、a₂、a₃、a₄可通过实地调查进行多元回归确定。

1.2   合流区主路外车道车头时距分布

通过对调查数据的分析处理发现, 合流区内主路外侧车道的车头时距与观测断面的交通量息息相关。当主路外侧车道交通量小于250 veh·h^-1时, 车头时距符合负指数分布(1阶Erlang分布); 当主路外侧车道交通量位于250~500 veh·h^-1时, 车头时距符合2阶Erlang分布; 当主路外侧车道交通量位于500~750 veh·h^-1时, 车头时距符合3阶Erlang分布^[9]。

主路外车道数量相同但车型构成不同的交通流其运行特性有所不同, 对驶入匝道汇入车流的影响也不同, 为了使上述研究结果具有通用性, 按照调查数据的车型比例状况及高速公路合流区主路外车道的车辆换算系数(小型车为1.000, 中型车为1.447, 大型车为1.965)^[10], 将交通量单位换算为pcu·h^-1, 结果为: 当主路外侧车道交通量小于350 pcu·h^-1时, 车头时距符合负指数分布(1阶Erlang分布), 其概率密度函数为

$\begin{array}{l}f(t)=\lambda \text{e}{}^{-\lambda t}(2)\\ \lambda =V{}_1(x)/3600\end{array}$

当主路外侧车道交通量位于350~699 pcu·h^-1时, 车头时距符合2阶Erlang分布, 其概率密度函数为

$\begin{array}{l}f(t)=\lambda {}^{2}t\text{e}{}^{-\lambda t}(3)\\ \lambda =V{}_1(x)/1800\end{array}$

当主路外侧车道交通量位于699~1 049 pcu·h^-1时, 车头时距符合3阶Erlang分布, 其概率密度函数为

$\begin{array}{l}f(t)=\lambda {}^{3}t{}^2\text{e}{}^{-\lambda t}/2(4)\\ \lambda =V{}_1(x)/1200\end{array}$

1.3   对角匝道驶入主路的适应交通量

1.3.1   合流区x处可汇入主路的匝道车辆数

如图 2, 在合流区1, 设主路为单向2车道, 匝道及加速车道为1车道。下面分析距离合流区鼻端x处, 当主路外车道车头时距分别服从负指数分布、2阶Erlang分布及3阶Erlang分布时, 加速车道可汇入的交通量。

图  2  合流区1

Figure  2.  Merging area 1

下载: 全尺寸图片 幻灯片

可接受间隙理论的基本模型形式为^[11]

$c=q{}_{\text{m}}{\displaystyle {\int }_0^{\infty }f}(t)g(t)\text{d}t(5)$

式中: c为次路通行能力; q_m为主路流量; f(t)为主路间隙分布的概率密度函数; g(t)为主路间隙为t时的次路通过量。

记V_m(x)为合流区加速车道x处的可汇入交通量; V₁(x)为合流区主线外侧1车道x处的交通量, f(t, x)为合流区主线外侧1车道x处车头时距分布的概率密度函数, g(t, x)为主线车流间隔为t时加速车道x处能够汇入主线的车辆数, 则

$V{}_{\text{m}}(x)=V{}_1(x){\displaystyle {\int }_0^{\infty }f}(t,x)g(t,x)\text{d}t(6)$

主线车流间隔为t时能够汇入主路的交通量个数有两种表达形式, 一种是离散型, 一种是连续型, 由KYTE^[12]等研究可知用离散型与连续型两种方法计算差别不大, 本文利用连续型表达方式进行求解。连续型表达形式为

$\begin{array}{l}g(t)=\{\begin{array}{cc}0& t<t{}_0\\ \frac{t-t{}_0}{t{}_{\text{f}}}& t\ge t{}_0\end{array}(7)\\ t{}_0=t{}_{\text{c}}-t{}_{\text{f}}/2\end{array}$

式中: t₀为最小可接受间隙; t_c为匝道车辆驶入主路的临界间隙; t_f为匝道车辆连续驶入主路时的随车时距。

当加速车道x处主路外侧车道车头时距分别服从负指数分布、2阶Erlang分布及3阶Erlang分布时, f(t)分别取式(2)~(4), g(t)取式(7), 代入式(6)可得加速车道x处匝道车辆的可汇入交通量V_m1(x)、V_m2(x)、V_m3(x)分别为

$\begin{array}{l}V{}_{\text{m}1}(x)=3600\frac{\text{e}{}^{-V{}_1(x)t{}_0/3600}}{t{}_{\text{f}}}(8)\\ V{}_{\text{m}2}(x)=\frac{\text{e}{}^{-V{}_1(x)t{}_0/1800}}{t{}_{\text{f}}}[V{}_1(x)t{}_0+3600](9)\\ V{}_{\text{m}3}(x)=\frac{V{}_1^2(x)\text{e}{}^{-V{}_1(x)t{}_0/1200}}{2400t{}_{\text{f}}}\cdot \\ \left(t{}_0^2+\frac{4800t{}_0}{V{}_1(x)}+\frac{8640000}{V{}_1^2(x)}\right)(10)\end{array}$

1.3.2   对角匝道驶入主路的适应交通量

如图 2所示, 记高速公路合流区加速车道长度为L, 其中在合流段L₁, 即0~x₁段内主路外侧车道车流车头时距服从负指数分布; 在合流段L₂, 即x₁~x₂段内主路外侧车道车流车头时距服从2阶Erlang分布; 在合流段L₃, 即x₂~L段内主路外侧车道车流车头时距服从3阶Erlang分布。高速公路合流区的上匝道交通量可以通过对式(8)~(10)进行分段积分获得, 记整个合流区的上匝道交通量为V_m, 则

$\begin{array}{l}V{}_{\text{m}}=\frac{1}{L}[{\displaystyle {\int }_0^{x{}_1}V}{}_{\text{m}1}(x)\text{d}x+{\displaystyle {\int }_{x{}_1}^{x{}_2}V}{}_{\text{m}2}(x)\text{d}x+\\ {\displaystyle {\int }_{x{}_2}^{L}V}{}_{\text{m}3}(x)\text{d}x](11)\\ \text{记}B=a{}_{2}V{}_{\text{z}}+a{}_{3}V{}_{\text{r}}+a{}_4\\ \text{则}V{}_1(x)=a{}_{1}x+B\end{array}$

在0~x₁段内, 将式(8)代入∫₀^x₁V_m1(x)dx得

∫₀^x₁ $V{}_{\text{m}1}(x)\text{d}x=3600{}^2\frac{\text{e}{}^{-t{}_{0}B/3600}}{a{}_{1}t{}_{0}t{}_{\text{f}}}(1-\text{e}{}^{-a{}_{1}t{}_{0}x{}_1/3600})(12)$

在x1~x2段内, 将式(9)代入∫x2x1Vm2(x)dx得

$\begin{array}{l}{\displaystyle {\int }_{x{}_1}^{x{}_2}V}{}_{\text{m}2}(x)\text{d}x=\frac{1800}{a{}_{1}t{}_{\text{f}}}[\left(a{}_{1}x{}_1+B+\frac{5400}{t{}_0}\right)\text{e}{}^{-\frac{(a{}_{1}x{}_1+B)t{}_0}{1800}}-\\ \left(a{}_{1}x{}_2+B+\frac{5400}{t{}_0}\right)\text{e}{}^{-\frac{(a{}_{1}x{}_2+B)t{}_0}{1800}}](13)\end{array}$

在x₂~L内, 将式(10)代入∫^L_x2V_m3(x)dx得

${\displaystyle {\int }_{x{}_2}^{L}V}{}_{\text{m}3}(x)\text{d}x=\frac{\text{e}{}^{-Bt{}_0/1200}}{t{}_{\text{f}}}(C{}_1+C{}_2+C{}_3)(14)$

C₁=-a₁t₀(L²e^{-a₁t₀L/1 200}-x ${}_2^2$ e^{-a₁t₀x₂/1 200})/2

C₂=-(t₀B+3 600)(Le^{-a₁t₀L/1 200}-x₂e^{-a₁t₀x₂/1 200})

C₃=-1 200(t₀²B²/2 400+3t₀B+7 200)·(e^{-a₁t₀L/1 200}-e^{-a₁t₀x₂/1 200})/a₁t₀

将式(12)~(14)代入式(11)得

1.3.3   直接式汇入匝道情形分析

当对角匝道车辆驶入主路为直接汇入时, 由于汇入段长度较短, 可以根据主路外车道的车头时距分布状况, 直接采用式(8)~(10)分别计算当主路外车道的车头时距分布分别为负指数分布、2阶Erlang分布、3阶Erlang时对角匝道可驶入主路的适应交通量。

2.   驶入对角匝道左转车流适应交通量

在对角匝道上, 来自另一主线方向的左、右转车流在此合流, 合流点见图 1中的M₂点, 合流区2见图 3。在此合流区, 右转车流为主要车流, 左转车流需要寻找右转车流中的间隙从右转车流左侧进行汇合。左侧合流与右侧合流类似, 可以采用间隙接受理论进行分析, 但由于驾驶习惯以及中国车辆中驾驶员的位置等原因, 左侧合流的临界间隙和随车时距要比右侧合流时大。由于对角匝道上左转车辆合流一般采用直接汇入式, 合流区长度较短, 采用式(8)~(10)计算左转车流汇入的适应交通量。在此合流区, 记右转车流交通量为V'_r, 当右转车流的车头时距分别服从负指数分布、2阶Erlang分布、3阶Erlang分布时, 可得左转车流汇入的适应交通量V₁₁、V₁₂、V₁₃分别为

$\begin{array}{l}V{}_{11}=3600\frac{\text{e}{}^{-V^{\prime }{}_{\text{r}}t{}_0/3600}}{t{}_{\text{f}}}(16)\\ V{}_{12}=\frac{\text{e}{}^{-V^{\prime }{}_{\text{r}}t{}_0/1800}}{t{}_{\text{f}}}[V^{\prime }{}_{\text{r}}t{}_0+3600](17)\\ V{}_{13}=\frac{V^{\prime }{}_{\text{r}}^2\text{e}{}^{-V^{\prime }{}_{\text{r}}t{}_0/1200}}{2400t{}_{\text{f}}}\left(t{}_0^2+\frac{4800t{}_0}{V^{\prime }{}_{\text{r}}}+\frac{8640000}{V^{\prime }{}^2{}_{\text{r}}}\right)(18)\end{array}$

图  3  合流区2

Figure  3.  Merging area 2

下载: 全尺寸图片 幻灯片

另外, 驶入对角匝道的左右转车流交通量还应满足对角匝道驶入主路的交通量条件约束, 记V₁为对角匝道上可汇入的左转交通量, 则

$V^{\prime }{}_{\text{r}}+V{}_1\le V{}_{\text{m}}$

考虑到驾驶习惯、安全性等原因, 在高速公路匝道设计中次要车流从主要车流左侧汇入的情况较少, 但由于用地条件限制等原因需采用左侧汇入时, 除了考虑交通量条件之外, 还应从用地条件、匝道半径等方面进行详细分析。

3.   算例分析

以京津塘高速公路杨村上匝道为例, 分析该匝道作为对角匝道布设的对角匝道适应交通量以及对角匝道上左转车流汇入的适应交通量。合流区点M₁处的传感器布设见图 4。

图  4  传感器布设

Figure  4.  Sensor positions

下载: 全尺寸图片 幻灯片

经调查得到各传感器位置交通量及车型比例状况见表 1。由表 1可知, 合流区主路1车道车头时距在0~84 m范围内服从负指数分布, 84~200 m范围内服从2阶Erlang分布。本文取x₁、x₂分别为84、200。

通过对调查数据的回归分析得合流区主线1车道交通量模型系数^[8]a₁、a₂、a₃、a₄分别为0.678、-0.142、0.367、158, 则

V₁(x)=0.678x-0.142V_z+0.367V_r+158

由表 1得V_z为561 pcu·h^-1, V_r为240 pcu·h^-1, 则B等于166.40。取t_c为4 s, t_f为2 s, 则t₀等于3。由式(15)可得该入口匝道上匝道适应交通量为

$V{}_{\text{m}}=\frac{1}{200}\left[{\displaystyle {\int }_0^{84}V}{}_{\text{m}1}(x)\text{d}x+{\displaystyle {\int }_{84}^{200}V}{}_{\text{m}2}(x)\text{d}x\right]=1464$

表  1  交通流量及车型比例

Table  1.  Traffic volumes and vehicle type proportions

断面	车道	车型比例/%			流量/(veh·h-1)	流量/(pcu·h-1)
		小	中	大
加速车道入口	加速车道	20	64	16	162	240
距离加速车道鼻端40 m	加速车道	19	64	17	149	223
距离加速车道鼻端92 m	加速车道	22	64	14	79	115
距离加速车道鼻端140 m	加速车道	30	56	14	61	87
主线车道合流区初始端	1车道	30	61	9	148	205
	2车道	16	82	2	253	356
主线车道距离加速车道鼻端40 m	1车道	29	67	4	207	281
	2车道	14	82	4	269	384
主线车道距离加速车道鼻端92 m	1车道	23	61	16	261	383
	2车道	14	82	4	266	380
主线车道距离加速车道鼻端140 m	1车道	31	50	19	316	458
	2车道	39	58	3	283	369
主线车道合流区末端	1车道	21	58	21	328	496
	2车道	37	60	3	303	398
注: 该交通量条件下, 取合流区内小型车换算系数为1.000, 中型车换算系数为1.468, 大型车换算系数为2.140[10], 得到该表最后一列流量值。

下载: 导出CSV 

| 显示表格

即在该交通流状态下, 对角匝道驶入主路的适应交通量为1 464 pcu·h^-1。

假设该对角匝道上右转车流的驶入交通量V′_r分别为300、600、850 pcu·h^-1, 在合流区2, 当左转车流从左侧汇入右转车流时, 取t_c为5 s, t_f为3 s, 则由式(16)~(18)可得左转车流的适应交通量V₁₁、V₁₂、V₁₃分别为896、592、370 pcu·h^-1, 所得交通量均满足约束条件V′_r+V₁≤V_m。

4.   结语

(1) 通过对合流区主路外侧车道断面交通量与车头时距对应关系的推广, 得到当断面交通量小于350 pcu·h^-1时, 车头时距服从负指数分布; 位于350~699 pcu·h^-1及699~1 049 pcu·h^-1时, 分别服从2阶Erlang及3阶Erlang分布。

(2) 基于间隙接受理论原型, 得到合流区外侧车道x处车头时距分别服从负指数分布、2阶Erlang分布及3阶Erlang分布时, 该处可汇入主路的加速车道车辆数; 然后根据合流区外侧车道车头时距的区间分布状况, 通过在合流区内分段积分得到了对角匝道驶入主路的适应交通量。

(3) 考虑驶入对角匝道的右转车流交通量, 得到对角匝道上驶入的左转车流适应交通量, 并得到驶入对角匝道的左右转车流的约束条件。

(4) 研究表明, 对角匝道设置的交通量条件与主路交通量、匝道交通量、加速车道长度、合流区外侧车道车头时距的区间分布状况、汇合车辆的临界间隙和随车时距以及驶入对角匝道的左右转车流交通量有关。