ANP estimation algorithm of onboard navigation system based on numerical integration
-
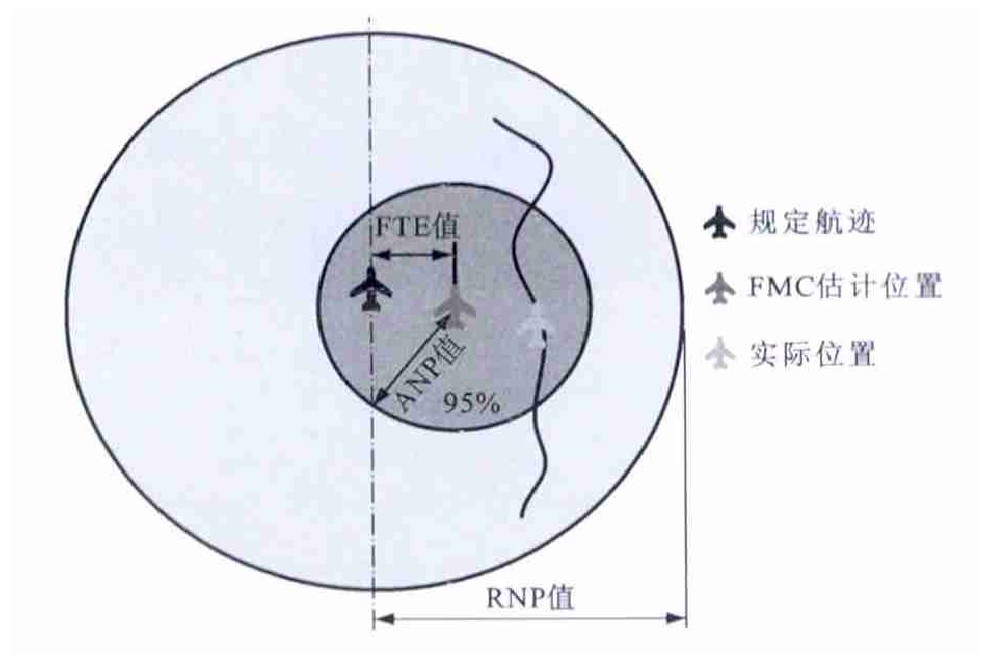
摘要: 为了准确评估飞机的实际导航性能, 确保飞行安全, 研究了基于性能导航运行方式下的机载综合导航系统的位置误差二维正态分布特性, 建立了ANP评估中飞机估计位置的误差模型, 推导了其概率误差圆的数值积分, 并提出了一种基于导航误差数值积分的机载综合导航系统ANP实时评估算法。以大型客机的典型综合导航方式为例, 对评估算法进行了仿真验证。仿真结果表明: ANP值能有效达到95%的误差估算精度, 算法能可靠地评估组合导航系统的实时误差特性, 具有较高的实际导航性能评估精度, 是一种切实有效的方法。Abstract: In order to accurately estimate the actual navigation performance (ANP) of plane and ensure the safety of flight, the two-dimensional normal distribution characteristic of position error for onboard integrated navigation system was studied based on the operation mode of performance based navigation (PBN).An error model of plane's estimated position in the estimation of ANP was established.The numerical integration of the probability of error circle was derived.An ANP real-time estimation algorithm of onboard integrated navigation system was proposed based on the numerical integration of navigation error.Then a simulation of the estimation algorithm was carried out based on a typical integrated navigation mode of an airliner.Simulation result indicates that the ANP value can effectively make the accuracy of error estimation reach 95%.The algorithm can estimate the real-time error characteristics of integrated navigation system authentically, has high ANP assessment precision for actual navigation performance, and is a kind of effective method.
-
0. 引言
航空电子技术的发展使机载设备不断更新, 导航精度不断提高, 促使基于性能导航(Performance Based Navigation, PBN) 的产生[1]。PBN规定了航空器在指定空域内或者沿航路、仪表程序飞行时的系统性能要求[2], 可以使航空器在任意两点之间精确飞行[3], 改善航空运行安全[4]。所需导航性能(Required Navigation Performance, RNP) 是PBN的一类基本导航规范, 指飞机在一个确定的航路、空域或区域内运行时所需的导航性能精度[5]。RNP类型决定了到规定航路点允许的距离误差[6], 即在95%的飞行时间内, 其导航系统的误差必须小于规定的RNP精度值, 因此, 要对机载导航系统的导航性能进行实时在线评估, 确保飞机安全飞行。
目前, 大型客机航电系统中常用的导航系统有惯性导航系统(Inertial Navigation System, INS)、全球定位系统(Global Positioning System, GPS)、测距导航系统(Distance Measuring Equipment, DME) 等。INS误差随时间而积累, GPS信号容易受到遮蔽和干扰, DME信号易受自然或人为干扰与破坏, 因此, 机载飞行管理系统会根据不同导航系统的输出进行融合与健康状态监测, 对其实际导航性能(Actual Navigation Performance, ANP) 进行实时、综合评估, 能够提高导航系统的余度和容错能力[7]。
国内外学者对RNP运行中设计规范与飞行航迹解算进行了大量研究: 王志学等研究了RNP AR仪表进近程序超障余度的设计准则[8]; 沈笑云等研究了RNP飞行程序和隧道结构, 提出了利用World Wind实现RNP飞行程序三维可视化的模拟飞行方法[9]; Ballin等以RNP运行为背景, 研究了飞行管理系统4D航迹的计算与导引, 分析了到达时间对航迹解算的约束条件[10]; McDonald等通过仿真试验研究了地形复杂的RNP运行环境下, GPS/IRS紧组合的可靠性设计要求[11]。目前, 国内外学者对RNP的研究多限于RNP运行效益分析与程序设计准则, 对实际导航性能实时评估方法的研究较少。孙淑光等提出了一种组合导航系统的ANP实时在线评估方法[12], 但由于积分的近似函数很快收敛, 与积分的真实值有一定的误差, 尤其当误差椭圆扁率较大时, 近似函数的精确度较差, 从而导致在进行ANP评估时求得的误差圆概率远离95%。为此, 本文针对机载多信息源综合导航系统, 提出一种基于导航误差数理特性的ANP评估改进方法, 利用数值积分逐步逼近95%概率误差圆的方式进行ANP评估, 可以有效提高ANP评估的精度。
1. 实际导航性能
RNP导航技术主要是利用高精度卫星导航系统和飞机机载导航系统来满足安全运行所要求的导航精度。在垂直方向上, 使用气压垂直导航(Barometric Vertical Navigation, Baro-VNAV) 等机载设备来确保符合高度限制, 满足垂直导航性能指标[13]。在水平方向中, 机载将ANP作为指标对水平精度进行评定[14]。
飞机沿预定航迹完成航路点间飞行的过程中, 由于飞行环境与飞机的操纵性等原因导致飞机的实际位置相对于预定航迹发生了偏离[15], 而其机载导航系统对实际位置的测量计算又存在误差[16]。ANP与RNP的关系见图 1, 估计位置为飞行管理计算机(Flight Management Computer, FMC) 估算出的位置, 飞行技术误差(Flight Technical Error, FTE) 为FMC估计位置与所需位置之间的差别, 小圆范围为估计位置的误差范围。可以看出, ANP利用概率的方式反映导航系统的导航性能, 定义为以FMC估计位置为中心的95%不确定度的圆的半径。
作为机组在RNP运行过程中非常重要的监控数据, ANP直接反映了航空器导航系统的工作状态, 并提供告警功能。ANP有时也被称为估计位置偏差, 由偏航误差和沿航迹误差决定, 但通常情况下偏航误差和沿航迹误差是不相等, 相应得到的是误差椭圆, 因此, 需要考虑将误差椭圆转换成误差圆。
2. 组合导航系统ANP评估算法
2.1 组合导航系统水平方向导航误差建模
利用卡尔曼滤波方法融合组合导航系统中各导航传感器的数据, 以导航参数误差量为状态量, 建立相应的误差方程, 得到误差状态的估计值, 再用误差状态的估计值校正系统, 最终得到组合系统的导航误差。其中包括经纬度误差, 为非水平面误差, 但因为经纬度误差角度比较小, 可以通过式(1) 转换为水平面内的误差x、y
式中: Δλ为经度误差; ΔL为纬度误差; R1、R2为地球参考椭球主曲率半径; h、L分别为飞机所在的高度与纬度; a为地球赤道平面半径, 为6 378 137m;b为地球参考椭球的椭圆率, 为1/298.259。
2.2 基于导航误差数值积分的ANP评估改进算法
通常水平面误差x、y为随机误差, 服从二维正态分布, 其概率密度函数为
式中: X为水平面误差; μ为X的均值向量; μx为x的均值; μy为y的均值; A为X的协方差矩阵; σx2为x的方差; σxy为x与y的协方差; σy2为y的方差。
函数f(x, y) 的分布曲面见图 2, 在点(μx, μy) 上达到最高峰。用平行于平面xOy的平面与该分布曲面相交, 并投影到xOy平面, 可得到一族同心的误差椭圆。在同一椭圆上的所有点, 其分布概率密度函数f(x, y) 是相同的。
对坐标系xOy分别作一个平移变换与一个旋转变换, 可以使误差椭圆中心平移到原点, 长短轴的方向与坐标轴重合, 而误差椭圆的形状保持不变, 得到标准化的误差椭圆Tk, k为误差椭圆缩放比率。当k取不同值时, Tk为一族分布密度不同的同心误差椭圆, 即
式中: E、F分别为k=1时, 标准误差椭圆的长、短半轴; θ为坐标轴的旋转角度。
经过上述标准化后, 二维正态分布的相关系数ρ为0, 概率密度函数为
点落入误差椭圆Tk内的概率P1为
当概率为0.95时, k取2.448, 即95%概率误差椭圆的长短半轴分别为2.448E、2.448F。
将误差椭圆Tk转换成误差圆Ck, 误差圆的概率P2为
式中: r为误差圆的半径; φ (y) 为积分区间函数。
式(6) 无法直接求出该积分的值, 因为对应的原函数不是初等函数。文献[12]使用误差椭圆扁率的简单初等函数作为误差圆的近似函数, 当扁率较大时, 误差圆的概率达不到95%。本文则分别2次利用数值积分中的复化Simpson公式进行计算, 将二重积分问题转变为求和问题。为简化式(6), 设中间函数为
将x区间[0, φ(y)]分成q个偶数等分, 步长s1为φ(y) /q, x2i-1、x2i为其等距节点, i=1, 2, …, q/2。根据复化Simpson公式, 对应每一个y得到
再将y区间[0, r]分成n个偶数等分, 步长s2为r/n, y2j-1、y2j为其等距节点, j=1, 2, …, n/2。由式(6) 推得
将式(8) 代入式(9), 即可得到积分值。可以证明步长s1、s2越小, 截断误差越小。当n、q趋近于无穷时, 用复化Simpson公式所求的近似值收敛于积分值, 而且算法具有数值稳定性。
95%概率误差圆Ck的半径必然在95%概率椭圆的长短半轴之间, 即位于区间[2.448F, 2.448E]中。而误差圆的概率随着半径r的增加而连续变大。所以可采用二分法的思想, 求得误差圆概率P2等于95%的半径r。该方法可以有效减少计算量, 提高计算效率, 便于实时评估机载综合导航系统ANP。
3. 仿真验证
构建民航客机多导航传感器综合仿真验证平台, 见图 3。根据机载各子导航系统的可用性及飞行不同阶段的RNP需求, 民航客机在飞行过程中会涉及不同组合导航模式的切换, 见图 4。以单独INS、INS/DME/DME (简称INS/DD)、INS/GPS、INS/GPS/DME/DME (简称INS/GPS/DD) 等4种导航模式为例进行仿真对比, 用本文提出的算法对上述导航方式进行ANP值的实时评估。
3.1 仿真条件
根据民航飞行要求, 按照起飞、爬升、巡航、下降、着陆5个阶段设计一条理想航迹, 见图 5。仿真时间为3 600s, 仿真IMU的器件噪声设置见表 1, GPS、DME/DME各子系统量测噪声误差设置见表 2。
表 1 仿真IMU器件的噪声参数Table 1. Noise parameters of simulated IMU devices
表 2 各子系统量测噪声误差Table 2. Measurement noise errors of subsystems
3.2 仿真结果分析
图 6为单独INS导航系统经纬度误差与实时ANP值。INS/DD组合导航采用双斜距组合方式, 将DME斜距偏置扩充为状态变量。通过卡尔曼滤波对各传感器数据进行最优融合, 得到经纬度误差, 代入到本文评估模型中, 计算出95%不确定度下的误差圆, 便得到了当前导航系统的ANP估值, 见图 7。采用同样方法得到INS/GPS组合导航系统的ANP估值, 见图 8。对INS/GPS/DD组合导航系统采用联邦卡尔曼滤波, 可得ANP估值, 见图 9。
大型客机在飞机飞行的不同阶段, 要求使用的传感器模式不同。由图 6可知, 纯惯性导航系统的误差随着时间的积累而发散, 所以不能单独用于RNP导航, 需要其他导航设备进行辅助导航。由图 7~9可以看出, 在GPS或DME/DME导航系统的辅助下, 能有效抑制惯导系统的发散, 并且INS/GPS/DD方式下的实际导航性能ANP最小, 即精度值最高, 其次是INS/GPS, 最后是INS/DD, 这是因为在组合导航系统中利用其他导航系统信息作为观测量进行滤波后, 其实际导航性能和辅助导航系统的精度密切相关, 而卫星系统的精度远高于DME/DME导航系统, 因此, 不同的导航子系统信息进行融合后, 其ANP值会不同, 传感器误差越大, ANP值越大。将导航系统的信息融合起来, 综合发挥各种导航系统的特点, 能提高导航信息精度, 更好地满足载体对导航系统的要求。经过ANP实时仿真验证, INS/GPS/DD组合方案能更有效抑制无线电的位置噪声, 综合导航系统精度得到进一步提高。选取INS/DD组合导航中t为514s进行具体分析, 此时经度误差为7.5m, 纬度误差为110.8m, 仿真求得ANP值为0.122nmile。通过数值积分验证得到误差圆的概率为95%。根据文献[12], 代入积分的近似函数求得ANP值为0.117nmile, 其误差圆概率仅为90%。
4. 结语
基于RNP技术的机载导航系统为飞机飞行过程提供一种安全、可靠的性能评估手段。本文建立了组合导航系统的水平误差模型, 利用二维随机误差的概率分布特性, 计算出水平位置误差95%不确定度的误差椭圆, 并由此得到ANP的评估算法。利用数值积分逼近积分真实值的方法, 在机载导航系统ANP实时评估方面具有较好的适应性。
-
[1] International Civil Aviation Organization. Performance based navigation manual[R]. Montreal: International Civil Aviation Organization, 2008. [2] 黄卫芳. 浅谈基于性能导航(PBN)[J]. 空中交通管理, 2007 (7): 10-16. https://www.cnki.com.cn/Article/CJFDTOTAL-XDDH201301004.htmHUANG Wei-fang. Performance based navigation[J]. Air Traffic Management, 2007 (7): 10-16. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XDDH201301004.htm [3] ECKSTEIN A. Automated flight track taxonomy for measuring benefits from performance based navigation[C]∥IEEE. Proceedings of the 2009Integrated Communications, Navigation and Surveillance Conference. Crystal City: IEEE, 2009: 1-12. [4] 吕小平. RNP/RNAV技术应用的效益分析[J]. 中国民用航空, 2008 (88): 42-44. https://www.cnki.com.cn/Article/CJFDTOTAL-MHJJ200804024.htmLU Xiao-ping. Benefit analysis of RNP/RNAV application[J]. China Civil Aviation, 2008 (88): 42-44. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-MHJJ200804024.htm [5] 倪育德, 肖山. RNAV和RNP技术研究[J]. 中国民用航空, 2010 (112): 63-65. https://www.cnki.com.cn/Article/CJFDTOTAL-MHJJ201004024.htmNI Yu-de, XIAO Shan. The research on RNAV and RNP technologies[J]. China Civil Aviation, 2010 (112): 63-65. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-MHJJ201004024.htm [6] JING Lin-lin, ZHANG Xue-jun. Lateral separation minima analysis based on required navigation performance[C]∥IEEE. 2010IEEE International Conference on Computer Science and Information Technology. Chengdu: IEEE, 2010: 144-148. [7] 彭仲仁, 刘晓锋, 张立业, 等. 无人飞机在交通信息采集中的研究进展和展望[J]. 交通运输工程学报, 2012, 12 (6): 119-126. doi: 10.3969/j.issn.1671-1637.2012.06.018PENG Zhong-ren, LIU Xiao-feng, ZHANG Li-ye, et al. Research progress and prospect of UAV applications in transportation information collection[J]. Journal of Traffic and Transportation Engineering, 2012, 12 (6): 119-126. (in Chinese). doi: 10.3969/j.issn.1671-1637.2012.06.018 [8] 王志学, 李晔. 基于RNP AR进近程序的最后进近航段分析[J]. 中国民航大学学报, 2012, 30 (5): 19-22, 33. doi: 10.3969/j.issn.1674-5590.2012.05.005WANG Zhi-xue, LI Ye. Analysis of final approach segment based on RNP AR approach[J]. Journal of Civil Aviation University of China, 2012, 30 (5): 19-22, 33. (in Chinese). doi: 10.3969/j.issn.1674-5590.2012.05.005 [9] 沈笑云, 赵瑞, 焦卫东, 等. 基于World Wind的RNP飞行程序三维可视化仿真[J]. 系统仿真学报, 2012, 24 (10): 2131-2135. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ201210021.htmSHEN Xiao-yun, ZHAO Rui, JIAO Wei-dong, et al. 3Dvisualization simulation of RNP flight procedure based on World Wind[J]. Journal of System Simulation, 2012, 24 (10): 2131-2135. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ201210021.htm [10] BALLIN M G, WILLIAMS D H, ALLEN B D, et al. Prototype flight management capabilities to explore temporal RNP concepts[C]∥IEEE. 27th IEEE Digital Avionics Systems Conference. Saint Paul: IEEE, 2008: 26-32. [11] MCDONALD J, KENDRICK J. Benefits of tightly coupled GPS/IRS for RNP operations in terrain challenged airports[C]∥IEEE. 2008IEEE/ION Position Location and Navigation Symposium. Washington DC: IEEE, 2008: 294-303. [12] 孙淑光, 戴博, 张鹏. 机载组合导航系统实际导航性能计算方法[J]. 控制工程, 2011, 18 (2): 262-266. doi: 10.3969/j.issn.1671-7848.2011.02.026SUN Shu-guang, DAI Bo, ZHANG Peng. Actual navigation performance calculation of onboard integrated navigation system[J]. Control Engineering of China, 2011, 18 (2): 262-266. (in Chinese). doi: 10.3969/j.issn.1671-7848.2011.02.026 [13] 张建华. 气压垂直导航安全性分析[J]. 空中交通管理, 2011 (2): 11-13, 16.ZHANG Jian-hua. Analysis of baro VNAV safety[J]. Air Traffic Management, 2011 (2): 11-13, 16. (in Chinese). [14] KLEIN K A, SHEPLEY J P. An analysis of automation for monitoring area navigation (RNAV) and required navigation performance (RNP) terminal operations[C]∥IEEE. 27th IEEE Digital Avionics Systems Conference. Saint Paul: IEEE, 2008: 2-12. [15] ZHAO Hong-sheng, XU Xiao-hao, ZHANG Jun, et al. Lateral flight technical error estimation model for performance based navigation[J]. Chinese Journal of Aeronautics, 2011, 24 (3): 329-336. [16] DONG Bing, LUO Xiao-li. Analysis of assessment method about the flight technical error based on Johnson curves[J]. Procedia Engineering, 2011, 17: 84-89. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 561
- HTML全文浏览量: 122
- PDF下载量: 1509
- 被引次数: 0
