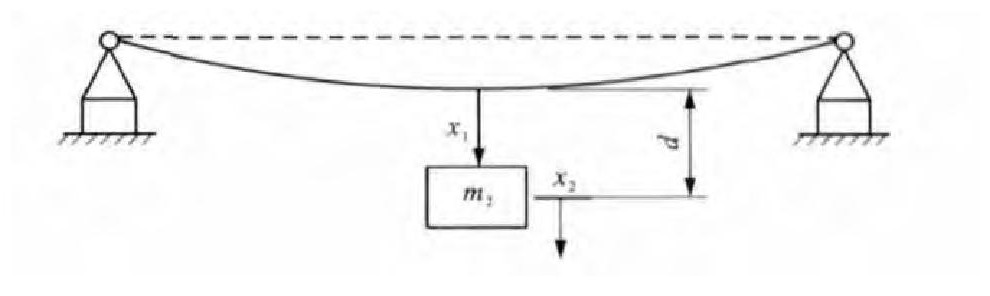
Small-scale similarity model of maglev-guideway coupling vibration
-
摘要: 将磁悬浮车轨耦合振动系统简化为单磁铁-Bernoulli-Euler梁模型, 设计了5种状态变量的反馈控制器, 分别在时、频域上研究了系统的动力学特性。依据相似理论建立了单磁铁车轨耦合系统的小比例模型, 推导了动力学系统的相似关系, 分析了小比例模型的相似特性。研究结果表明: 提出的磁悬浮控制方法利用轨道梁低阶模态与电磁铁振动信息得出控制器输出, 方法有效; 利用所设计的控制器, 系统能够在0.27s达到稳定状态, 最大超调量为2%;在单磁铁的车轨耦合振动系统中, 取其3阶模态即可较精确地反映其振动特性, 而当轨道梁各阶频率相差较大时, 对系统的低频特性分析, 在仅取第1阶模态时也可得出较精确的结果; 通过相似理论得到的小比例磁悬浮车轨耦合振动模型的动力学特性与原模型一致。Abstract: Simplified as a model composed of single magnet and Bernoulli-Euler beam, the maglevguideway coupling vibration system with 5-state-variable feedback controller was designed to study the dynamics performances of the system in the time and frequency domain. A small-scale model of single magnet-guideway coupling vibration system was established based on the similarity theory, its similarity performances were studied, and the similarity relationship of the dynamics systems was analyzed. Study result shows that the maglev control method, calculating the controller output with the vibration informations of guideway's low order mode and magnet, is effective and can keep the system stable. The step response of the system indicates that the developed controller can stabilize the system in 0.27 swith the overshot 2%. The first 3 order modes can be used to accurately describe the dynamics characteristics of coupling vibration system. For analyzing the lower frequency characteristics of the system, the first 1 order mode is sufficient when the large difference among the lower frequencies exists. The small-scale model obtained according to the similarity theory is coincident with the original model in the dynamics performances.
-
0. 引言
电磁型(EMS, Electromagnetic Suspension) 磁悬浮列车依靠电磁力使得车辆悬浮于轨道梁上, 避免了传统轮轨列车中的机械接触, 具有平稳舒适, 噪音低, 转弯半径小, 爬坡能力强等优点[1-2], 在城际高速和市内中低速交通中有着广阔的应用和发展前景。磁悬浮车辆中的悬浮电磁铁依靠电磁吸力悬浮于轨道梁之下, 在开环状态下, 电磁铁与轨道间隙变大时, 电磁力会迅速降低, 而间隙变小时, 电磁力又会快速增大, 因此, 必须对电磁力进行主动调节才能够确保车辆的稳定悬浮[3]。由于电磁力反作用在具有弹性的轨道梁上, 电磁力的变化必然引起轨道梁随之振动, 而轨道梁的振动又会改变间隙的大小, 进而影响电磁力的变化, 从而形成电磁铁-电磁力-轨道梁耦合振动系统。如果悬浮控制系统性能稍差, 电磁铁与轨道梁之间就可能产生强烈耦合振动, 影响磁浮车辆的稳定运行, 因此, 磁悬浮车辆的车轨耦合振动一直受到学术界的关注, 国内外学者对该问题进行了大量研究, 并取得了一定进展[4-10]。Yau分析了磁悬浮车辆运行状态下轨道梁基座对耦合振动特性的影响[4-5]; 王辉等分析了传统磁悬浮线路在解决车轨耦合振动中存在的弊端, 提出一种新型的磁悬浮线路设计方案[6-7]; Zhou等针对磁悬浮车轨耦合系统的自激振动现象提出了虚拟调谐质量阻尼器的概念[8]; Kong等建立5自由度的EMS车辆模型, 将轨道梁等效为Bernoulli-Euler梁, 研究了不同车速与质量下的车轨耦合系统的动力学响应特性[9]。然而, 由于磁悬浮系统规模庞大, 造价高昂, 多数的研究仅停留在理论分析和仿真的阶段。虽然国内外已经建成了数条磁悬浮试验线路, 但要进行相关的试验和测试仍会耗费大量的人力和物力。基于相似理论的模型试验方法不仅使得在实验室来完成大型系统的动力学试验成为可能, 而且也克服了原型试验中存在的费用高, 周期长, 现场测试条件差等问题。目前, 该方法已在公路交通的车桥耦合振动的研究中得到应用[10-13], 而磁悬浮车辆的车轨耦合振动问题却鲜见报道。为此, 本文在对磁悬浮车轨耦合振动系统研究的基础上, 基于相似理论, 对磁悬浮系统的电磁铁、轨道梁与电磁力进行相似, 推导出相似关系, 得到在动力学特性上一致的小比例试验台模型, 为磁悬浮车轨耦合振动问题的研究提供一种试验手段。
1. 振动系统模型的建立
磁悬浮列车一般是由多个悬浮点支撑, 但通过解耦, 悬浮系统可以分解为单个悬浮磁铁的控制问题, 所以单铁悬浮系统是磁悬浮系统的基本单元, 分析单铁悬浮系统的动态模型和动态特性比分析多磁铁系统更具通用性。将磁悬浮车轨耦合系统简化为图 1的单铁-弹性轨道模型, 以研究磁悬浮列车在弹性轨道上的动力学特性。图 1中: m2为电磁铁质量; x1、x2分别为轨道梁和电磁铁相对于平衡位置的垂向位移; d为悬浮间隙。
1.1 电磁力
单铁悬浮系统的瞬间电磁悬浮力F为[14]
式中: μ为真空磁导率; n为线圈匝数; A为电磁铁极面积; I为线圈中的实际电流。
将式(1) 在电磁铁悬浮平衡位置处线性化, 可得
式中: P1、P2分别为气隙系数和电流系数。
电磁铁线圈两端电压与电流的关系为
式中: R为电磁铁电阻; L、η分别为平衡点处的电磁铁电感和漏磁率; v为电磁铁两端电压。
1.2 轨道梁与悬浮电磁铁的动力学方程
在车轨耦合振动分析中, 轨道梁一般被简化为Bernoulli-Euler梁, 其动力学特性可用各阶振型函数与模态坐标的乘积的叠加来描述, 其形式为
式中: qi为梁的第i阶模态坐标; Δi为梁的第i阶振型函数。
通过求解如下二阶微分方程得到qi与Δi
式中: pi、ξi分别为第i阶模态频率和阻尼比。
电磁铁的力学方程为
式(6) 两边对时间t求导后整理得到
由式(1) ~ (7) 可得单磁铁车轨耦合振动系统的状态空间方程为
式中: Xr为状态变量; Yr为输出变量; w为轨道梁垂向激扰; Ar、Br、Cr、Nr分别为系统矩阵、输入矩阵、输出矩阵和干扰矩阵。
2. 控制器设计
控制系统大多采用反馈控制形式。在现代控制理论中, 其反馈信息是由系统的状态变量组合而成, 但并非所有的状态变量在物理上都能测到, 一般在确保系统能观性的前提下, 可以通过状态观测器, 利用可测得的物理量来获取系统的状态变量。本文利用加速度传感器和间隙传感器, 通过测量得到的电磁铁加速度与悬浮间隙获取系统的其他状态变量。设计出渐近型状态观测器见图 2中的虚线框部分, 其中: G为观测器的输出误差反馈矩阵; XO、YO分别为观测器的状态变量与输出变量; AO、BO、CO分别为观测器矩阵、输入矩阵与输出矩阵; K为反馈系数向量。
由连续梁的振动理论可知, 高阶模态下梁的阻尼衰减作用较强, 且振动节点较多, 相对低阶模态振动, 其对梁的综合振动特性影响较小。此外, 选取过多的模态阶数构造状态观测器会使得控制系统过于复杂, 增加控制成本, 因而, 本文在构造状态观测时仅选择第1阶模态来描述梁的振动特性。在状态观测器中, 选择状态变量为
式中:
由图(2) 可得
反馈控制电压为
控制器的反馈系数向量为
选取
3. 仿真结果分析
为验证控制策略的有效性, 在式(8) 描述的单磁铁车轨耦合振动仿真模型中, 取模型中水泥梁各阶自振频率与阻尼比按照1.00、2.70、5.39、……的倍数关系增加[15], 其他参数取值见表 1。
表 1 车轨耦合振动模型参数Table 1. Parameters of vehicle-guideway coupling vibration model
在以电磁铁悬浮于轨道梁跨中位置时的系统为对象(下同), 来研究车轨耦合系统的动力学特性, 取G和K分别为
设定电磁铁初始位置偏离平衡点5mm, 仿真时间为1s, 分别取轨道梁的前1、3、5阶模态时, 仿真得到系统的响应曲线见图 3~6。
由图 3~6可知: 系统在较短的时间内即可恢复到平衡状态; 若设定稳定域为2%, 则悬浮间隙在0.27s即可达到稳定状态, 最大超调量为2%, 仿真结果证明了控制策略的有效性; 在系统的时域响应曲线中, 轨道梁的高阶模态对悬浮间隙、电磁铁加速度与轨道梁位移几乎没有影响; 不同的模型中, 轨道梁加速度响应曲线变化趋势一致, 但相对于仅考虑第1阶轨道梁模态的模型, 包含了高阶模态的模型中梁的加速度响应含有高频振动成分。
根据式(1) ~ (10), 求得悬浮间隙、电磁铁加速度、轨道梁位移与轨道梁加速度对激扰w的频率域响应曲线分别见图 7~10, 向应函数分别为
式中: X1为轨道梁位移的傅立叶变换; X2为电磁铁悬浮位移的傅立叶变换;
由图 7~10可知: 不同模型中的悬浮间隙、电磁铁加速度与轨道梁位移的频域响应特性非常接近, 即轨道梁高阶模态对这3种函数频域响应的影响可以忽略; 激扰频率与梁的自振频率接近时, 梁的振动加剧, 其位移响应与加速度响应在自振频率附近均出现突变现象, 但高阶模态频率处突变较小, 以考虑前5阶模态的模型为例, 频率为107.4Hz与幅值为1mm的激扰所产生的梁振动加速度响应仅为0.27m·s-2。综合上述结果可知, 在单磁铁的车轨耦合振动系统中, 取轨道梁的前3阶模态可较精确地反映出轨道梁的振动特性; 对系统的低频特性分析时, 如电磁铁的低频跟随特性, 仅取第1阶模态也可得出较精确的结果, 尤其当轨道梁各阶频率相差较大时。
4. 基于相似理论的单磁铁车轨耦合振动模型
4.1 轨道梁模型的简化
如今轨道梁的跨度越来越大, 在实验室进行1∶1的磁悬浮车辆的车轨耦合振动试验并不现实; 采用小比例连续梁来模拟轨道梁, 仅能确保二者的第1阶固有频率相近, 而高阶频率很难保证, 且小比例梁的加工与安装精度要求较高。在单磁铁的车轨耦合振动系统中, 本文仅取轨道梁的第1阶模态也可近似地反映轨道梁的振动特性, 由式(5) 得
对式(12) 两边同乘以Δ1 (Δ1≠0), 并令x1为q1Δ1, 则轨道梁在某一位置处的振动特性为
对式(13) 作进一步变换可得
式中: m1、k、c分别为轨道梁的质量、刚度与阻尼。
式(14) 与质量块的单自由度振动方程相同, 因此, 在仅取第1阶模态的条件下, 可将磁悬浮车辆的单磁铁车轨耦合振动模型简化为图 11的系统, 以集中质量与弹簧阻尼元件来模拟连续梁在某一位置处的振动特性。由于电磁铁未作改动, 因此, 电磁力相关参数不变, 其他参数见表 2。
表 2 车轨耦合振动系统的等效参数Table 2. Equivalent parameters of vehicle-guideway coupling vibration model
4.2 电磁铁与轨道梁模型的相似关系
在等效后的系统中, 轨道梁与电磁铁质量较大, 在实验室搭建这样的模型较困难。由于主要考察电磁铁与轨道梁的耦合振动问题和悬浮控制系统的稳定特性, 可通过小比例模型来进行模拟。在搭建小比例试验台模型时应保证小比例系统与原系统动力学特性相同, 为此, 本文基于相似理论, 分别对电磁铁、轨道梁的动力学模型及电磁力进行了相似处理。相似处理前后轨道梁固有频率与阻尼比不变, 从而保证了轨道梁的振动特性不变; 相似处理前后电磁铁与轨道梁的质量(等效) 比不变, 从而确保小比例模型中轨道梁与悬浮电磁铁惯性质量的相互影响与实际线路中的相同。小比例试验台中各主要参数满足如下关系(带有下标e的变量为小比例模型中对应于原系统模型的相应参数)
令
4.3 电磁力的相似关系
在小比例模型中, 由于电磁铁体积变小, 电磁力参数也相应更改。忽略漏磁率的影响, 即令η=0, 则由式(8) 可得
设带下标的λ为对应物理量的相似比例系数, 并令相似处理前后时间尺度不变, 即时间的相似比例系数λt=1, 由式(16) 可得
由式(17) 可得
同理, 由电磁铁两端电压与电流之间关系
可得
式中: IN、dN分别为稳定状态的线圈电流与悬浮间隙。
由于工程实际中电磁铁的稳定悬浮间隙较小, 一般为10mm (或8mm), 因此, 相似比例系数
由式(17)、(21) 可得
至此, 建立了小比例模型与原系统中各对应物理量相似比例关系, 并以电磁铁质量相似比例系数
4.4 小比例模型与原模型的对比
在小比例试验台搭建时, 电磁铁质量的大小直接决定着系统稳定时所需电磁力的大小, 也决定了试验台的物理可实现性, 因此, 其相似比例系数应根据试验条件合理选择。根据表 1、2中数据, 取相似比例系数
表 3 小比例模型参数Table 3. Parameters of small-scale model
为验证小比例模型与原系统(轨道梁前1阶模态) 动力学特性的一致性, 计算了2种模型的幅频特性。小比例模型中电磁铁漏磁率不易控制, 且受试验环境影响较大, 图 12~15中给出了不同漏磁率下小比例模型的频域响应结果。
图 13 电磁铁加速度频域响应的比较Figure 13. Frequency domain response comparison of electromagnet accelerations
图 14 轨道梁位移频域响应的比较Figure 14. Frequency domain response comparison of guideway displacements
图 15 轨道梁加速度频域响应的比较Figure 15. Frequency domain response comparison of guideway accelerations由图 12~15可以看出, 通过相似理论得到的小比例磁悬浮车轨耦合振动模型与原模型在动力特性上保持一致; 小比例模型中漏磁率的增加会使得电磁铁加速度高频响应值增大, 但对悬浮间隙与轨道梁的振动响应影响较小。
5. 结语
磁悬浮控制方法利用轨道梁低阶模态与电磁铁振动信息有效得出控制器输出, 能够实现磁悬浮车辆的稳定悬浮; 在单磁铁的车轨耦合振动系统中, 若将轨道梁简化为简支的Bernoulli-Euler梁, 取其3阶模态即可较精确地反映出其振动特性; 对系统的低频特性分析时, 仅取第1阶模态可得出较精确的结果; 通过相似理论得到的小比例磁悬浮车轨耦合振动模型能够在动力学特性上与原模型一致, 为磁悬浮车轨耦合振动问题的研究提供一种小比例模型的搭建方法。
-
图 13 电磁铁加速度频域响应的比较
Figure 13. Frequency domain response comparison of electromagnet accelerations
图 14 轨道梁位移频域响应的比较
Figure 14. Frequency domain response comparison of guideway displacements
图 15 轨道梁加速度频域响应的比较
Figure 15. Frequency domain response comparison of guideway accelerations
表 2 车轨耦合振动系统的等效参数
Table 2. Equivalent parameters of vehicle-guideway coupling vibration model
下载: 导出CSV
-
[1] LEE H W, KIM K C, LEE J. Review of maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42 (7): 1917-1925. doi: 10.1109/TMAG.2006.875842 [2] YAN Lu-guang. Suggestion for selection of maglev option for Beijing-Shanghai high-speed line[J]. IEEE Transactions on Applied Superconductivity, 2004, 14 (2): 936-939. doi: 10.1109/TASC.2004.830324 [3] ZHOU Dan-feng, HANSEN C H, LI Jie, et al. Review of coupled vibration problems in EMS maglev vehicles[J]. International Journal of Acoustics and Vibration, 2010, 15 (1): 10-23. [4] YAU J D. Vibration control of maglev vehicles traveling over a flexible guideway[J]. Journal of Sound and Vibration, 2009, 321 (1/2): 184-200. [5] YAU J D. Response of a maglev vehicle moving on a series of guideways with differential settlement[J]. Journal of Sound and Vibration, 2009, 324 (3): 816-831. [6] 王辉, 钟晓波, 沈钢. 一种新型磁悬浮线路设计方案及悬浮控制方法[J]. 同济大学学报: 自然科学版, 2013, 41 (7): 1112-1118. doi: 10.3969/j.issn.0253-374x.2013.07.026WANG Hui, ZHONG Xiao-bo, SHEN Gang. A new maglev line system design and control strategy[J]. Journal of Tongji University: Natural Science, 2013, 41 (7): 1112-1118. (in Chinese). doi: 10.3969/j.issn.0253-374x.2013.07.026 [7] 崔鹏, 李杰, 张锟. 基于补偿反馈线性化的悬浮控制器设计[J]. 铁道学报, 2010, 32 (2): 37-40. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201002009.htmCUI Peng, LI Jie, ZHANG Kun. Design of the suspension controller based on compensated feedback linearization[J]. Journal of the China Railway Society, 2010, 32 (2): 37-40. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201002009.htm [8] ZHOU Dan-feng, LI Jie, HANSEN C H. Application of least mean square algorithm to suppression of maglev trackinduced self-excited vibration[J]. Journal of Sound and Vibration, 2011, 330 (24): 5791-5811. doi: 10.1016/j.jsv.2011.07.021 [9] KONG E, SONG J S, KANG B B, et al. Dynamic response and robust control of coupled maglev vehicle and guideway system[J]. Journal of Sound and Vibration, 2011, 330 (25): 6237-6253. doi: 10.1016/j.jsv.2011.05.031 [10] 王辉, 钟晓波, 沈钢. 弹性轨道梁上磁悬浮控制方法[J]. 交通运输工程学报, 2013, 13 (5): 33-38, 46. http://transport.chd.edu.cn/article/id/201305005WANG Hui, ZHONG Xiao-bo, SHEN Gang. Control strategy of maglev on elastic track[J]. Journal of Traffic and Transportation Engineering, 2013, 13 (5): 33-38, 46. (in Chinese). http://transport.chd.edu.cn/article/id/201305005 [11] 任永明. 公路桥梁车桥耦合振动模型试验研究[D]. 南昌: 华东交通大学, 2011.REN Yong-ming. The model test study of highway bridge on vehicles-bridge coupling vibration[D]. Nanchang: East China Jiaotong University, 2011. (in Chinese). [12] 郑亮. 高墩大跨桥梁车桥耦合振动模型试验研究[D]. 西安: 长安大学, 2011.ZHENG Liang. Model test on vehicle-bridge coupled vibration for the long-span bridge with high-pier[D]. Xi'an: Chang'an University, 2011. (in Chinese). [13] GUI Shui-rong, CHEN Shui-sheng, REN Yong-ming. Study on vibration test of the scale-model system for highway bridge-vehicle interaction according to the similarity law[C]∥IEEE. 2011International Conference on Remote Sensing, Environment and Transportation Engineering. Nangjing: IEEE, 2011: 1735-1739. [14] MEISINGER R. Control systems for flexible maglev vehicles riding over flexible guideways[J]. Vehicle Dynamic System, 1975, 4 (2/3): 200-202. [15] 田宇. 考虑车轨相对位置的车轨耦合振动控制研究[D]. 长沙: 国防科技大学, 2011.TIAN Yu. Research on the vehicle-guideway coupled vibration control considering the relative position between the vehicle and the guideway[D]. Changsha: National University of Defense Technology, 2011. (in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 616
- HTML全文浏览量: 123
- PDF下载量: 2498
- 被引次数: 0
