基于DSPN的高速磁浮运控系统越区切换模型

曹源; 张玉琢; 马连川; 孙雅晴; 穆建成

基于DSPN的高速磁浮运控系统越区切换模型

1.
北京交通大学轨道交通运行控制系统国家工程研究中心, 北京 100044
2.
北京交通大学电子信息工程学院, 北京 100044
3.
上海自仪泰雷兹交通自动化系统有限公司, 上海 201206
4.
国家铁路局科技与法制司, 北京 100891

基金项目:

国家863计划项目 2012AA112001

国家自然科学基金项目 51305021

国家自然科学基金项目 U1334211

中国铁路总公司科技研究开发计划项目 2013X013-D

详细信息

作者简介:
曹源(1982-), 男, 河南开封人, 北京交通大学讲师, 工学博士, 从事列车运行控制系统研究

中图分类号: U283
计量
- 文章访问数: 574
- HTML全文浏览量: 83
- PDF下载量: 980
- 被引次数: 0
出版历程
- 收稿日期: 2013-12-08
- 刊出日期: 2014-04-25

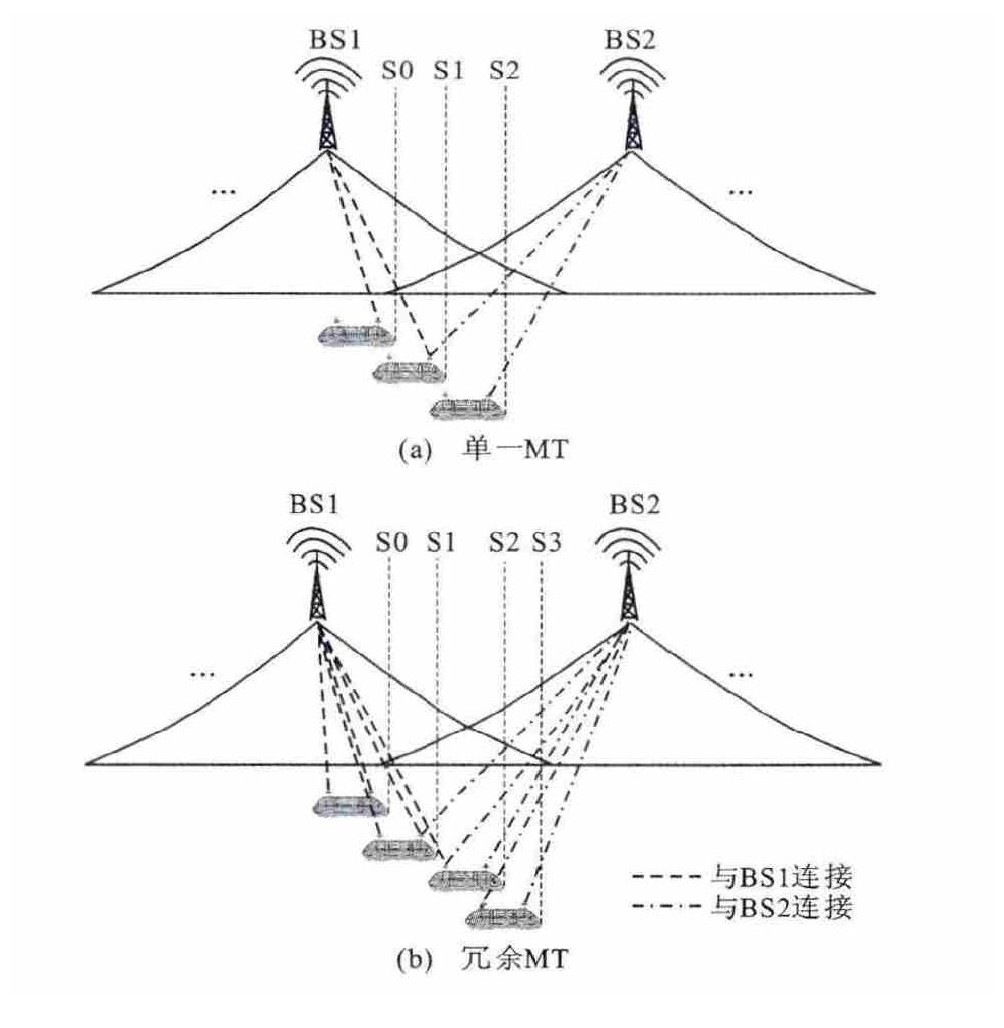
Handoff model of operation control system of high-speed maglev based on DSPN

1.
National Engineering Research Center of Rail Transportation Operation and Control System, Beijing Jiaotong University, Beijing 100044, China
2.
School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China
3.
Thales Saic Transportation System Limited Company, Shanghai 201206, China
4.
Department of Science-Technology and Law, National Railway Administration of the People's Republic of China, Beijing 100891, China

More Information

Author Bio:
CAO Yuan (1982-), male, lecturer, PhD, +86-10-51688537, ycao@bjtu.edu.cn

摘要

摘要: 考虑38GHz毫米波通信中断与信道占用因素, 依据磁浮运控系统越区切换流程建立了确定与随机Petri网(DSPN) 模型, 对单一移动终端(MT) 和冗余MT两种结构进行了比较, 研究了基站间距和列车运行速度对单一MT和冗余MT两种结构越区切换可靠性的影响。研究结果表明: 冗余MT越区切换性能明显优于单一MT, 后者的停车概率约为前者的3×10⁴倍; 越区切换成功率随列车运行速度的提高而降低, 随基站间距的减小而降低; 在极端情况下, 即列车以500km·h^-1运行, 且相邻基站间距为500m, 冗余MT和单一MT越区切换成功率只有98.50%和97.85%。研究结论为磁浮运控系统车地通信子系统的服务质量优化与移动小区设置提供了依据。
- 列车运行控制系统 /
- 越区切换 /
- 确定与随机Petri网 /
- 高速磁浮 /
- 车地通信 /
- 可靠性
Abstract: Considering the factors of the communication outage of 38GHz millimeter wave and channel occupancy, deterministic and stochastic Petri nets model (DSPN) was developed based on the handoff process of maglev operation control system.The structures of single mobile terminal (MT) and redundant MT were compared.The effects of base station interval and train running velocity on the handoff reliabilities of single MT and redundant MT were investigated.Investigation result indicates that the handoff performance of redundant MT is significantly higher than that of single MT, the parking probability of single MT is approximate 3×10⁴ times of that of redundant MT.The handoff success rate reduces with the increase of train running velocity and the decrease of base station interval.In the special case, in which the train running velocity is 500 km·h^-1 and the base station interval is 500 m, the handoff success rates of redundant MT and single MT are only 98.50% and 97.85% respectively. Research result provides basis for the QoS optimization of train-ground communication subsystem in maglev operation control system and mobile cell setting.
- train operation control system /
- handoff /
- DSPN /
- high-speed maglev /
- train-ground communication /
- reliability

HTML全文

图 1 越区切换场景

Figure 1. Handoff scenarios

下载: 全尺寸图片幻灯片

图 2 DSPN中的元素

Figure 2. Elements of DSPN

下载: 全尺寸图片幻灯片

图 3 单一MT越区切换DSPN模型

Figure 3. Handoff DSPN model of single MT

下载: 全尺寸图片幻灯片

图 4 冗余MT越区切换DSPN模型

Figure 4. Handoff DSPN model of redundant MT

下载: 全尺寸图片幻灯片

图 5 越区切换成功率与基站间距的关系

Figure 5. Relationship between handoff success rate and base station interval

下载: 全尺寸图片幻灯片

图 6 越区切换成功率与列车运行速度的关系

Figure 6. Relationship between handoff success rate and train running velocity

下载: 全尺寸图片幻灯片

图 7 停车概率与基站间距的关系

Figure 7. Relationship between parking probability and base station interval

下载: 全尺寸图片幻灯片

表 1 库所与变迁的意义

Table 1. Significances of places and transitions

下载: 导出CSV

表 2 指数变迁和确定变迁取值

Table 2. Values of exponential transitions and deterministic transitions

下载: 导出CSV

表 3 瞬时变迁的哨函数

Table 3. Guard functions of immediate transitions

下载: 导出CSV

参考文献(19)

[1]	杨光, 唐祯敏. 几种典型轨道交通运行控制系统的比较研究[J]. 铁道学报, 2009, 31 (1): 82-87. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200901020.htm YANG Guang, TANG Zhen-min. Analysis of similarities and differences of operation control systems among several typical modes of rail traffic[J]. Journal of the China Railway Society, 2009, 31 (1): 82-87. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200901020.htm
[2]	HOSSEINI M S, VAEZ-ZADEH S. Modeling and analysis of linear synchronous motors in high-speed maglev vehicles[J]. IEEE Transactions on Magnetics, 2010, 46 (7): 2656-2664. doi: 10.1109/TMAG.2009.2039999
[3]	ZHENG Wei, XU Hong-ze. Safety requirements parameter derivation for maglev train propulsion and protection systems based on stochastic Petri nets[C]//IEEE. 2009 International Conference on Measuring Technology and Mechatronics Automation. Zhangjiajie: IEEE, 2009: 507-510.
[4]	ZHU L, YU F R, NING B, et al. Handoff management in communication-based train control networks using stream control transmission protocol and IEEE 802.11p WLANs[J]. EURASIP Journal on Wireless Communications and Networking, 2012, 211: 1-16.
[5]	陈黎洁, 唐涛, 吕继东. CBTC越区切换中断时间分析[J]. 中国铁道科学, 2010, 31 (5): 125-129. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201005023.htm CHEN Li-jie, TANG Tao, LU Ji-dong. Analysis on the interruption time for CBTC handover[J]. China Railway Science, 2010, 31 (5): 125-129. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201005023.htm
[6]	XU Tian-hua, TANG Tao, GAO Chun-hai, et al. Dependability analysis of the data communication system in train control system[J]. Science in China Series E: Technological Sciences, 2009, 52 (9): 2605-2618. doi: 10.1007/s11431-009-0183-4
[7]	DUTTA A, LYLES B, SCHULZRINNE H, et al. Generalized modeling framework for handoff analysis[C]//IEEE. The 18th Annual International Symposium on Personal, Indoor and Mobile Radio Communications. Athens: IEEE, 2007: 1-5.
[8]	THOMSEN J M. Analysis of GSM handover using colored Petri nets[D]. Aarhus: University of Aarhus, 2003.
[9]	张友兵, 张波, 唐涛. 列控数据传输与GSM-R越区切换发生碰撞的建模与分析[J]. 铁道学报, 2013, 35 (5): 47-53. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201305008.htm ZHANG You-bing, ZHANG Bo, TANG Tao. Modeling and analyzing of data transmission colliding with GSM-R handover in train control system[J]. Journal of the China Railway Society, 2013, 35 (5): 47-53. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201305008.htm
[10]	曹源, 牛儒, 唐涛, 等. 基于SPN的越区切换模型分析[J]. 铁道学报, 2009, 31 (4): 3-4. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200904021.htm CAO Yuan, NIU Ru, TANG Tao, et al. Analysis of handover model based on stochastic Petri net[J]. Journal of the China Railway Society, 2009, 31 (4): 3-4. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200904021.htm
[11]	LUO Wan-tuan, ZHANG Rui-qiang, FANG Xu-ming. A COMP soft handover scheme for LTE systems in high speed railway[J]. EURASIP Journal on Wireless Communications and Networking, 2012, 211: 17-25.
[12]	张仿琪. 毫米波无线通信系统在高速磁浮交通中的应用[D]. 上海: 复旦大学, 2011. ZHANG Fang-qi. The application of millimeter communication system in high-speed maglev[D]. Shanghai: Fudan University, 2011. (in Chinese).
[13]	PLATTNER A. A millimeterwave communication system for maglev application[C]//IEEE. 1994 IEEE MTT-S International Microwave Symposium Digest. San Diego: IEEE, 1994: 745-748.
[14]	YANG Yu-sheng, ZHANG Chun-xi, QIU Hai-tao. Modeling and performance evaluation of IEEE-1394 bisochronous data transfer with DSPN[C]//IEEE. 2010 2nd International Conference on Advanced Computer Control. Shenyang: IEEE, 2010: 152-156.
[15]	郑伟. 磁悬浮列车跨系统运行Petri网模型[J]. 交通运输工程学报, 2012, 12 (2): 112-118. http://transport.chd.edu.cn/article/id/201202016 ZHENG Wei. Petri net model of maglev train running across different control systems[J]. Journal of Traffic and Transportation Engineering, 2012, 12 (2): 112-118. (in Chinese). http://transport.chd.edu.cn/article/id/201202016
[16]	李伟. 基于有色Petri网的无线闭塞中心子系统切换建模与验证[D]. 北京: 北京交通大学, 2009. LI Wei. The modeling and verification of RBC handover based on colored Petri nets[D]. Beijing: Beijing Jiaotong University, 2009. (in Chinese).
[17]	徐田华, 唐涛. 列车控制系统中数据通信子系统的帧丢失概率[J]. 中国铁道科学, 2008, 29 (3): 110-114. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200803022.htm XU Tian-hua, TANG Tao. Frame loss probability of data communication subsystem in train control system[J]. China Railway Science, 2008, 29 (3): 110-114. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200803022.htm
[18]	ZIMMERMANN A, HOMMEL G. A train control system case study in model-based real time system design[C]//IEEE. Proceedings of the International Parallel and Distributed Processing Symposium. Nice: IEEE, 2003: 1-8.
[19]	LONG Zhi-qiang, LU Zhi-guo, HUAN Shang, et al. Analysis and design in safeties and reliabilities of the suspension system of maglev train[C]//IEEE. Proceedings of the 5th World Congress on Intelligent Control and Automation. Hangzhou: IEEE, 2004: 1819-1823.