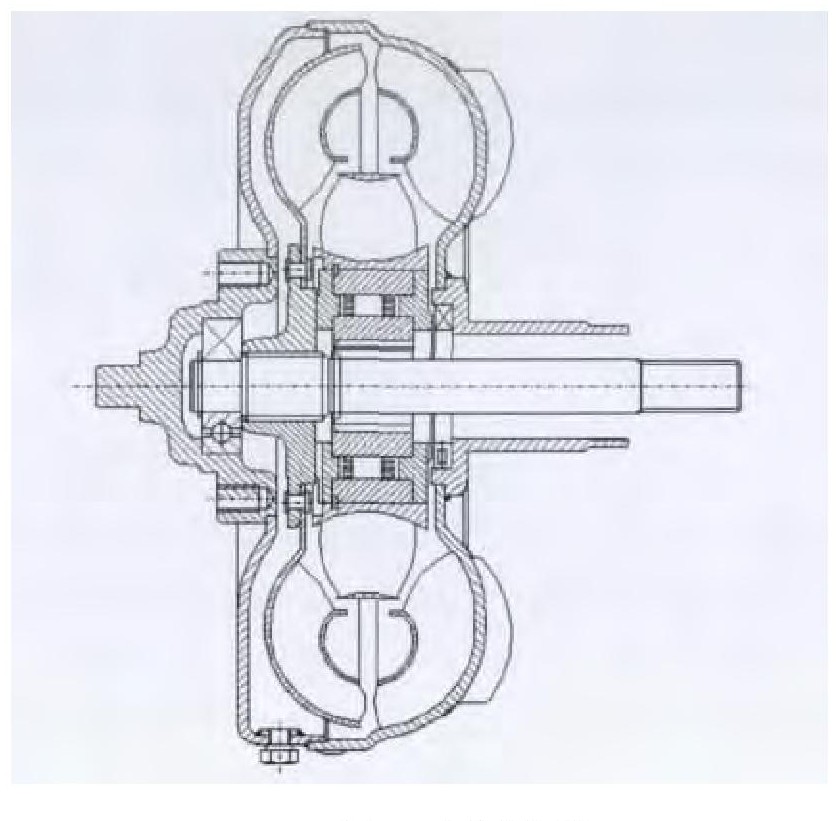
Design of turbine blades of torque converter based on reverse technology
Article Text (Baidu Translation)
-
摘要: 为了解决变矩器设计周期过长和对经验数据依赖过多的问题, 运用反求技术对冲压型涡轮叶片数据进行计算、分析, 在建立广义的液流环坐标系基础上, 提炼出涡轮叶形设计流线的数学表达式, 获得叶片内、外环加工点的准确坐标, 推导出新的变矩器原始特性表达式。根据计算结果制成新的涡轮叶片, 比较了装有新涡轮叶片的液力变矩器与原样机的特性。试验结果表明: 新设计的变矩器和原样机的效率和失速变矩仅降低了0.5%, 转矩系数降低了1%, 新叶片与原叶片的误差小于0.605 2%, 因此, 本文在环坐标系下得到变矩器环面和轴面方程式是准确的, 保证了产品的设计性能, 并缩短了研发周期, 拓宽了变矩器研发的新途径。Abstract: In order to shorten the design cycle of torque converter and reduce the dependence of experience in design, the reverse technology was used to calculate and analyze the data of turbine's stamping blades.Based on the generalized torus coordinate system of liquid flow, the mathematical expression of blade design baseline was deduced, the machine coordinates of blade were obtained accurately on both inside and outside rings, and the original characteristic expression of new torque converter was described.Then, new torque converter with designed blades was tested and compared with prototype.Test result indicates that new converter efficiency and torque ratio with new turbine blades are only 0.5% lower than prototype, and the torque coefficient is only 1% lower.The error between new blade and origin one is less than 0.605 2%.Therefore, the torus and axial surface equations obtained from torus coordinate system is accurate.This method offers a new choice to ensure the reliability of product and shorten its cycle in the design of torque converter.
-
Key words:
- vehicle engineering /
- torque converter /
- reverse technology /
- blade design /
- torus coordinate system
-
表 1 涡轮叶片外环点与内环点的坐标
Table 1. Coordinates of points on outer cycle and inner cycle of turbine blade
下载: 导出CSV
-
[1] DONG Y, LAKSHMINARAYANA B, MADDOCK D. Steady and unsteady flow field at pump and turbine exits of a torque converter[J]. Joumal of Fluids Engineering, 1998, 120 (3): 538-548. doi: 10.1115/1.2820696 [2] EJIRI E, KUBO M. Performance analysis of automotive torque converter elements[J]. Journal of Fluids Engineering, 1999, 121 (2): 266-275. doi: 10.1115/1.2822201 [3] SHIN S, CHANG H, ATHAVALE M. Numerical investigation of the pump flow in an automotive torque converter[J]. SAE Paper, 1999-01-1056. [4] BY R R, KUNZ R, LAKSHMINARAYANA B. NavierStokes analysis of the pump flow field of an automotive torque converter[J]. Journal of Fluids Engineering, 1995, 117 (1): 116-122. doi: 10.1115/1.2816800 [5] TSUJITA H, EJIRI E, MIZUKI S, et al. Analysis of flow within pump impeller of torque converter[J]. Transactions of the Japan Society of Mechanical Engineers, 1993, 59 (564): 2500-2508. doi: 10.1299/kikaib.59.2500 [6] DONG Y, KORIVI V, ATTIBELE P, et al. Torque converter CFD engineering part Ⅱ: performance improvement through core leakage flow and cavitation control[J]. SAE Paper, 2002-01-0884. [7] 褚亚旭, 马文星, 方杰, 等. 液力变矩器三维流动的计算[J]. 农业机械学报, 2005, 36 (8): 107-110. doi: 10.3969/j.issn.1000-1298.2005.08.028CHU Ya-xu, MA Wen-xing, FANG Jie, et al. Three dimensional flow calculation of hydrodynamic torque converter[J]. Transactions of the Chinese Society of Agricultural Machinery, 2005, 36 (8): 107-110. (in Chinese). doi: 10.3969/j.issn.1000-1298.2005.08.028 [8] 雷雨龙, 葛安林, 田华, 等. 基于内流场分析的液力变矩器改型设计[J]. 机械工程学报, 2006, 42 (2): 125-128. doi: 10.3321/j.issn:0577-6686.2006.02.024LEI Yu-long, GE An-lin, TIAN Hua, et al. Amending redesign of torque converter based on internal flow field simulation[J]. Chinese Journal of Mechanical Engineering, 2006, 42 (2): 125-128. (in Chinese). doi: 10.3321/j.issn:0577-6686.2006.02.024 [9] 魏巍, 闫清东. 液力变矩器叶栅系统三维优化设计方法研究[J]. 流体传动与控制, 2006 (4): 41-44, 48. doi: 10.3969/j.issn.1672-8904.2006.04.011WEI Wei, YAN Qing-dong. Research on three-dimensional optimization design method of torque converter casecade[J]. Fluid Power Transmission and Control, 2006 (4): 41-44, 48. (in Chinese). doi: 10.3969/j.issn.1672-8904.2006.04.011 [10] 严鹏, 吴光强. 液力变矩器性能分析[J]. 同济大学学报: 自然科学版, 2004, 32 (11): 1504-1507. doi: 10.3321/j.issn:0253-374X.2004.11.020YAN Peng, WU Guang-qiang. Performance investigation of torque converter[J]. Journal of Tongji University: Natural Science, 2004, 32 (11): 1504-1507. (in Chinese). doi: 10.3321/j.issn:0253-374X.2004.11.020 [11] LEE K H, WOO H, SUK T. Data reduction methods for reverse engineering[J]. The International Journal of Advanced Manufacturing Technology, 2001, 17 (10): 735-743. doi: 10.1007/s001700170119 [12] 刘仕平, 权龙. 三元件向心涡轮液力变矩器环面流线法设计[J]. 农业机械学报, 2009, 40 (7): 20-24. https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX200907006.htmLIU Shi-ping, QUAN Long. Torus streamline method design of3-element centripeta-turbine hydraulic torque converters[J]. Transactions of the Chinese Society of Agricultural Machinery, 2009, 40 (7): 20-24. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX200907006.htm [13] KAMMERER S, MAYER J F, STETTER H, et al. Development of a three-dimensional geometry optimization method for turbomachinery applications[J]. International Journal of Rotating Machinery, 2004, 10 (5): 373-385. doi: 10.1155/S1023621X04000387 -
点击查看大图
图(20) / 表(2)
计量
- 文章访问数: 666
- HTML全文浏览量: 152
- PDF下载量: 683
- 被引次数: 0
