Control law design of dynamic positioning for ship based on dynamic surface control
-
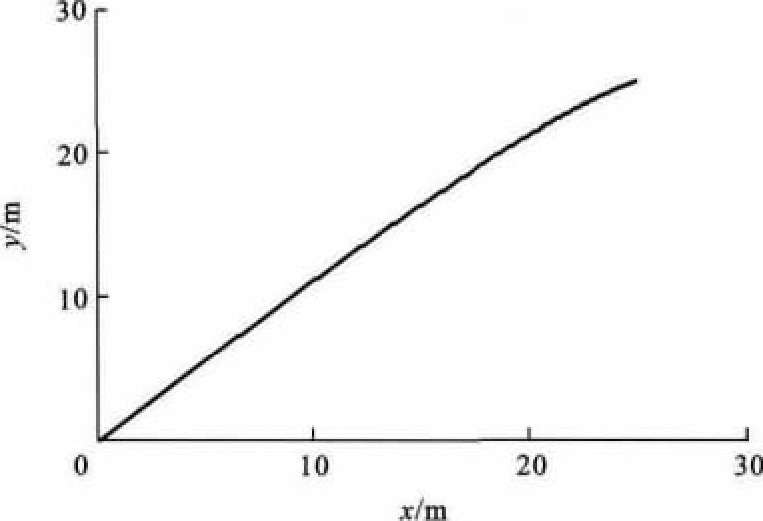
摘要: 针对水面船舶动力定位控制问题, 考虑带有未知界的时变环境扰动, 将动态面控制技术与矢量逆推方法相结合, 设计了船舶动力定位系统的自适应鲁棒非线性控制律。引入动态面控制技术, 利用一阶滤波器的微分项代替虚拟控制矢量的微分项, 使得在控制律设计过程中的微分运算被简单的代数运算所替代, 简化了计算, 易于工程实现。为阻止自适应参数漂移, 采用包含基于σ-修正泄漏项的自适应律估计未知扰动的界。应用Lyapunov函数证明了所设计的控制律能迫使船舶的位置和艏向角达到并保持在期望值, 保证船舶动力定位闭环系统中所有信号最终一致有界。仿真结果表明: 在水平面上, 当船舶初始位置偏离期望位置25m时, 利用设计的控制律能迫使船舶在50s内达到期望的目标位置, 因此, 所设计的控制律是有效的。Abstract: The control problem of dynamic positioning for surface ship was analyzed, the timevariant environmental disturbances with unknown bounds were considered, the dynamic surface control technology was combined with the vectorial backstepping method, based on which, an adaptive robust nonlinear control law of dynamic positioning was proposed.By introducing the dynamic surface control technique, the proposed control law utilized the differentiation term of the first-order low-pass filter to replace the differentiation term of virtual control vector.As a result, the differentiation operations in the control law design were replaced by the simple algebraic operations.Hence, the control law simplified the computation and was implemented in engineering practice easily.Leakage terms based on a variation of σ-modification were incorporated into the adaptive laws for estimating the unknown bounds of disturbances to prevent parameters from drifting.By using the Lyapunov function, it was proved that the proposed control law could force the ship's position and heading to converge and keep at the desired target values and guarantee the uniformly ultimate boundedness of all signals in the closed-loop dynamic positioning system of ship.Simulation result shows that as the initial horizontal-plane position of ship deviates 25 m from the desired position, the ship can achieve the desired position within 50 sbased on the control law, so the proposed control law is effective.
-
0. 引言
根据国际海事组织、挪威船级社等的定义, 船舶动力定位是指船舶利用其自身的推进系统产生的推进力, 来抵御风、浪、流等外界环境干扰的影响, 使船舶以一定姿态自动地保持在海面某一固定位置或精确地跟踪某一预设轨迹[1]。相比传统的锚泊定位, 动力定位操作方便, 避免破坏海床, 定位成本不会随着水深增加而增大, 已经被广泛应用于钻井平台、铺管船舶、供给船舶等[2], 深入开展船舶动力定位技术的研究对海洋资源的开采和利用有着重要的现实意义。
自从20世纪60年代, 动力定位控制技术在商业上被成功应用以来, 比例-微分-积分(PID) 控制和基于卡尔曼滤波与最优控制理论的控制方法等先后被成功应用于动力定位控制系统中[3]。近年来, 随着非线性控制理论的发展, 出现了非线性动力定位控制器, 避免了最优控制器设计过程中需对船舶运动数学模型进行线性化的要求, 得到了全局稳定的结果。Grøvlen等应用逆推设计工具和Lyapunov稳定性理论设计了全局渐近稳定的船舶动力定位控制律[4]; Fossen等通过引进矢量逆推的概念, 简化了船舶动力定位控制律逆推方法[4]设计步骤, 并且得到全局指数稳定的结果[5]; 王元慧等基于非线性模型预测控制技术设计了船舶动力定位控制器, 实现了船舶的动力定位[6]。
但是上述结果在设计过程中均忽略了来自风、浪、流等外部环境扰动的影响, 而这在实践中是非常苛刻的条件。在考虑了恒值的环境扰动及其不确定性条件下, 杜佳璐等基于Luenberger非线性观测器, 采用带有积分作用的逆推方法设计了非线性输出反馈控制律, 应用串级理论证明了系统的全局稳定性[7]; 针对外部扰动为已知恒值和未知恒值2种情况, Muhammad等设计了鲁棒无源输出反馈控制器, 实现船舶动力定位控制的渐近镇定[8]; 在假设环境扰动与船舶参数均为界已知的未知恒值的情况下, Do结合投影算法与逆推方法设计了船舶动力定位鲁棒自适应控制器, 可使船舶位置和艏向角全局渐近收敛于期望值[9]; Fossen等基于无源性理论提出了带有偏的状态估计和海浪滤波的非线性无源观测器, 减少了观测器参数调节的数目[10]; 在无源观测器的基础上, Loria等设计了仅仅依赖于船舶的位置和艏向角的比例微分型全局渐近稳定输出反馈动力定位控制器, 在一艘1∶70的模型船上进行试验, 验证了控制律的有效性[11]; 赵大威等基于自抗扰控制技术, 采用三阶扩张观测器估计出船舶位置、速度和未建模动态, 利用非线性反馈对误差和扰动进行补偿, 设计了船舶动力定位控制器[12], 但是没有给出控制系统的稳定性证明。事实上, 风、浪、流等环境因素时常发生变化, 将海中作业的船舶所遭受的外部环境扰动视为未知时变的扰动更实际, 在没有外界扰动的任何先验知识的情况下, 设计全局稳定的船舶动力定位控制器是一个具有挑战性的工作。
Swaroop等提出了动态面控制方法, 在传统的逆推方法设计过程中引入一阶低通滤波器, 利用一阶滤波器的微分项避免对虚拟控制进行微分, 即在每一步的中间虚拟控制器设计过程中, 用简单的代数运算代替了微分运算, 简化了设计结果的复杂性[13]。受上述研究的启发, 考虑到船舶所遭受的未知时变的外部环境扰动, 本文将动态面控制技术融合到矢量逆推方法中, 设计了船舶动力定位自适应鲁棒控制律。该控制律无需已知外界时变环境扰动的先验知识, 设计自适应律估计未知扰动的界, 且引入动态面控制技术, 消除逆推方法对虚拟控制求导引起的控制律项数膨胀问题, 易于工程实现。应用Lyapunov函数证明该控制律不仅能保证船舶动力定位控制系统的稳定性与定位精度, 而且还能保证闭环系统中所有信号一致最终有界。最后基于一艘动力定位船舶的仿真试验验证了所设计控制律的有效性。
1. 问题描述与预备知识
假设动力定位船舶是左右对称的, 只考虑船舶的前进、横漂和艏向3个自由度的水平面运动, 动力定位船舶的非线性数学模型为[3]
式中: η为船舶位置, 由大地坐标系下的船舶横、纵向位置x、y和艏向角ψ组成; υ为船舶速度, 由随船坐标系下的船舶前进速度u、横漂速度v和艏向角速度r组成; J为大地坐标系和随船坐标系之间的旋转矩阵; M为包含附加矩阵的惯性矩阵, 为可逆的对称正定矩阵; D为线性阻尼矩阵; τ为船舶推进系统提供的控制向量, 由前进控制力τ1、横漂控制力τ2和艏向控制力矩τ3组成; d为风、浪、流等环境因素对船舶综合作用的等效外界干扰力, 由横向干扰力d1、纵向干扰力d2与艏向干扰力矩d3组成。
假设di为时变未知变量, 并满足
式中: pi*为第i个扰动量的未知界。
考虑到海况时常发生变化, 时变的外界环境的能量是有限的, 其对海中作业的船舶产生的干扰力和力矩都是有界的量, 因此, 假设是合理的。
本文的控制目标是考虑船舶遭受完全未知的有界时变环境扰动, 设计自适应鲁棒反馈控制律τ, 使船舶的实际位置(x, y) 和艏向角ψ达到并保持于期望的目标位置ηd, 实现船舶动力定位控制
式中: xd、yd分别为横、纵向目标位置; ψd为目标艏向角。
2. 基于动态面控制的船舶动力定位自适应鲁棒控制律设计
将动态面控制技术与矢量逆推方法相结合, 采用包含基于σ-修正泄漏项的参数自适应律, 设计船舶动力定位自适应鲁棒控制律, 同时分析系统的稳定性。设计过程分为2步。
第1步: 定义动力定位船舶的位置误差面向量S1为
对时间求导, 可得
υ被视为虚拟控制向量, 选择虚拟镇定函数向量φ1为
式中: K1为位置误差的正定对称设计矩阵。
为了避免传统的逆推设计方法的项数爆炸问题, 引进新的状态向量Xd, 并定义如下一阶低通滤波器
式中: T为滤波器时间常数。
第2步: 定义动力定位船舶的速度误差面向量S2为
设计船舶动力定位控制律为
式中: K2为速度误差的正定对称设计矩阵;
定义系统的边界层误差函数向量Y为
考虑式(13)、(7) 和(12), 可得
H (S1, K1, η, υ) 为某一连续函数, 如果
则其在有界区间上的上确界记为N。
选择Lyapunov预选函数V为
式中: P*为扰动量的界向量。
对时间求导, 得
依式(5)、(8) 和(13), 考虑到特性‖J‖=1, 可得
式中: α1、α2为正常数。
依式(9)、(10) 和(2), 考虑假设, 可得
根据式(14)、(15), 可得
式中: α3为正常数。
根据式(11), 有
应用双曲正切函数的性质[14], 对于实数β与ε > 0有
同时考虑下面的不等式
综合式(19) 和(21), 可得
将式(18)、(20)、(24) 代入式(17), 有
式中: λmin (·) 和λmax (·) 分别为矩阵的最小特征值和最大特征值。
根据上述分析, 给出下面的定理。
定理考虑船舶动力定位系统的非线性数学模型式(1)、(2), 在假设的情况下, 带有一阶低通滤波器式(7) 的非线性自适应鲁棒控制律式(10)、(11) 可使船舶的位置(x, y) 和艏向角ψ达到并保持于期望值ηd, 并保证船舶动力定位闭环系统中的所有信号一致最终有界。通过适当地调整设计参数K1、K2、A、F、pi0、εi和滤波器的时间常数T满足式(32) ~ (35), 可以使船舶动力定位达到期望的定位精度。
证明: 解式(25) 可得
式中: V0是V的初值; t为时间。
可见, V是一致最终有界的; 依式(16) 知系统中的信号S1、S2、Y、
根据式(16) 和(36), 可得
可见, 对S1任意的界
3. 仿真结果研究
3.1 控制律验证
以一艘动力定位船为例进行仿真研究, 验证设计控制方法的有效性。该船长175m, 质量为2.460 962×107 kg, 船舶数学模型的参数如下[15]
在仿真中, 设船舶的期望位置为(0, 0, 0)T, 船舶动力定位系统初始状态的η与υ分别为(25 m, 25m, 10°)T与(0, 0, 0)T, 表明船舶在水面的初始位置在x和y方向上均偏离期望值25m, 艏向角偏离10°。扰动界估计
式中: b为大地坐标系下的扰动向量; n为零均值高斯白噪声向量; Tb为时间常数对角阵; ρ为白噪声向量n的幅值矩阵。
图 5 扰动分量绝对值及其界的估计曲线Figure 5. Curves of absolute values of external disturbances and their thresholds' estimation values由图 1~5可见, 在图 4的推进力和力矩作用下, 船舶能够克服外部环境扰动的作用, 在大约50s后达到期望位置并保持在期望的目标位置上, 船舶动力定位闭环系统中所有信号一致最终有界, 正如定理中所述, 从而验证了控制律的有效性。定量的动力定位控制性能指标见表 1。
表 1 控制律的性能指标比较Table 1. Performance index comparison of control laws
3.2 控制性能比较
本文将自适应鲁棒控制律τ与不带扰动界估计的非鲁棒动态面控制律τcmp的动力定位控制性能进行比较
式中: K1cmp与K2cmp分别为非鲁棒动态面控制位置误差与速度误差的正定对称设计矩阵; Tcmp为对应控制的时间常数; Xdcmp为对应控制的状态向量。
在2种不同海况下, 通过仿真对2种控制律的控制结果进行比较, 海况(a) 中船舶遭受与3.1节中相同的时变扰动da, 即da=d, 海况(b) 中船舶遭受较大的时变扰动db, 产生扰动量的马尔科夫过程的白噪声幅值扩大10倍。控制律τcmp的设计参数与控制律τ对应的设计参数取值相同, 即Tcmp、K1cmp与K2cmp分别与T、K1、K2相等。系统的初始条件与3.1节中的相同, 定位性能比较结果见图 6、7, 控制性能见表 1。
由表 1可见, 在2种海况下, 本文所提出的控制律τ的定位误差衰减均相对较快, 定位稳态误差较小, 控制性能均优于τcmp, 且海况越大, 优越性越明显。其原因是本文所提出的自适应鲁棒算法给出了未知扰动界的估计, 控制律τ包含扰动补偿项, 可抑制未知的外部干扰; 相反, 在τcmp控制律中不包含外部扰动的补偿项, 从而导致了较大的定位误差。
4. 结语
考虑到海上工作的动力定位船舶所遭受的外部环境扰动时常发生变化, 本文在假设环境扰动及其界未知的情况下, 将动态面控制技术与矢量逆推设计工具相结合, 设计了船舶动力定位系统的非线性自适应鲁棒控制律。引入动态面控制技术消除了传统逆推方法中固有的计算复杂性问题, 使控制律易于工程实现。在未知扰动界的自适应律中应用基于σ-修正泄漏项, 阻止参数的漂移。借助Lyapunov函数证明了所设计的控制律能够抑制未知的外部环境干扰, 调节船舶的位置和艏向角, 达到并保持期望的目标值, 并保证船舶动力定位闭环系统中所有信号一致最终有界。以一艘动力定位船舶为对象进行了仿真试验, 验证了所提出控制律的有效性。本文所提出的控制律还可应用于船舶的停泊控制等方面。
-
图 5 扰动分量绝对值及其界的估计曲线
Figure 5. Curves of absolute values of external disturbances and their thresholds' estimation values
-
[1] SΦRENSEN A J. A survey of dynamic positioning control systems[J]. Annual Reviews in Control, 2011, 35 (1): 123-136. doi: 10.1016/j.arcontrol.2011.03.008 [2] STRAND J P, SØRENSEN A J, RONSS M, et al. The Ocean Engineering Handbook[M]. Boca Raton: CRC Press, 2001. [3] FOSSEN T I. Marine Control Systems: Guidance, Navigation, and Control of Ships, Rigs, and Underwater Vehicles[M]. Trondheim: Marine Cybernetics, 2002. [4] GRØVLENÅ, FOSSEN T I. Nonlinear control of dynamic positioned ships using only position feedback: an observer backstepping approach[C]//IEEE. Proceedings of the 35th IEEE Conference Decision and Control. Kobe: IEEE, 1996: 3388-3393. [5] FOSSEN T I, GRØVLENÅ. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping[J]. IEEE Transactions on Control Systems Technology, 1998, 6 (1): 121-128. doi: 10.1109/87.654882 [6] 王元慧, 隋玉峰, 吴静. 基于非线性模型预测的船舶动力定位控制器设计[J]. 哈尔滨工程大学学报, 2013, 34 (1): 110-115. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201301019.htmWANG Yuan-hui, SUI Yu-feng, WU Jing. Marine dynamic position system based on nonlinear model predictive control[J]. Journal of Harbin Engineering University, 2013, 34 (1): 110-115. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201301019.htm [7] 杜佳璐, 李文华, 郑凯, 等. 船舶动力定位系统的非线性输出反馈控制[J]. 华南理工大学学报: 自然科学版, 2012, 40 (2): 70-75, 91. doi: 10.3969/j.issn.1000-565X.2012.02.013DU Jia-lu, LI Wen-hua, ZHENG Kai, et al. Nonlinear output feedback control of dynamic positioning system of ships[J]. Journal of South China University of Technology: Natural Science Edition, 2012, 40 (2): 70-75, 91. (in Chinese). doi: 10.3969/j.issn.1000-565X.2012.02.013 [8] MUHAMMAD S, DORIA-CEREZO A. Passivity-based control applied to the dynamic positioning of ships[J]. IET Control Theory and Applications, 2012, 6 (5): 680-688. doi: 10.1049/iet-cta.2010.0554 [9] DO K D. Global robust and adaptive output feedback dynamic positioning of surface ships[J]. Journal of Marine of Science and Application, 2011, 10 (3): 325-332. doi: 10.1007/s11804-011-1076-z [10] FOSSEN T I, STRAND J P. Passive nonlinear observer design for ships using Lyapunov methods: full-scale experiments results with a supply vessel[J]. Automatica, 1999, 35 (1): 3-16. doi: 10.1016/S0005-1098(98)00121-6 [11] LORIA A, FOSSEN T I, PANTELEY E. A separation principle for dynamic positioning of ships: theoretical and experimental results[J]. IEEE Transactions on Control Systems Technology, 2000, 8 (2): 332-343. doi: 10.1109/87.826804 [12] 赵大威, 边信黔, 丁福光. 非线性船舶动力定位控制器设计[J]. 哈尔滨工程大学学报, 2011, 32 (1): 57-61. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201301019.htmZHAO Da-wei, BIAN Xin-qian, DING Fu-guang. Design of a nonlinear controller for dynamic ship positioning[J]. Journal of Harbin Engineering University, 2011, 32 (1): 57-61. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201301019.htm [13] SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45 (10): 1893-1899. [14] POLYCARPOU M M, IOANNOU P A. A robust adaptive nonlinear control design[J]. Automatica, 1996, 32 (3): 423-427. [15] DING Fu-guang, WANG Yuan-hui, TAN Jin-feng. Application of nonlinear filter on the position estimation of dynamic positioned ship[C]//IEEE. Proceedings of the 8th World Congress on Intelligent Control and Automation. Taibei: IEEE, 2011: 1071-1074. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 914
- HTML全文浏览量: 146
- PDF下载量: 807
- 被引次数: 0
