Complexity metric of waterborne traffic flow based on Lempel-Ziv algorithm and TOPSIS
-
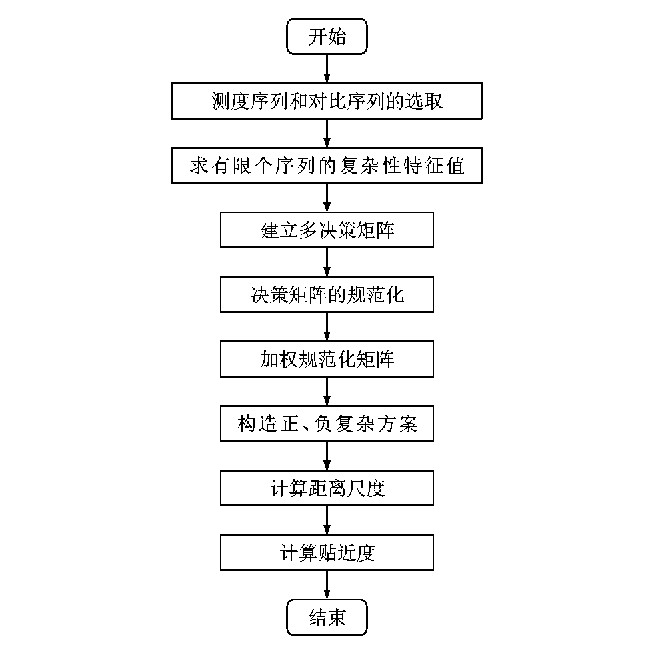
摘要: 为了定量分析并划分水上交通流的复杂性等级, 提出了一种基于Lempel-Ziv算法与TOPSIS的水上交通流复杂性测度方法。运用Lempel-Ziv算法求得实测水上交通流时间序列和对比序列(周期序列、Logistic序列、Henon序列、随机序列) 的复杂性特征值, 采用TOPSIS得到各个序列的贴近度, 根据对比序列的贴近度划分复杂性等级区间, 按照水上交通流时间序列的贴近度和所在的复杂性等级区间来表征各个序列的复杂程度, 并对长江口南槽航道的实测水上交通流进行复杂性测度。计算结果表明: 船舶交通事故数量和下行标准船舶数量与船舶交通流时序复杂性贴近度的相关系数分别为0.698 1、0.769 2, 变化趋势基本一致, 表明贴近度的计算结果可以反映水域船舶交通流的复杂性; 周期序列的贴近度为0.000 1, 随机序列的贴近度为0.999 9, Logistic序列和Henon序列的贴近度分别为0.449 2、0.537 7, 其值大于周期序列的贴近度, 小于随机序列的贴近度; 2013年7~11月水上交通流序列的贴近度分别为0.828 0、0.852 7、0.856 5、0.823 7、0.810 7, 说明序列的复杂性基本一致; 5个月的水上交通流序列的贴近度远大于周期序列的贴近度, 处于随机序列和Henon序列的贴近度之间, 更接近随机序列的贴近度, 说明水上交通流系统不是周期与完全随机的动力学系统; 5个月水上交通流复杂性的整体等级为1级, 表现出高复杂性的特点。
-
关键词:
- 水运工程 /
- 水上交通流 /
- Lempel-Ziv算法 /
- TOPSIS /
- 复杂性等级
Abstract: In order to quantitatively analyze and classify waterborne traffic flow complexity, a method of waterborne traffic flow complexity metric was proposed based on Lempel-Ziv algorithm and TOPSIS (technique for order preference by similarity to an ideal solution).Firstly, LempelZiv algorithm was used to obtain the complexity eigenvalues of measured time sequences ofwaterborne traffic flow and other compared sequences (periodic sequence, logistic sequence, Henon sequence and random sequence).Secondly, the close degree of each sequence was calculated by using TOPSIS.The class of complexity was divided by those close degrees of compared sequences.At last, the complexity degree of each sequence was represented by close degrees of time sequences of waterborne traffic flow and the complexity class.This complexity metric was carried out on the waterborne traffic flow of south channel of the Yangtze River.Calculation result shows that the correlation coefficient of complexity close degree of waterborne ship traffic flow is 0.698 1 with the number of ship traffic accidents, and 0.769 2 with the downside traffic flow of standard ships, respectively.The change trend is basically consistent, so the complexity close degree can reflect the complexity of waterborne ship traffic flow.The close degrees of periodic sequence and random sequence are 0.000 1 and 0.999 9, respectively.Meanwhile, the close degrees of logistic sequence and Henon sequence are 0.449 2 and 0.537 7, respectively.The close degrees of logistic sequence and Henon sequence are greater than periodic sequence and and less than random sequence.The close degrees of waterborne traffic flow from July to November in 2013 are 0.828 0, 0.852 7, 0.856 5, 0.823 7 and 0.810 7, respectively, the complexity of waterborne traffic flow is basically consistent.The values of waterborne traffic flow are far greater than those of periodic sequence, locate between the values of Henon sequence and random sequence, and are closer to the value of random sequence, which shows that the waterborne traffic system is neither periodic nor completely stochastic.The complexity class of time sequence of waterborne traffic flow is Level 1, showing high complexity.-
Key words:
- marine traffic engineering /
- waterborne traffic flow /
- Lempel-Ziv algorithm /
- TOPSIS /
- complexity class
-
图 9 交通事故数量和贴近度的关系
Figure 9. Relationship between number of traffic accidents and close degree
图 10 下行标准船舶数量与贴近度的关系
Figure 10. Relationship between number of downside standard ships and close degree
表 2 实测序列和对比序列的复杂性特征值
Table 2. Complexity eigenvalues of measured sequences and compared sequences
下载: 导出CSV
表 3 时间序列与对比序列的距离尺度及贴近度
Table 3. Distance scales and close degrees of time sequences and compared sequences
下载: 导出CSV
-
[1] 黄亚敏. 水上交通复杂性测度研究[D]. 武汉: 武汉理工大学, 2014.HUANG Ya-min. Study on marine traffic flow complexity metric[D]. Wuhan: Wuhan University of Technology, 2014. (in Chinese). [2] 毛喆, 严新平, 陈辉, 等. 水上交通事故分析研究进展[J]. 中国安全科学学报, 2010, 20 (12): 86-92. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201012017.htmMAO Zhe, YAN Xin-ping, CHEN Hui, et al. Overview on marine accident analysis and its research trends[J]. China Safety Science Journal, 2010, 20 (12): 86-92. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201012017.htm [3] 刘峰涛. 宏微观交通运输系统的复杂性测度及其管控应用[D]. 天津: 天津大学, 2006.LIU Feng-tao. Complexity measure of macroscopical and microcosmic transportation systems and its application to management and control[D]. Tianjin: Tianjin University, 2006. (in Chinese). [4] 朱俊, 张玮. 基于跟驰理论的内河航道通过能力计算模型[J]. 交通运输工程学报, 2009, 9 (5): 83-87. http://transport.chd.edu.cn/article/id/200905015ZHU Jun, ZHANG Wei. Calculation model of inland waterway transit capacity based on ship-following theory[J]. Journal of Traffic and Transportation Engineering, 2009, 9 (5): 83-87. (in Chinese). http://transport.chd.edu.cn/article/id/200905015 [5] 张勇. 交通流的非线性分析、预测和控制[D]. 北京: 北京交通大学, 2011.ZHANG Yong. Nonlinear characteristics analysis, predication and control of traffic flow[D]. Beijing: Beijing Jiaotong University, 2011. (in Chinese). [6] GOERLANDT F, STHLBERG K, KUJALA P. Influence of impact scenario models on collision risk analysis[J]. Ocean Engineering, 2012, 47: 74-87. doi: 10.1016/j.oceaneng.2012.03.006 [7] 徐武雄, 初秀民, 陈先桥, 等. 桥区航道交通流仿真中船舶生成方法[J]. 系统仿真学报, 2014, 26 (8): 1644-1651. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ201408004.htmXU Wu-xiong, CHU Xiu-min, CHEN Xian-qiao, et al. Methods of generating vessels for traffic flow simulation of bridge areas waterway[J]. Journal of System Simulation, 2014, 26 (8): 1644-1651. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ201408004.htm [8] 谭志荣, 严新平, 刘亮. 长江干线桥区船舶到达规律数学模型及检验[J]. 交通信息与安全, 2010, 29 (2): 70-73. https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS201002015.htmTAN Zhi-rong, YAN Xin-ping, LIU Liang. Examination of vessel traffic flow distribution model in Yangtze River Bridge area[J]. Journal of Transport Information and Safety, 2010, 29 (2): 70-73. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS201002015.htm [9] ÖZBAıB, OR I. Analysis and control of maritime transit traffic through the Istanbul Channel: a simulation approach[J]. Central European Journal of Operations Research, 2007, 15 (3): 235-252. https://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ202012011.htm [10] 曹宝贵. 交通流复杂动态特性与交通拥堵问题研究[D]. 长春: 吉林大学, 2010.CAO Bao-gui. The study on complex and dynamic characteristics of traffic flow and traffic jams[D]. Changchun: Jilin University, 2010. (in Chinese). [11] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences, 1991, 88 (6): 2297-2301. doi: 10.1073/pnas.88.6.2297 [12] COOK A, BLOM H A P, LILLO F, et al. Applying complexity science to air traffic management[J]. Journal of Air Transport Management, 2014, 42: 149-158. [13] 刘峰涛. 从意向性到映射: 系统复杂性测度的理论架构[J]. 科学研究, 2009, 27 (7): 968-975. https://www.cnki.com.cn/Article/CJFDTOTAL-KXYJ200907003.htmLIU Feng-tao. From intention to map: theoretical framework of the measure of system complexity[J]. Studies in Science of Science, 2009, 27 (7): 968-975. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KXYJ200907003.htm [14] 徐庚保, 曾莲芝. 基于仿真的复杂系统研究[J]. 计算机仿真, 2013, 30 (2): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201302002.htmXU Geng-bao, ZENG Lian-zhi. Simulation-based complex system study[J]. Computer Simulation, 2013, 30 (2): 1-4. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201302002.htm [15] SHANG Peng-jian, LI Xue-wei, KAMAE S. Nonlinear analysis of traffic time series at different temporal scales[J]. Physics Letters A, 2006, 357 (4/5): 314-318. [16] WEN Yuan-qiao, HUANG Ya-min, ZHOU Chun-hui, et al. Modelling of marine traffic flow complexity[J]. Ocean Engineering, 2015, 104: 500-510. [17] 文元桥, 黄亚敏, 杨君兰, 等. 水上交通流结构复杂度建模[J]. 中国航海, 2014, 37 (2): 62-68. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHH201402015.htmWEN Yuan-qiao, HUANG Ya-min, YANG Jun-lan, et al. Modeling of marine traffic flow structure complexity[J]. Navigation of China, 2014, 37 (2): 62-68. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHH201402015.htm [18] FERMO L, TOSIN A. A fully-discrete-state kinetic theory approach to traffic flow on road networks[J]. Mathematical Models and Methods in Applied Sciences, 2015, 25 (3): 423-461. [19] 叶博嘉, 胡明华, 张晨, 等. 基于交通结构的空中交通复杂性建模[J]. 交通运输系统工程与信息, 2012, 12 (1): 166-172. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201201026.htmYE Bo-jia, HU Ming-hua, ZHANG Chen, et al. Traffic structure-based air traffic complexity modeling[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12 (1): 166-172. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201201026.htm [20] 张勇, 关伟. 基于联合熵和C0复杂度的交通流复杂性测度[J]. 计算机工程与应用, 2010, 46 (15): 22-24, 33. https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201015007.htmZHANG Yong, GUAN Wei. Complexity measure of traffic flow based on union entropy and C0complexity[J]. Computer Engineering and Applications, 2010, 46 (15): 22-24, 33. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201015007.htm [21] AGUARÓN-JOVEN J, ESCOBAR-URMENETA M T, GARCÍAALCARAZ J L, et al. A new synthesis procedure for TOPSIS based on AHP[J]. DYNA, 2015, 82 (191): 11-19. [22] LEMPEL A, ZIV J. On the complexity of finite sequences[J]. IEEE Transactions on Information Theory, 1976, 22 (1): 75-81. [23] 刘峰涛. 城市与高速公路交通流复杂度的测度及比较[J]. 系统工程, 2007, 25 (7): 78-82. https://www.cnki.com.cn/Article/CJFDTOTAL-GCXT200707015.htmLIU Feng-tao. Complexity measures and comparison of urban traffic flow and freeway traffic flow[J]. Systems Engineering, 2007, 25 (7): 78-82. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCXT200707015.htm [24] 谈国强. 离散混沌系统的复杂性算法研究[D]. 长沙: 中南大学, 2007.TAN Guo-qiang. Complexity study of the discrete chaos system[D]. Changsha: Central South University, 2007. (in Chinese). [25] LI Jian, YE Xiang-dong. Recent development of chaos theory in topological dynamics[J]. Acta Mathematica Sinica, English Series, 2016, 32 (1): 83-114. [26] 袁利国. 基于Logistic模型的几类系统的动力学研究及其参数估计[D]. 广州: 华南理工大学, 2012.YUAN Li-guo. Research on dynamics of several dynamical systems based on logistic models and parameter identification[D]. Guangzhou: South China University of Technology, 2012. (in Chinese). [27] AKHMET M U, FEN M O. Entrainment by chaos[J]. Journal of Nonlinear Science, 2014, 24 (3): 411-439. [28] 张蕾. 长江干线典型航道通过能力仿真研究[D]. 武汉: 武汉理工大学, 2009.ZHANG Lei. A simulation approach to typical waterway capacity on the trunk line of the Yangtze River[D]. Wuhan: Wuhan University of Technology, 2009. (in Chinese). [29] LI Jian, YANG Xing, LIU Ke-zhong, et al. Study on the fluency of one-way waterway transportation based on First Come First Served (FCFS) model[C]//IEEE. The 3rd International Conference on Transportation Information and Safety. New York: IEEE, 2015: 669-674. [30] 张勇, 关伟. 采用LS-SVM计算时间序列的Lyapunov指数谱[J]. 计算机工程与应用, 2009, 45 (31): 196-199. https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200931060.htmZHANG Yong, GUAN Wei. Calculation Lyapunov exponent spectrum of time series based on least-squared support vector machine[J]. Computer Engineering and Applications, 2009, 45 (31): 196-199. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200931060.htm [31] 严新平, 张笛, 张明阳, 等. 从ESREL2015国际会议的动态展望交通安全发展[J]. 交通信息与安全, 2015, 33 (5): 1-8, 15. https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS201505001.htmYAN Xin-ping, ZHANG Di, ZHANG Ming-yang, et al. Research trends of transportation safety: identified from ESREL 2015 conference[J]. Journal of Transport Information and Safety, 2015, 33 (5): 1-8, 15. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS201505001.htm -
点击查看大图
图(10) / 表(3)
计量
- 文章访问数: 652
- HTML全文浏览量: 135
- PDF下载量: 533
- 被引次数: 0
