出租汽车出行轨迹网络结构复杂性与空间分异特征

付鑫; 杨宇; 孙皓

出租汽车出行轨迹网络结构复杂性与空间分异特征

付鑫^{1, 2,},
杨宇²,
孙皓³

1.
长安大学经济与管理学院, 陕西西安 710064
2.
中国科学院机构地理科学与资源研究所, 北京 100101
3.
西安建筑科技大学机构土木工程学院, 陕西西安 710055

基金项目:

国家自然科学基金项目 41301130

教育部人文社会科学研究基金项目 12YJCZH051

中央高校基本科研业务费专项资金项目 310823161001

详细信息

作者简介:
付鑫(1982-), 男, 山东日照人, 长安大学讲师, 工学博士, 从事交通网络空间研究

中图分类号: U491.1
计量
- 文章访问数: 911
- HTML全文浏览量: 195
- PDF下载量: 586
- 被引次数: 0
出版历程
- 收稿日期: 2016-11-18
- 刊出日期: 2017-04-25

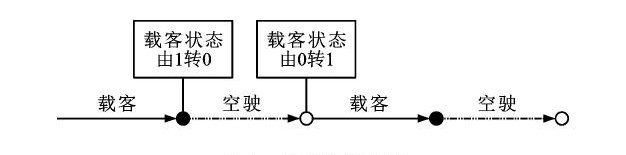
Structural complexity and spatial differentiation characteristics of taxi trip trajectory network

FU Xin^{1, 2
,},
YANG Yu²,
SUN Hao³

1.
School of Economics and Management, Chang'an University, Xi'an 710064, Shaanxi, China
2.
Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
3.
School of Civil Engineering, Xi'an University of Architecture andTechnology, Xi'an 710055, Shaanxi, China

More Information

Author Bio:
FU Xin(1982-), male, lecturer, PhD, +86-29-82334857, fuxin@chd.edu.cn

Article Text (Baidu Translation)

摘要

摘要: 基于出租汽车运行GPS轨迹数据, 构建了一类城市出行复杂网络; 使用有向加权复杂网络测度分析方法, 研究了出租汽车出行轨迹网络结构复杂性与空间分异特征; 以西安市数据为例, 进行了网络指标测算。分析结果表明: 出租汽车出行轨迹网络的平均最短路径长度为2.070 (边数), 聚类系数为0.653, 网络密度为0.554, 说明了该网络是一类典型复杂网络, 具有典型的小世界和集团化特征, 且实际平均出行距离符合对数正态分布; 网络的节点强度均值为411, 最大K-核值为59, 网络中强度小于600的节点占77.97%, 强度小于300的节点占50.24%, 呈现典型的大少小多的空间分布特点; 该网络具有显著的空间分异特征, 重要小区的出行辐射范围具有全局性特征, 总体出行强度空间布局与城市公共交通干线走向一致, 呈十字型分布; 在整个网络范围内, 强中心性交通小区呈现集聚性分布, 重要交通枢纽(车站) 与商圈等区域节点强度大于2 200;出租汽车上下客区域呈现空间非均衡特征, 即在城市重要功能聚集区的上客水平高于下客水平。研究结果反映了出租汽车出行轨迹网络的拓扑结构与空间分异特征间的相互关系, 揭示了城市居民活动的空间特征、活动规律及其与城市功能空间布局之间的相互影响作用。
- 交通工程 /
- 出租汽车 /
- 复杂网络 /
- GPS轨迹数据 /
- 拓扑结构 /
- 空间分异
Abstract: Based on the GPS trajectory data of taxis, a kind of urban trip complex network was constructed.The structural complexity and differentiation characteristics of taxi trip trajectory network were researched by using the directed-weighted complex network measuring method.Based on the taxi trip data of Xi'an, the network indexes were calculated.Analysis result shows that the average shortest path length of taxi trip trajectory network is 2.07 (edge number), the clustering coefficient is 0.653, and the network density is 0.554.So the network is a kind of typical complex network, with typical "small-world"and "collective"characteristic, and the actual average trip distance obeys log-normal distribution.The average value of node strengthsfor the network is 411, the largest K-nuclear value is 59, and the proportions of nodes with the strengths being less than 600 and 300 are 77.97% and 50.24%, respectively, which shows the typical spatial distribution that is described as"less nodes with greater strengths but more nodes with less strengths".The network has significant spatial differentiation characteristic, the traveling radiation scopes of important traffic analysis zones (TAZs) have overall characteristic, the whole spatial layout of trip intensities is consistent with public transport arterial lines, and presents a cross type distribution.The high-level centricity TAZs in whole network present agglomeration distribution, and the node strengths of important transport hubs (stations) and CBD areas are more than 2 200.The distributions of pick-up and drop-off areas of taxis are nonequilibrium, and the pick-up level is higher than the drop-off level in the important functional zones of city.Obviously, this research result indicates the interaction relationship between the topology structure and spatial differentiation of taxi trip trajectory network, and reveals urban resident activities' spatial characteristics, movement rules and the mutual influence of urban functions' spatial layout and resident activities.
- traffic engineering /
- taxi /
- complex network /
- GPS trajectory data /
- topology structure /
- spatial differentiation

HTML全文

由于基层材料的变异性、基层干缩（尤其是水泥基基层）、温度应力、土基压实不够而导致承载力下降和施工接缝，以及施工和养护不当等都会在基层形成裂缝。裂缝在车荷载和环境荷载作用下扩展，继而反射到面层，形成反射裂缝。通常，裂缝方向大致是竖直的，但由于材料的变异性和混合荷载作用下，裂缝也有可能是倾斜的；并且，车荷载与裂缝的相对位置不同，都将车荷载看为Ⅰ型裂缝荷载是很不恰当的，必须对基层混合型裂缝进行深入研究。分析裂缝应力强度因子的方法很多，如有限元、边界元、能量法等，但对于道路特殊的层状结构，权函数方法^[1，2]有独特之处，它不仅精度高，计算简便，而且用权函数分析裂缝的扩展寿命非常简洁，可以减少大量的计算工作。笔者也利用权函数方法对沥青路面Ⅰ型裂缝应力强度因子进行了相应的研究^[3~5]。

1. 基本理论

对于如图 1所示裂缝，在不同荷载作用下，裂缝扩展Δa释放的能量可表示为

${G_1}\Delta a = \frac{1}{H}\left[ {{{\left( {{K_{Ⅰ, 1}}} \right)}^2} + {{\left( {{K_{Ⅱ, 2}}} \right)}^2}} \right]\Delta a = \frac{1}{2}\int_\mathit{\Gamma } {{{\vec t}_1}} \overrightarrow {\Delta {u_1}} {\rm{d}}\mathit{\Gamma }$

(1)

${G_2}\Delta a = \frac{1}{H}\left[ {{{\left( {{K_{Ⅰ, 1}}} \right)}^2} + {{\left( {{K_{Ⅱ, 2}}} \right)}^2}} \right]\Delta a = \frac{1}{2}\int_\mathit{\Gamma } {{{\vec t}_1}} \overrightarrow {\Delta {u_2}} {\rm{d}}\mathit{\Gamma }$

(2)

$H = \left\{ {\begin{array}{*{20}{l}} {E/\left( {1 - {v^2}} \right)}&{平面应变}\\ E&{平面应力} \end{array}} \right.$

(3)

图 1 基层底裂缝

Figure 1. Bottom crack of base layer

下载: 全尺寸图片幻灯片

式中：下标“1”、“2”分别为荷载状态；G为能量释放率；E和v分别为模量和泊松比；$\vec t$和$\overrightarrow {\Delta u} $分别为应力矢量和位移增量矢量。将两种状态叠加得

$\begin{array}{l} \frac{1}{H}\left[ {{{\left( {{K_{Ⅰ, 1}} + {K_{Ⅰ, 2}}} \right)}^2} + {{\left( {{K_{Ⅱ, 1}} + {K_{Ⅱ, 2}}} \right)}^2}} \right]\Delta a = \\ \frac{1}{2}\int_\mathit{\Gamma } {\left[ {{{\vec t}_1}\left( {\overrightarrow {\Delta {u_1}} + \overrightarrow {\Delta {u_2}} } \right) + {{\vec t}_2}\left( {\overrightarrow {\Delta {u_2}} + \overrightarrow {\Delta {u_1}} } \right)} \right]} {\rm{d}}\mathit{\Gamma } \end{array}$

(4)

利用贝蒂互换定理（Betti’s reciprocal theory），即

$\int_\mathit{\Gamma } {{{\vec t}_1}} {\vec u_2}{\rm{d}}\mathit{\Gamma } = \int_\mathit{\Gamma } {{{\vec t}_2}} {\vec u_1}{\rm{d}}\mathit{\Gamma }$

(5)

当裂缝扩展Δa时

$\int_\mathit{\Gamma } {\overrightarrow {{t_1}} } \left( {\overrightarrow {{u_2}} + \overrightarrow {\Delta {u_2}} } \right){\rm{d}}\mathit{\Gamma } = \int_\mathit{\Gamma } {\overrightarrow {{t_2}} } \left( {{{\vec u}_1} + \overrightarrow {\Delta {u_1}} } \right){\rm{d}}\mathit{\Gamma }$

(6)

所以

$\int_\mathit{\Gamma } {\overrightarrow {{t_1}} } \overrightarrow {\Delta {u_2}} {\rm{d}}\mathit{\Gamma } = \int_\mathit{\Gamma } {\overrightarrow {{t_2}} } \overrightarrow {\Delta {u_1}} {\rm{d}}\mathit{\Gamma }$

(7)

${K_{Ⅰ, 1}}{K_{Ⅰ, 2}}{\rm{ + }}{K_{Ⅱ, 1}}{K_{Ⅱ, 2}} = \frac{H}{2}\int_\mathit{\Gamma } {{{\vec t}_1}} \frac{{\overrightarrow {\partial {u_2}} }}{{\partial a}}{\rm{d}}\mathit{\Gamma }$

(8)

由式（8）可知，要得到任意荷载状态下的混合型裂缝应力强度因子，就应该找到两种参考荷载状态，根据上式建立方程组联立求解。下面用两种参考荷载具体表示为

$\begin{array}{l} {K_{Ⅰ}}(a){K_{{\rm{Ⅰ}}, 1}}(a) + {K_{{\rm{Ⅱ}}}}(a){K_{{\rm{Ⅱ}}, 1}}(a) = \\ \;\;\;\;\;\;\frac{H}{2}\int_0^a {\left[ {\sigma (x)\frac{{\partial {v_1}(x, a)}}{{\partial a}} + \tau (x)\frac{{\partial {u_1}(x, a)}}{{\partial a}}} \right]} {\rm{d}}x \end{array}$

(9)

$\begin{array}{l} {K_{Ⅰ}}\left( a \right){K_{Ⅰ, 2}}\left( a \right) + {K_{Ⅱ}}\left( a \right){K_{Ⅱ, 2}}\left( a \right) = \frac{H}{2}\int_0^a {\left[ {\sigma \left( x \right) \cdot } \right.} \\ \left. {\;\;\;\;\;\;\;\;\frac{{\partial {v_2}(x, a)}}{{\partial a}} + \tau (x)\frac{{\partial {u_2}(x, a)}}{{\partial a}}} \right]{\rm{d}}x \end{array}$

(10)

$\begin{array}{l} {K_{Ⅰ}}(a) = \frac{H}{{2D(a)}}\left\{ {\int_0^a {\left[ {{K_{Ⅱ, 2}}(a)\frac{{\partial {v_1}(x, a)}}{{\partial a}} - } \right.} } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {K_{Ⅱ, 1}^{(1)}(a)\frac{{\partial {v_2}(x, a)}}{{\partial a}}} \right]\sigma (x){\rm{d}}x + \int_0^a {\left[ {{K_{Ⅱ, 2}}(a) \cdot } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\frac{{\partial {u_1}(x, a)}}{{\partial a}} - {K_{Ⅱ, 1}}(a)\frac{{\partial {u_2}(x, a)}}{{\partial a}}} \right]\tau (x){\rm{d}}x} \right\} \end{array}$

(11)

$\begin{array}{l} {K_{Ⅱ}}(a) = \frac{H}{{2D(a)}}\left\{ {\int_0^a {\left[ {{K_{Ⅰ, 2}}(a)\frac{{\partial {v_2}(x, a)}}{{\partial a}} - } \right.} } \right.\\ \left. {\;\;\;\;\;\;\;\;\;{K_{Ⅰ, 2}}(a)\frac{{\partial {v_1}(x, a)}}{{\partial a}}} \right]\sigma (x){\rm{d}}x + \int_0^a {\left[ {{K_{Ⅰ, 1}}(a) \cdot } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\left. {\frac{{\partial {u_2}(x, a)}}{{\partial a}} - {K_{Ⅰ, 2}}(a)\frac{{\partial {u_1}(x, a)}}{{\partial a}}} \right]\tau (x){\rm{d}}x} \right\} \end{array}$

(12)

$D(a) = {K_{Ⅰ, 1}}(a){K_{Ⅱ, 2}}(a) - {K_{Ⅱ, 1}}(a){K_{Ⅰ, 2}}(a)$

(13)

只要D（a）≠0，上述方程组才有唯一解。

同样可利用权函数的基本理论^[1~6]，将上述公式用矩阵表示如下

$\left( {\begin{array}{*{20}{l}} {{K_{Ⅰ}}(a)}\\ {{K_{Ⅱ}}(a)} \end{array}} \right) = \int_0^a {\left( {\begin{array}{*{20}{l}} {{h_{Ⅰ\sigma }}(x, a)}&{{h_{Ⅰ\tau }}(x, a)}\\ {{h_{Ⅱ\sigma }}(x, a)}&{{h_{Ⅱ\tau }}(x, a)} \end{array}} \right)} \left( {\begin{array}{*{20}{l}} {\sigma (x)}\\ {\tau (x)} \end{array}} \right){\rm{d}}x$

(14)

权函数用矩阵表示为

$\begin{array}{l} \left( {\begin{array}{*{20}{l}} {{h_{Ⅰ\sigma }}(x, a)}&{{h_{Ⅰ\tau }}(x, a)}\\ {{h_{Ⅱ\sigma }}(x, a)}&{{h_{Ⅱ\tau }}(x, a)} \end{array}} \right) = \frac{H}{{2D(a)}} \cdot \\ \left( {\begin{array}{*{20}{l}} {{K_{Ⅱ, 2}}(a)\frac{{\partial {v_1}(x, a)}}{{\partial a}} - {K_{Ⅱ, 1}}(a)\frac{{\partial {v_2}(x, a)}}{{\partial a}}{K_{Ⅱ, 2}}(a)\frac{{\partial {u_1}(x, a)}}{{\partial a}} - {K_{Ⅱ, 1}}(a)\frac{{\partial {u_2}(x, a)}}{{\partial a}}}\\ {{K_{Ⅰ, 1}}(a)\frac{{\partial {v_2}(x, a)}}{{\partial a}} - {K_{Ⅰ, 2}}(a)\frac{{\partial {v_1}(x, a)}}{{\partial a}}{K_{Ⅰ, 1}}(a)\frac{{\partial {u_2}(x, a)}}{{\partial a}} - {K_{Ⅰ, 2}}(a)\frac{{\partial {u_1}(x, a)}}{{\partial a}}} \end{array}} \right) \end{array}$

(15)

若仅考虑Ⅰ型裂缝，由式（9）或式（10）便可得到Ⅰ型应力强度因子公式

$K = \int_0^a \sigma (x)h(a, x){\rm{d}}x$

(16)

$h(a, x) = \frac{H}{{{K_{Ⅰ, i}}}}\frac{{\partial {v_i}(a, x)}}{{\partial a}}$

(17)

Petroski H J、Achenbach J D在分析Ⅰ型裂缝应力强度因子时，即将William关于裂缝尖端位移的序列级数^[7]近似表达为

$\begin{array}{l} u(a, x) = \frac{{{\sigma _0}}}{{H\sqrt 2 }}\left[ {4F(a){a^{1/2}}{{(a - x)}^{1/2}} + } \right.\\ \left. {G(a){a^{ - 1/2}}{{(a - x)}^{3/2}}} \right] \end{array}$

(18)

所以

$\begin{array}{l} \frac{{\partial u(a, x)}}{{\partial a}} = \frac{{{\sigma _0}}}{{\sqrt 2 H}}\left\{ {2\sqrt a F(a){{(a - x)}^{ - 1/2}} + } \right.\\ \;\;\;\;\;\;\;\;\;\left[ {4\frac{{\partial F(a)}}{{\partial a}}\sqrt a + \frac{{2F(a)}}{{\sqrt a }} + \frac{{3G(a)}}{{2\sqrt a }}} \right]{\rm{. }}\\ \;\;\;\;\;\;\;\;\;{(a - x)^{1/2}} + \left[ {\frac{{\partial G(a)}}{{\partial a}}\frac{1}{{\sqrt a }} - \frac{{G(a)}}{{2{a^{3/2}}}}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\left. {{{(a - x)}^{3/2}}} \right\} \end{array}$

(19)

再对裂缝长度a微分后，代入式（17），上述权函数实际上近似表达为

$\begin{array}{l} h(a, x) = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \left[ {{D_0}{{(1 - \rho )}^{ - 1/2}} + {D_1}{{(1 - \rho )}^{1/2}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{D_2}{{(1 - \rho )}^{3/2}}} \right] \end{array}$

(20)

式中：ρ＝x/a，x轴以裂缝嘴为原点，方向沿裂缝线方向；系数D₀、D₁和D₂是关于裂缝长度a的常数。其实，Petroski H J和Achenbach J D只取了William裂缝尖端位移的序列系数的前两项来近似表示裂缝的实际位移。由于只取了两项，估计会在一些特殊情况产生误差，所以将权函数用无穷级数表示会更精确，如式（21）所示

$h(a, x) = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_n}} {(1 - \rho )^{(n - 1)/2}}$

(21)

同理，也可将混合型权函数用无穷级数表示为

${h_{Ⅰ\sigma }} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅰ\sigma , n}}} {(1 - \rho )^{(n - 1)/2}}$

(22)

${h_{Ⅱ\sigma }} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅱ\sigma , n}}} {(1 - \rho )^{(n - 1)/2}}$

(23)

${h_{Ⅰ\tau }} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅰ\tau , n}}} {(1 - \rho )^{(n - 1)/2}}$

(24)

${h_{Ⅱ\tau }} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅱ\tau , n}}} {(1 - \rho )^{(n - 1)/2}}$

(25)

当然，实际应用不可能取无数项，为此，本文取前面四项进行分析，并且可以证明

$\left\{ {\begin{array}{*{20}{l}} {{D_{Ⅰ\sigma }} = {D_{Ⅱ\tau }} = 1}\\ {{D_{Ⅱ\sigma }} = {D_{Ⅰ\tau }} = 0} \end{array}, (n = 0)} \right.$

(26)

如图 1裂缝，在距裂缝尖点ε（ε/a→0）作用有一对垂直裂缝的单位集中力P，因此应力强度因子可应用无限长裂缝计算公式计算，并且可不考虑几何不对称对应力强度因子的影响，所以这对法向集中力产生的应力强度因子为

${K_{Ⅰ}} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}\varepsilon }}} P, {K_{Ⅱ}} = 0$

(27)

$\sigma (x) = P\delta \left( {x - {x_0}} \right), \tau (x) = 0, \delta (z) = \left\{ {\begin{array}{*{20}{l}} 1&{(z = 0)}\\ 0&{(z \ne 0)} \end{array}} \right.$

(28)

所以

$\left. {\begin{array}{*{20}{l}} {{K_{Ⅰ\sigma }} = \int_0^a \sigma (x){h_{Ⅰ\sigma }}(x, a){\rm{d}}x = }\\ {\;\;\;\;\;\;\;{P_{Ⅰ\sigma }}\left( {{x_0}, a} \right) = {h_{Ⅰ\sigma }}\left( {{x_0}, a} \right)}\\ {\;\;\;\;\;\;\;{K_{Ⅱ\sigma }} = {h_{Ⅱ\sigma }}\left( {{x_0}, a} \right) = 0} \end{array}} \right\}$

(29)

将式（29）代入式（22）、（23），由于（ε/a→0），所以

$\left. {\begin{array}{*{20}{l}} {\sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} {D_{Ⅰ\sigma , 0}}{{\left( {\frac{\varepsilon }{a}} \right)}^{ - 1/2}} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}\varepsilon }}} }\\ {\sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} {D_{Ⅱ\sigma , 0}}{{\left( {\frac{\varepsilon }{a}} \right)}^{ - 1/2}} = 0} \end{array}} \right\}$

(30)

所以

${D_{Ⅰ\sigma }} = 1, {D_{Ⅱ\sigma }} = 0$

(31)

同理，在靠近裂缝尖端作用一对裂缝切向集中力Q，即

$\tau (x) = Q\delta \left( {x - {x_0}} \right)$

(32)

可以得到D_Ⅱτ，0＝1，D_Ⅰτ，0＝0。

为了求出其它未知权函数系数，可在裂缝面上不同位置作用单位法向集中力和单位切向集中力，将法向集中力和切向集中力按照式（28）和（32）用δ函数表示，再代入式（14）和（22~25），可得到

$\left. {\begin{array}{*{20}{l}} {{K_{Ⅰ\sigma }} = {h_{Ⅰ\sigma }}(x, a) = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅰ\sigma , n}}} {{(1 - \rho )}^{(n - 1)/2}}}\\ {{K_{Ⅱ\sigma }} = {h_{Ⅱ\sigma }}(x, a) = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅱ\sigma , n}}} {{(1 - \rho )}^{(n - 1)/2}}}\\ {{K_{Ⅰ\tau }} = {h_{Ⅰ\tau }}(x, a) = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅰ\tau , n}}} {{(1 - \rho )}^{(n - 1)/2}}}\\ {{K_{Ⅱ\tau }} = {h_{Ⅱ\tau }}(x, a) = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}a}}} \sum\limits_{n = 0}^\infty {{D_{Ⅱ\tau , n}}} {{(1 - \rho )}^{(n - 1)/2}}} \end{array}} \right\}$

(33)

由于未知权函数系数为三个，总共12个未知系数，所以只需要三对单位法向集中力和三对单位切向集中力。只要能得到这些集中力的应力强度因子，便可联立方程组求出权函数系数。

2. 有限元方法

从公式（33）可得，只要能计算出任意位置的集中力作用下的应力强度因子，便可以联立方程组得到矩阵权函数余下的系数。为此，下面应用有限元方法来进行辅助分析。

同前文^[5]一样，裂缝尖端单元采用单参八节点变异单元，如图 2、3所示，有限元计算混合型应力强度因子公式为^[8~12]

$\left. {\begin{array}{*{20}{l}} {{K_{Ⅰ}} = \frac{{2\mu }}{{\kappa + 1}}\sqrt {\frac{{2{\rm{ \mathsf{ π} }}}}{l}} \left( {{{\left. {4{U_\theta }} \right|}_B} - {{\left. {{U_\theta }} \right|}_C}} \right)}\\ {{K_{Ⅱ}} = \frac{{2\mu }}{{\kappa + 1}}\sqrt {\frac{{2{\rm{ \mathsf{ π} }}}}{l}} \left( {{{\left. {4{U_r}} \right|}_B} - {{\left. {{U_r}} \right|}_C}} \right)} \end{array}} \right\}$

(34)

图 2 裂缝尖端单元

Figure 2. Elements of crack tip

下载: 全尺寸图片幻灯片

图 3 裂缝尖端面节点

Figure 3. Nodes of crack face

下载: 全尺寸图片幻灯片

式中：U_θ和U_r为垂直裂缝面和沿裂缝面的位移。这里所需要特别强调一点是，在计算U_θ和U_r时，一定要扣除裂缝尖端节点的位移。

三对集中力位置选在ρ＝0、0.4和0.8。利用有限元计算出各单元的节点位移，再转化为裂缝法向和切向位移，代入式（34）可得各集中力产生的混合型应力强度因子K_Ⅰ和K_Ⅱ。为了减少误差，分别计算裂缝上下面的应力强度因子，再取平均值，即

$\left. {\begin{array}{*{20}{l}} {{K_{Ⅰ}} = \left( {{K_{Ⅰ, {\rm{ upper }}}} + {K_{Ⅰ, {\rm{ down }}}}} \right)/2}\\ {{K_{Ⅱ}} = \left( {{K_{Ⅱ, {\rm{ upper }}}} + {K_{Ⅱ, {\rm{ down }}}}} \right)/2} \end{array}} \right\}$

(35)

应力强度因子结果如表 1所示。沥青和基层厚度分别为15 cm和30 cm，模量分别为2000、15000 MPa，土基模量为35 MPa。三层的泊松比分别为0.25、0.25和0.35。裂缝长度为12 cm，角度为75°。整个路面简化为平面应力计算。

表 1 有限元计算的混合型应力强度因子（MPa·cm^1/2 ）

Table 1. Mixed-mode SIFs by finite element method

下载: 导出CSV

| 显示表格

将计算的应力强度因子代入公式，联立求解方程组（33）可得到权函数系数矩阵，如表 2所示。权函数如图 4所示。

表 2 混合型权函数系数

Table 2. Coefficients of mixed┐mode weight function

下载: 导出CSV

| 显示表格

图 4 权函数示意图

Figure 4. Weight functions for base’s bottom crack

下载: 全尺寸图片幻灯片

3. 检验权函数系数

尽管得到了权函数，但是否可行，还需要进一步检验，下面利用公式（33）对所得到的权函数进行检验。为此，本文对三种荷载条件进行了分析，即在裂缝面上作用均匀的法向单位应力、切向单位应力和法向单位应力与切向单位应力组合作用，分别简称Load₁、Load₂和Load₃。利用权函数计算应力强度因子可参照文献[1]的方法。应力强度因子计算结果如表 3所示。

表 3 有限元和权函数方法的应力强度因子计算结果（MPa·cm^1/2）

Table 3. SIF results by finite element method and weight function method

下载: 导出CSV

| 显示表格

4. 结语

从裂缝扩展的能量释放原理、叠加原理和贝蒂互换定理以及William关于裂缝尖端的位移级数序列推导出了混合型裂缝的权函数计算方法，并利用简单的荷载形式，即单位集中力作用下的应力强度因子建立联立方程组，计算出了混合型裂缝的矩阵权函数。并分析了长度为12 cm，角度为75°的基层底裂缝的权函数和应力强度因子。与有限元方法对比分析，该方法得到的权函数计算的混合型应力强度因子计算结果和有限元方法吻合得非常好，说明该方法可行。由于该方法简单，对于分析反射裂缝的扩展很有好处，非常适合工程应用。所有过程都编制了相应的程序来实现，可直接应用于工程实践。

图 1 轨迹数据描述

Figure 1. Description of trajectory data

下载: 全尺寸图片幻灯片

图 2 西安市空间基本形态与交通小区划分

Figure 2. Basic spatial form and TAZ division of Xi'an

下载: 全尺寸图片幻灯片

图 3 西安市出租汽车轨迹复杂网络

Figure 3. Taxi trajectory complex network of Xi'an

下载: 全尺寸图片幻灯片

图 4 各出行小区平均最短路径频次分布

Figure 4. Each travel zone's average shortest path frequency distribution

下载: 全尺寸图片幻灯片

图 5 实际出行距离频次分布

Figure 5. Actual travel distance frequency distribution

下载: 全尺寸图片幻灯片

图 6 西安市出租汽车复杂网络节点强度分布

Figure 6. Node strength distribution of Xi'an's taxi complex network

下载: 全尺寸图片幻灯片

图 7 节点强度排名前11位与后10位的交通小区

Figure 7. Traffic zones having top 11and last 10node strengths

下载: 全尺寸图片幻灯片

图 8 节点强度前4位交通小区OD分布

Figure 8. Traffic zones'OD distribution having top 4node strength

下载: 全尺寸图片幻灯片

图 9 西安市出租汽车复杂网络节点强度等级分布

Figure 9. Node strength grade distribution of Xi'an's taxi complex network

下载: 全尺寸图片幻灯片

图 11 出租汽车出行上客点分布

Figure 11. Pick-up point distribution of taxi trip

下载: 全尺寸图片幻灯片

图 10 节点K-核等级空间分布

Figure 10. Spatial distribution of K-core grades

下载: 全尺寸图片幻灯片

图 12 出租汽车出行下客点分布

Figure 12. Drop-off point distribution of taxi trip

下载: 全尺寸图片幻灯片

表 1 出租汽车GPS轨迹数据基本结构

Table 1. Basic structure of taxi GPS trajectory data

下载: 导出CSV

表 2 网络评价指标计算结果

Table 2. Calculation result of network evaluation indexes

下载: 导出CSV

参考文献(31)

[1]	TANG Jin-jun, JIANG Han, LI Zhi-bin, et al. A two-layer model for taxi customer searching behaviors using GPS trajectory data[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17 (11): 3318-3324. doi: 10.1109/TITS.2016.2544140
[2]	焦龙, 刘岳峰, 司若辰. 距离约束在出租车客流网络结构中的作用研究[J]. 北京大学学报: 自然科学版, 2014, 50 (5): 880-886. https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201405012.htm JIAO Long, LIU Yue-feng, SI Ruo-chen. Role of distance constraint in the structure of taxi passenger flow network[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50 (5): 880-886. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201405012.htm
[3]	周静一, 李晔. 基于浮动车技术的杭州市出租汽车运行特征分析[J]. 科技信息, 2011 (3): 120-122. https://www.cnki.com.cn/Article/CJFDTOTAL-KJXX201103084.htm ZHOU Jing-yi, LI Ye. Operation characteristics analysis of Hangzhou taxis based on floating car technology[J]. Science and Technology Information, 2011 (3): 120-122. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KJXX201103084.htm
[4]	辛飞飞, 陈小鸿, 林航飞. 浮动车数据路网时空分布特征研究[J]. 中国公路学报, 2008, 21 (4): 105-110. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200804017.htm XIN Fei-fei, CHEN Xiao-hong, LIN Hang-fei. Research on time space distribution characteristics of floating car data in road network[J]. China Journal of Highway and Transport, 2008, 21 (4): 105-110. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200804017.htm
[5]	袁长伟, 米雪玉, 吴群琪, 等. 交通拥堵环境下的城市出租车候时费优化模型[J]. 交通运输工程学报, 2014, 14 (2): 75-81. doi: 10.3969/j.issn.1671-1637.2014.02.013 YUAN Chang-wei, MI Xue-yu, WU Qun-qi, et al. Optimal model of taxi waiting time fee under traffic congestion condition[J]. Journal of Traffic and Transportation Engineering, 2014, 14 (2): 75-81. (in Chinese). doi: 10.3969/j.issn.1671-1637.2014.02.013
[6]	COMERT G. Effect of stop line detection in queue length estimation at traffic signals from probe vehicles data[J]. European Journal of Operational Research, 2013, 226 (1): 67-76. doi: 10.1016/j.ejor.2012.10.035
[7]	SUN Jian, ZHANG Chun, ZHANG Li-hui, et al. Urban travel behavior analyses and route prediction based on floating car data[J]. Transportation Letters: the International Journal of Transportation Research, 2014, 6 (3): 118-125.
[8]	俞春辉, 杨晓光, 马万经. 考虑随机需求的出租车上客区泊位设置模式和规模优化方法[J]. 中国公路学报, 2015, 28 (3): 102-109. doi: 10.3969/j.issn.1001-7372.2015.03.014 YU Chun-hui, YANG Xiao-guang, MA Wan-jing. Optimization method for management mode and scale of taxi pick-up zone with stochastic demand[J]. China Journal of Highway and Transport, 2015, 28 (3): 102-109. (in Chinese). doi: 10.3969/j.issn.1001-7372.2015.03.014
[9]	杨英俊, 赵祥模. 基于出租车运行信息的城市出租车运量投放计划模型[J]. 中国公路学报, 2012, 25 (5): 120-125. doi: 10.3969/j.issn.1001-7372.2012.05.019 YANG Ying-jun, ZHAO Xiang-mo. Schedule model of urban taxi quantity based on taxi running information[J]. China Journal of Highway and Transport, 2012, 25 (5): 120-125. (in Chinese). doi: 10.3969/j.issn.1001-7372.2012.05.019
[10]	TANG Jin-jun, LIU Fang, WANG Yin-hai, et al. Uncovering urban human mobility from large scale taxi GPS data[J]. Physica A: Statistical Mechanics and its Applications, 2015, 438: 140-153. doi: 10.1016/j.physa.2015.06.032
[11]	ZHOU Zuo-jian, DOU Wan-chun, JIA Guo-chao, et al. A method for real-time trajectory monitoring to improve taxi service using GPS big data[J]. Information and Management, 2016, 53 (8): 964-977. doi: 10.1016/j.im.2016.04.004
[12]	ZHAO Shuang-ming, ZHAO Peng-xiang, CUI Yun-fan. A network centrality measure framework for analyzing urban traffic flow: a case study of Wuhan, China[J]. Physica A: Statistical Mechanics and its Applications, 2017, 478: 143-157. doi: 10.1016/j.physa.2017.02.069
[13]	刘岳峰, 司若辰, 康葳. 城市出租车客流网络结构复杂性特征研究[J]. 北京大学学报: 自然科学版, 2014, 50 (5): 873-879. https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201405011.htm LIU Yue-feng, SI Ruo-chen, KANG Wei. Complex structural properties of urban taxi passenger flow network[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50 (5): 873-879. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201405011.htm
[14]	CUI Jian-xun, LIU Feng, JANSSENS D, et al. Detecting urban road network accessibility problems using taxi GPS data[J]. Journal of Transport Geography, 2016, 51: 147-157. doi: 10.1016/j.jtrangeo.2015.12.007
[15]	周江评, 陈晓键, 黄伟, 等. 中国中西部大城市的职住平衡与通勤效率——以西安为例[J]. 地理学报, 2013, 68 (10): 1316-1330. doi: 10.11821/dlxb201310002 ZHOU Jiang-ping, CHEN Xiao-jian, HUANG Wei, et al. Jobs-housing balance and commute efficiency in cities of central and western China: a case study of Xi'an[J]. Acta Geographica Sinica, 2013, 68 (10): 1316-1330. (in Chinese). doi: 10.11821/dlxb201310002
[16]	SEATON K A, HACKETT L M. Station, trains and smallworld networks[J]. Physical A: Statistical Mechanics and its Applications, 2004, 339 (3/4): 635-644.
[17]	孙健, 张颖, 张纯. 基于驾驶人路径选择偏好的OD行程时间预测方法[J]. 交通运输工程学报, 2016, 16 (2): 143-149. http://transport.chd.edu.cn/article/id/201602017 SUN Jian, ZHANG Ying, ZHANG Chun. Prediction method of OD travel time based on driver's route choice preference[J]. Journal of Traffic and Transportation Engineering, 2016, 16 (2): 143-149. (in Chinese). http://transport.chd.edu.cn/article/id/201602017
[18]	柯文前. 高速公路交通流网络的时空特征与城市空间关联研究——以江苏省为例[D]. 南京: 南京师范大学, 2015. KE Wen-qian. Spatio-temporal characteristics of expressway traffic flow network and urban spatial interaction: a case study in Jiangsu Province[D]. Nanjing: Nanjing Normal University, 2015. (in Chinese).
[19]	赵月, 杜文, 陈爽. 复杂网络理论在城市交通网络分析中的应用[J]. 城市交通, 2009, 7 (1): 57-65. https://www.cnki.com.cn/Article/CJFDTOTAL-CSJT200901012.htm ZHAO Yue, DU Wen, CHEN Shuang. Application of complex network theory to urban transportation network analysis[J]. Urban Transport of China, 2009, 7 (1): 57-65. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CSJT200901012.htm
[20]	KHLER E, MHRING R H, SKUTELLA M. Traffic networks and flows over time[C]∥Springer. Lecture Notes in Computer Science. Berlin: Springer, 2009: 166-196.
[21]	SUN Jian, GUAN Shi-tuo. Measuring vulnerability of urban metro network from line operation perspective[J]. Transportation Research Part A: Policy and Practice, 2016, 94: 348-359. doi: 10.1016/j.tra.2016.09.024
[22]	罗飞, 魏开平, 万润泽. 复杂网络中最短路径算法的研究及应用[J]. 电子测量技术, 2007, 30 (4): 169-171, 197. https://www.cnki.com.cn/Article/CJFDTOTAL-DZCL200704049.htm LUO Fei, WEI Kai-ping, WAN Run-ze. Research on algorithm for detecting shortest path in complex network and its application[J]. Electronic Measurement Technology, 2007, 30 (4): 169-171, 197. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DZCL200704049.htm
[23]	王林, 张婧婧. 复杂网络的中心化[J]. 复杂系统与复杂性科学, 2006, 3 (1): 13-20. https://www.cnki.com.cn/Article/CJFDTOTAL-FZXT200601001.htm WANG Lin, ZHANG Jing-jing. Centralization of complex networks[J]. Complex Systems and Complexity Science, 2006, 3 (1): 13-20. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FZXT200601001.htm
[24]	JIANG Jiao-jiao, WEN Sheng, YU Shui, et al. The structure of communities in scale-free networks[J]. Concurrency and Computation: Practice and Experience, 2016, DOI: 10.1002/cpe.4040.
[25]	NIE Ting-yuan, GUO Zheng, ZHAO Kun, et al. Using mapping entropy to identify node centrality in complex networks[J]. Physical A: Statistical Mechanics and its Applications, 2016, 453: 290-297.
[26]	OULDISMAIL A A O, AMOUZANDEH G, GRANT S C. Structural connectivity within neural ganglia: a default smallworld network[J]. Neuroscience, 2016, 337: 276-284.
[27]	胡君辉, 徐新平, 杨永栩. 三组城市公共汽车运输网的小世界性质[J]. 广西师范大学学报: 自然科学版, 2006, 24 (2): 10-14. https://www.cnki.com.cn/Article/CJFDTOTAL-GXSF200602002.htm HU Jun-hui, XU Xin-ping, YANG Yong-xu. Small-world properties of 3bus-transport networks of China[J]. Journal of Guangxi Normal University: Natural Science Edition, 2006, 24 (2): 10-14. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXSF200602002.htm
[28]	GHOSHAL G, BARABSI A L. Ranking stability and superstable nodes in complex networks[J]. Nature Communications, 2011, DOI: 10.1038/ncomms1396.
[29]	PARK J, BARABSI A L. Distribution of node characteristics in complex networks[J]. Nature Communications, 2007, 104 (46): 17916-19720.
[30]	LIU Jun, XIONG Qing-yu, SHI Wei-ren, et al. Evaluating the importance of nodes in complex networks[J]. Physical A: Statistical Mechanics and its Applications, 2016, 452: 209-219.
[31]	林强, 曹小曙. 广州城市社区交通特征空间分异研究[J]. 现代城市研究, 2008 (4): 74-82. https://www.cnki.com.cn/Article/CJFDTOTAL-XDCS200804010.htm LIN Qiang, CAO Xiao-shu. Research on characteristic differentiation of urban community transport in Guangzhou[J]. Modern Urban Research, 2008 (4): 74-82. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XDCS200804010.htm

施引文献

资源附件(0)

访问统计

点击查看大图

图(12) / 表(2)

计量

文章访问数: 911
HTML全文浏览量: 195
PDF下载量: 586
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

出租汽车出行轨迹网络结构复杂性与空间分异特征

作者简介:
付鑫(1982-), 男, 山东日照人, 长安大学讲师, 工学博士, 从事交通网络空间研究

计量