全站仪RDM法与3D量测法量测隧道变形精度对比

罗彦斌; 陈建勋; 翟宇辉

全站仪RDM法与3D量测法量测隧道变形精度对比

罗彦斌^{1, 2,},
陈建勋¹,
翟宇辉^{1, 3}

1.
长安大学陕西省公路桥梁与隧道重点实验室, 陕西西安 710064
2.
亚利桑那大学土木工程与工程力学系, 亚利桑那图森 85721
3.
广东省南粤交通投资建设有限公司清云高速公路管理中心, 广东广州 510101

基金项目:

国家自然科学基金项目国家自然科学基金项目

国家自然科学基金项目 51678063

中国博士后科学基金项目 2016M602738

陕西省科技统筹创新工程计划项目 2014KTCG01-02

详细信息

作者简介:
罗彦斌(1980-), 男, 宝鸡千阳人, 长安大学副教授, 工学博士, 从事隧道工程研究

中图分类号: U452.1
计量
- 文章访问数: 784
- HTML全文浏览量: 154
- PDF下载量: 536
- 被引次数: 0
出版历程
- 收稿日期: 2017-03-04
- 刊出日期: 2017-06-25

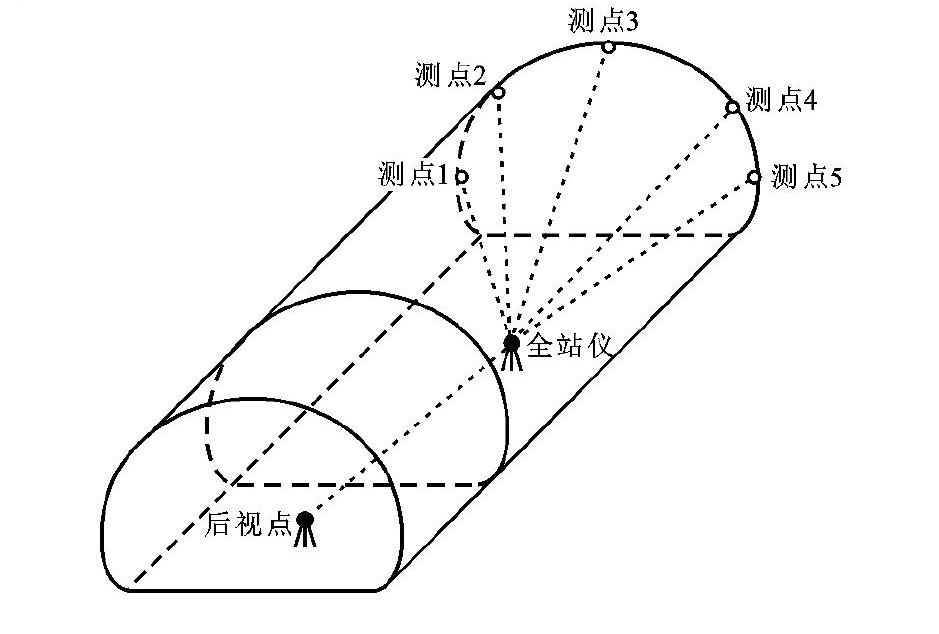
Comparison of measuring accuracies of tunnel displacements with RDM method and 3D measurement method based on total station

LUO Yan-bin^{1, 2
,},
CHEN Jian-xun¹,
ZHAI Yu-hui^{1, 3}

1.
Shaanxi Provincial Major Laboratory for Highway Bridge and Tunnel, Chang'an University, Xi'an 710064, Shaanxi, China
2.
Department of Civil Engineering and Engineering Mechanics, University of Arizona, Tucson 85721, Arizona, USA
3.
Qingyun Expressway Management Center, Guangdong Nanyue Transportation Investment and Construction Co., Ltd., Guangzhou 510101, Guangdong, China

More Information

Author Bio:
LUO Yan-bin(1980-), male, associate professor, PhD, +86-29-82334887, lyb@chd.edu.cn

Article Text (Baidu Translation)

摘要

摘要: 根据测量学原理和误差传播定律, 分析了全站仪自由设站对边量测(RDM) 法和三维坐标(3D) 量测法, 建立了2种量测法的隧道变形精度分析模型, 利用中误差评价隧道变形量测精度, 推导了2种方法量测隧道变形的中误差计算公式, 并以某三车道公路隧道为例, 对2种方法的量测精度进行了对比和验证; RDM法通过三角高程测量原理和三角余弦定理得出任意点之间的水平距离、高差和斜距, 根据任意测点之间的三角几何关系得到隧道变形; 3D量测法从任意观测点观测若干已知点的方向和距离, 通过坐标变换计算各测点坐标, 根据各测点坐标得到隧道变形。分析结果表明: 采用RDM法和3D量测法量测隧道拱顶下沉的精度评价公式相同, 而量测隧道水平收敛的精度评价公式不同, RDM法的精度优于3D量测法, 且随着全站仪到量测断面距离的增加, 差值逐渐增大, 当距离为100 m时, 两者精度差值已增大至0.43 mm; 在三车道公路隧道中, 当距离为40~60m时, 2种方法量测隧道水平收敛的精度均为最高, RDM法可达0.61~0.68mm, 3D量测法可达0.78~0.84mm; RDM法和3D量测法量测的隧道拱顶下沉曲线平滑、圆顺, 拟合度都大于0.95, 而在量测隧道净空收敛方面, RDM法的曲线拟合度大于0.9, 3D量测法的曲线拟合度小于0.9, 因此, RDM法量测精度优于3D量测法。
- 隧道工程 /
- 隧道变形 /
- 量测精度 /
- 全站仪 /
- 对边量测法 /
- 三维坐标量测法
Abstract: Based on geodesy principles and error propagation laws, the remote distance measurement (RDM) method and 3Dcoordinate measurement method of based on free stationing of total station were analyzed, the accuracy analysis models of tunnel displacement based on the two measuring methods were established, and the mean square error was used to evaluate the measuring accuracy. The formulas of mean square error on the two methods were deduced. Athree-lane highway tunnel was taken as an example to compare and verify the measuring accuracies of the two methods. In RDM method, through gaining the horizontal distance, the elevation difference and slant distance of two random measurement points were gained by the triangulate height measurement principle and the cosine theorem, and the tunnel displacement was obtained according to the trigonometric and geometric relationship between two random measurement points. In 3D measurement method, the directions and distances of several known points were observed from the random observation point, the coordinates of random measurement points were calculated by using the coordinate conversion, and the tunnel displacement was obtained according to the coordinates of random measurement points. Analysis result shows that the accuracy evaluating formulas of RDM method and 3D measurement method computing tunnel vault settlement are same, however, the formulas computing tunnel horizontal convergence are different, and the accuracy of RDM method is higher than 3D measurement method. When the distance of total station and measured profile increases, the measuring accuracy difference of two methods increases. When the distance is 100 m, the accuracy difference increases to 0.43 mm. In three-lane highway tunnel, when the distance is 40-60 m, the measuring accuracies of tunnel horizontal convergences for the two methods are highest, the accuracy of RDM method can reach 0.61-0.68 mm, and the accuracy of 3D measurement method can reach 0.78-0.84 mm. The curves of tunnel vault settlement measured by using RDM method and 3D measurement method are smooth, and the fitting degrees of the curves are greater than 0.95. However, in the aspect of measuring tunnel horizontal convergence, the curve's fitting degree for RDM method is greater than 0.9, and the degree is less than 0.9 for 3D measurement method. So, the measuring accuracy of RDM method is higher than 3D measurement method.
- tunnel engineering /
- tunnel displacement /
- measurement accuracy /
- total station /
- RDM method /
- 3D measurement method

HTML全文

全挂车辆的制动过程较普通车辆有其特殊性, 因为在具体结构上整个全挂车辆的制动车轴并不在一个刚性车架上, 亦即地面制动力最终作用在2个刚体车架上, 故当主车与挂车的制动分配方案不同时(如主车相对于挂车的制动滞后时间不同), 以及因车辆的振动而导致作用于各制动车轴上的制动力不协调时, 都将加剧全挂车辆制动过程的振动。因此, 研究主、挂车之间的这种振动将对全挂车辆制动过程的改善具有十分重要的意义。

车辆制动时的外力是由地面和空气提供的。在车速较低、空气阻力较小的情况下, 则车辆制动的外力主要来自于地面制动力。车辆在制动过程中的振动主要是由于地面制动力的波动和变化引起的, 因而地面制动力是车辆制动时振动的主要激励因素。

在假定车辆制动系统性能稳定及制动路面较平坦的情况下, 地面制动力主要随制动过程中地面附着系数及作用于车轮上的动反力的变化而变化, 在全挂车辆的整个制动过程中, 这两个方面是交互影响的^[1]。而且由于地面附着系数及动反力的变化也并不是一个平稳的随机过程, 因而受此二者影响全挂车辆的制动振动过程将是一个非平稳随机过程。

1.   全挂车辆制动过程的振动动力学分析

1.1   制动过程振动动力学微分方程的建立

假定全挂车辆在无不平度起伏的沥青路面上进行制动, 对牵引车、挂车及挂车悬架分别取隔离体进行动力学分析。考虑到试验用牵引车为无悬挂车辆, 把其简化成如图 1所示的三自由度1/2整车综合振动模型。设k_tv1、k_tv2、c_tv1、c_tv2分别为牵引车前后轮的刚度和阻尼, 则地面对车轮的动反力及制动时的制动力可分别表示为

图 1 牵引车制动过程的动力学分析

下载: 全尺寸图片幻灯片

z11=ctv1(-˙z11)+ktv1(-z11) (1)Fz12=ctv2(-˙z12)+ktv2(-z12) (2)Fx11=Fz11f (3)Fx12=(Fz12+G2)μ1(t) (4) $\begin{array}{l} F_{z 11} = c_{t v 1} (- \dot{z}_{11}) + k_{t v 1} (- z_{11}) (1) \\ F_{z 12} = c_{t v 2} (- \dot{z}_{12}) + k_{t v 2} (- z_{12}) (2) \\ F_{x 11} = F_{z 11} f (3) \\ F_{x 12} = (F_{z 12} + G_{2}) μ_{1} (t) (4) \end{array}$

式中: f为地面滚动阻力系数; G₂为平稳状况下分布于牵引车后轴上的静载荷; μ₁ (t) 为牵引车后轴车轮处的地面附着系数。

滚动阻力及地面制动力所形成的力矩分别为

11=Fx11R1 (5)Μ12=Fx12R2 (6) $\begin{array}{l} Μ_{11} = F_{x 11} R_{1} (5) \\ Μ_{12} = F_{x 12} R_{2} (6) \end{array}$

式中: R₁、R₂分别为牵引车前后轮半径。

对于挂车, 考虑到其为有悬挂车辆, 把其简化成如图 2所示的五自由度1/2整车综合振动模型。设k_tv3、k_tv4、c_tv3、c_tv4分别为挂车前后轮的刚度和阻尼, R₃、R₄分别为挂车前后轮半径, G₄为平稳状况下分布于挂车后轴上的静载荷, μ₂ (t) 为挂车后轴车轮处的地面附着系数, 同时考虑挂车仅有后轴装有气压式制动器, 则按与牵引车同样的分析方法有

图 2 挂车制动过程的动力学分析

下载: 全尺寸图片幻灯片

z21=ctv3(-˙z21)+ktv3(-z21) (7)Fz22=ctv4(-˙z22)+ktv4(-z22) (8)Fx21=Fz21f (9)Fx22=(Fz22+G4)μ2(t) (10)Fzs1=cs1(˙z21-˙zs1)+ks1(z21-zs1) (11)Fzs2=cs2(˙z22-˙zs2)+ks2(z22-zs2) (12)Fxs1=Fx21-m¨x21 (13)Fxs2=Fx22-m¨x22 (14)Μ21=Fx21R3 (15)Μ22=Fx22R4 (16) $\begin{array}{l} F_{z 21} = c_{t v 3} (- \dot{z}_{21}) + k_{t v 3} (- z_{21}) (7) \\ F_{z 22} = c_{t v 4} (- \dot{z}_{22}) + k_{t v 4} (- z_{22}) (8) \\ F_{x 21} = F_{z 21} f (9) \\ F_{x 22} = (F_{z 22} + G_{4}) μ_{2} (t) (10) \\ F_{z s 1} = c_{s 1} (\dot{z}_{21} - \dot{z}_{s 1}) + k_{s 1} (z_{21} - z_{s 1}) (11) \\ F_{z s 2} = c_{s 2} (\dot{z}_{22} - \dot{z}_{s 2}) + k_{s 2} (z_{22} - z_{s 2}) (12) \\ F_{x s 1} = F_{x 21} - m \ddot{x}_{21} (13) \\ F_{x s 2} = F_{x 22} - m \ddot{x}_{22} (14) \\ Μ_{21} = F_{x 21} R_{3} (15) \\ Μ_{22} = F_{x 22} R_{4} (16) \end{array}$

对于牵引车和挂车, 分别应用Newton-Euler矢量法建立其动力学微分方程如下

1¨z1=Fz11+Fz12 (17)Μ1¨x1=Fc0+Fk0+Fx11+Fx21 (18)Ιφ1¨φ1=Fz11l1-Fx11h1-Fz12l2-Fx12h2- (Fc0+Fk)h0-Μ11-Μ22 (19)Μ2¨z2=Fzs1+Fzs2 (20)Μ2¨x2=Fxs1+Fxs2-Fc0-Fk0 (21)Ιφ2¨φ2=Fzs1l3-Fxs1h3-Fzs2l4-Fxs2h4+ (Fc0+Fk)h3-Μ21-Μ22 (22)m¨z21=Fz21-Fzs1 (23)m¨z22=Fz22-Fzs2 (24) $\begin{array}{l} Μ_{1} \ddot{z}_{1} = F_{z 11} + F_{z 12} (17) \\ Μ_{1} \ddot{x}_{1} = F_{c 0} + F_{k 0} + F_{x 11} + F_{x 21} (18) \\ Ι_{φ 1} \ddot{φ}_{1} = F_{z 11} l_{1} - F_{x 11} h_{1} - F_{z 12} l_{2} - F_{x 12} h_{2} - \\ (F_{c 0} + F_{k}) h_{0} - Μ_{11} - Μ_{22} (19) \\ Μ_{2} \ddot{z}_{2} = F_{z s 1} + F_{z s 2} (20) \\ Μ_{2} \ddot{x}_{2} = F_{x s 1} + F_{x s 2} - F_{c 0} - F_{k 0} (21) \\ Ι_{φ 2} \ddot{φ}_{2} = F_{z s 1} l_{3} - F_{x s 1} h_{3} - F_{z s 2} l_{4} - F_{x s 2} h_{4} + \\ (F_{c 0} + F_{k}) h_{3} - Μ_{21} - Μ_{22} (22) \\ m \ddot{z}_{21} = F_{z 21} - F_{z s 1} (23) \\ m \ddot{z}_{22} = F_{z 22} - F_{z s 2} (24) \end{array}$

将式(1) ~ (16) 代入式(17) ~ (24), 并考虑有关牵引车与挂车的几何尺寸关系及其相应坐标变换关系, 则整理后并写成矩阵形式为

Μ0]{⋅⋅X}+[C]t{˙X}+[Κ]t{X}={Q}t (25) $[Μ_{0}] {\overset{\cdot \cdot}{X}} + [C]_{t} {\dot{X}} + [Κ]_{t} {X} = {Q}_{t} (25)$

1.2   制动时全挂车辆系统振动的激励因素分析与描述

车辆在硬路面上制动时, 其地面附着系数μ与车轮的滑移率有关(如图 3所示), 在制动的开始阶段, 地面附着系数随车轮滑移率的增大而增大, 当轮胎的滑移率达到20%左右时, 地面附着系数达到最大值μ_p, 称其为峰值附着系数。随后随着滑移率的再增加, 地面附着系数有所下降, 滑移率达到100%, 即车轮完全抱死拖滑时的地面附着系数称为滑动附着系数μ_s。这种变化波动规律决定了地面作用于车轮上的制动力的大小及其变化波动规律, 同时也决定了车辆制动减速度的大小及其变化规律。这可以从车辆制动时汽车制动减速度与制动时间的关系曲线中明显地看出来^[2]。

图 3 附着系数与滑移率关系曲线图

下载: 全尺寸图片幻灯片

由此可见, 车辆制动时地面与车轮之间的附着系数确实是影响地面制动力的主要因素, 如式(4)、式(10) 所示。随着制动过程中附着系数μ₁ (t)、μ₂ (t) 的变化, 地面制动力也随之改变, 引起车辆的振动, 并导致制动轮上垂直动反力F_z12、F_z22的变化, 随后地面制动力受路面附着系数与垂直动反力的共同影响而不断波动, 导致车辆更强烈的制动振动。

所以, 在由方程式(25) 所表达的全挂车辆制动振动系统中, 可以把地面附着系数作为振动激励因素。文献[3]根据图 3所示附着系数与滑移率的变化关系, 通过分段回归得到了全挂车辆在沥青路面上制动时附着系数随滑移率的变化曲线, 尽管滑移率也是制动时间的函数, 但在应用上还是不便, 需寻求制动附着系数随制动时间而变化的关系表达式。

对于主车, 假定其单独制动, 考虑式(4) 中地面制动力的线性主部, 即由G₂引起的地面制动力部分F_xb1, 则有

xb1=μ1(t)G2=l1μ1(t)l1+l2Μ1g (26) $F_{x b 1} = μ_{1} (t) G_{2} = \frac{l_{1} μ_{1} (t)}{l_{1} + l_{2}} Μ_{1} g (26)$

则主车的制动减速度为

1=l1l1+l2μ1(t)g (27) $j_{1} = \frac{l_{1}}{l_{1} + l_{2}} μ_{1} (t) g (27)$

图 4 车辆制动减速度简化模型

下载: 全尺寸图片幻灯片

由此可见, 可用车辆的制动减速度近似地表达地面制动附着系数。设沥青路面的滑动附着系数为μ_s, 则制动减速度的简化理论模型可描述为(如图 4所示)

1={00≤t < t1t-t1t2-t1jmt1≤t < t2jmt≥t2 (28) $j_{1} = {\begin{matrix} 0 & 0 \leq t < t_{1} \\ \frac{t - t_{1}}{t_{2} - t_{1}} j_{m} & t_{1} \leq t < t_{2} \\ j_{m} & t \geq t_{2} \end{matrix} (28)$

比较式(27)、式(28), 则主车制动时地面附着系数随时间的变化规律为

对于挂车, 设挂车先于主车制动的时间差为t₀, 则同理据式(29) 挂车制动时地面附着系数的数学模型为

2(t)={00≤t < t1-t0t-t1+t0t2-t1μst1-t0≤t < t2-t0μst≥t2-t0 (30) $μ_{2} (t) = {\begin{matrix} 0 & 0 \leq t < t_{1} - t_{0} \\ \frac{t - t_{1} + t_{0}}{t_{2} - t_{1}} μ_{s} & t_{1} - t_{0} \leq t < t_{2} - t_{0} \\ μ_{s} & t \geq t_{2} - t_{0} \end{matrix} (30)$

2.   全挂车辆制动过程的仿真分析与试验研究

2.1   时变方程的时城Wilson-θ逐步积分法

方程式(25) 所示的矩阵形式的动力学方程除质量阵外其阻尼阵、刚度阵及激励力列阵皆变为变系数阵, 取时间步长Δt, 按分段线性化原理, 在每一时间步长Δt内将方程式(25) 视为线性时不变方程, 为此方程式(25) 改为增量形式

Μ0]{Δ⋅⋅X}+[C]t{Δ˙X}+[Κ]t{ΔX}={ΔQ}t (31) $[Μ_{0}] {Δ \overset{\cdot \cdot}{X}} + [C]_{t} {Δ \dot{X}} + [Κ]_{t} {Δ X} = {Δ Q}_{t} (31)$

对式(31) 应用Wilson-θ逐步积分法, 在时域内进行响应分析, 即可求得全挂车辆在制动过程中对应各广义坐标的位移、速度、加速度等时域响应值, 进而可以对全挂车辆的制动过程进行时域响应分析。

2.2   全挂车辆制动过程的时域响应仿真分析与试验

按照上述方法, 取θ=1.5^[4], 对式(31) 应用Wilson-θ法进行逐步积分, 并采用MATLAB语言编程进行了全挂车辆制动过程的仿真计算, 分析了全挂车辆在沥青路面上制动时牵引力的变化波动状况及其制动稳定性状况。为了验证上述全挂车辆制动振动过程动力学模型及时域仿真分析的正确性, 在沥青路面上进行了全挂车辆的制动试验, 根据试验测定全挂车辆的制动器起作用时间为0.7 s, 主车制动滞后时间为0.5 s, 试验条件、信号测量、实验方法见参考文献[1]。

图 5 制动初速度v=4.12 m/s时牵引架牵引力的变化状况

下载: 全尺寸图片幻灯片

图 6 制动初速度v=6.43 m/s时牵引架牵引力的变化状况

下载: 全尺寸图片幻灯片

图 5、图 6所示为全挂车辆在两种不同制动初速度条件下制动时其牵引架牵引力变化波动状况的时域仿真分析与试验结果对比, 图中牵引力为正时表示牵引架受拉力, 为负时表示牵引架受压力。

分析图 5、图 6所示的仿真与试验结果可以得出如下结论:

(1) 在各种制动初速度水平下制动时, 牵引架牵引力的仿真分析结果与试验结果相吻合, 这说明前述全挂车辆的制动模型及其制动过程动力学分析是正确的和可靠的;

(2) 无论何种初速度下制动, 牵引架牵引力的大致变化趋势都是先增大, 约经过0.5 s的时间后开始减小, 这与全挂车辆各制动车轴的制动顺序相吻合, 因为主车的制动滞后时间约为0.5 s, 当开始制动时, 挂车车轮先受到地面制动力的作用而减速, 而主车由于制动滞后还在按原速度运动;

(3) 随着制动初速度的增加, 牵引架上牵引力的波动幅值范围增大, 如当制动初速度为v=4.12 m/s时, 仿真结果和试验结果分别为16.9359 kN和18.685 kN; 制动初速度为v=6.43 m/s时, 二者分别为26.027 kN和28.1512 kN。由图示结果还可以看出, 随着制动初速度的增加, 牵引架牵引力的负峰值也增大, 由此可见, 全挂车辆的行驶速度越高, 制动时造成的挂车对主车的冲撞力越大, 对全挂车辆的行驶安全性影响也越大。

3.   结语

根据全挂车辆制动过程的特殊性, 建立了全挂车辆制动时的动力学分析模型, 进行了全挂车辆制动过程的仿真分析, 并进行了相应的试验研究, 正确描述了全挂车辆制动时的全车振动状况及牵引架牵引力的变化波动状况, 这为全挂车辆制动过程的进一步改善奠定了基础。

图 1 RDM法量测隧道变形模型

Figure 1. Measurement model of tunnel displacement with RDM method

下载: 全尺寸图片幻灯片

图 2 RDM法量测原理

Figure 2. Measurement principle of RDM method

下载: 全尺寸图片幻灯片

图 3 3D量测法量测隧道变形模型

Figure 3. Measurement model of tunnel displacement with 3D measurement method

下载: 全尺寸图片幻灯片

图 4 3D量测法量测原理

Figure 4. Measurement principle of 3D measurement method

下载: 全尺寸图片幻灯片

图 5 RDM法测点布置

Figure 5. Layout of measuring points in RDM method

下载: 全尺寸图片幻灯片

图 6 3D量测法测点布置

Figure 6. Layout of measuring points in 3D measurement method

下载: 全尺寸图片幻灯片

图 7 精度计算结果对比

Figure 7. Comparison of calculation results for measuring accuracy

下载: 全尺寸图片幻灯片

图 8 拱顶下沉空间曲线对比

Figure 8. Comparison of space curves for vault settlement

下载: 全尺寸图片幻灯片

图 9 水平收敛空间曲线对比

Figure 9. Comparison of space curves for level convergence

下载: 全尺寸图片幻灯片

表 1 RDM法量测中误差

Table 1. Mean square errors with RDM method

下载: 导出CSV

表 2 3D量测法量测中误差

Table 2. Mean square errors with 3Dmeasurement method

下载: 导出CSV

参考文献(24)

[1]	SCHUBERT W, STEINDORFER A, BUTTON A E. Displacement monitoring in tunnels—an overview[J]. Felsbau, 2002, 20 (2): 7-15.
[2]	AYDIN A, OZBEK A, ACAR A. Geomechanical characterization, 3-D optical monitoring and numerical modeling in Kirkgecit-1Tunnel, Turkey[J]. Engineering Geology, 2014, 181: 38-47. doi: 10.1016/j.enggeo.2014.08.010
[3]	KOVARI K, AMSTAD C. Decision making in tunneling based on field measurements[R]. Zürich: Swiss Federal Institute of Technology, 1993.
[4]	陈建勋, 杨忠, 袁雪戡. 秦岭终南山特长公路隧道大埋深段施工监测及分析[J]. 建筑科学与工程学报, 2006, 23 (3): 71-75. doi: 10.3321/j.issn:1673-2049.2006.03.014 CHEN Jian-xun, YANG Zhong, YUAN Xue-kan. Construction monitoring and measuring in segments of large embedded depth in Qinling Zhongnanshan Super-Long Highway Tunnel[J]. Journal of Architecture and Civil Engineering, 2006, 23 (3): 71-75. (in Chinese). doi: 10.3321/j.issn:1673-2049.2006.03.014
[5]	叶飞, 丁文其, 朱合华, 等. 公路隧道现场监控量测及信息反馈[J]. 长安大学学报: 自然科学版, 2007, 27 (5): 79-83. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200705019.htm YE Fei, DING Wen-qi, ZHU He-hua, et al. Site monitoring and information feedback of highway tunnel[J]. Journal of Chang'an University: Natural Science Edition, 2007, 27 (5): 79-83. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200705019.htm
[6]	陈建勋, 王梦恕, 轩俊杰, 等. 两车道公路黄土隧道变形规律[J]. 交通运输过程学报, 2012, 12 (3): 9-18. https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201203005.htm CHEN Jian-xun, WANG Meng-shu, XUAN Jun-jie, et al. Deformation rule of loess highway tunnel with two lanes[J]. Journal of Traffic and Transportation Engineering, 2012, 12 (3): 9-18. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201203005.htm
[7]	赖金星, 樊浩博, 来弘鹏, 等. 软弱黄土隧道变形规律现场测试与分析[J]. 岩土力学, 2015, 36 (7): 2003-2012, 2020. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201507030.htm LAI Jin-xing, FAN Hao-bo, LAI Hong-peng, et al. In-situ monitoring and analysis of tunnel deformation law in weak loess[J]. Rock and Soil Mechanics, 2015, 36 (7): 2003-2012, 2020. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201507030.htm
[8]	DUNNICLIFF J. Geotechnical Instrumentation for Monitoring Field Performance[M]. New York: Wiley-Interscience, 1993.
[9]	SIMEONI L, ZANEI L. A method for estimating the accuracy of tunnel convergence measurements using tape distometers[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46: 796-802. doi: 10.1016/j.ijrmms.2008.11.004
[10]	KAVVADAS M J. Monitoring ground deformation in tunnelling: current practice in transportation tunnels[J]. Engineering Geology, 2005, 79: 93-113. doi: 10.1016/j.enggeo.2004.10.011
[11]	王浩, 葛修润, 宋罡, 等. 全站仪在隧道开挖施工三维变形监测中的应用[J]. 岩石力学与工程学报, 1999, 18 (增): 1217-1219. WANG Hao, GE Xiu-run, SONG Gang, et al. Application of total station in 3-D deformation monitoring during tunnel excavation[J]. 1999, 18 (S): 1217-1219. (in Chinese).
[12]	谭俊玲. 全站仪遥测技术在乌鞘岭铁路隧道围岩变形监测中的应用[J]. 现代隧道技术, 2004, 41 (4): 51-54. doi: 10.3969/j.issn.1009-6582.2004.04.009 Tan Jun-ling. Application of the remote sensing technology with a total-station to monitor the deformations of surrounding rock in Wushaoling Railway Tunnel[J]. Modern Tunnelling Technology, 2004, 41 (4): 51-54. (in Chinese). doi: 10.3969/j.issn.1009-6582.2004.04.009
[13]	田胜利, 葛修润, 涂志军. 隧道及地下空间结构变形的数字化近景摄影测量试验研究[J]. 岩石力学与工程学报, 2006, 25 (7): 1309-1315. doi: 10.3321/j.issn:1000-6915.2006.07.003 TIAN Sheng-li, GE Xiu-run, TU Zhi-jun. Testing study on digital close-range photogrammetry for measuring deformations of tunnel and underground spaces[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25 (7): 1309-1315. (in Chinese). doi: 10.3321/j.issn:1000-6915.2006.07.003
[14]	刘大刚, 王明年. 基于数码摄影技术的隧道围岩变形非接触量测方法研究[J]. 现代隧道技术, 2007, 44 (3): 22-25. doi: 10.3969/j.issn.1009-6582.2007.03.005 LIU Da-gang, WANG Ming-nian. Study on the non-contact measurement of tunnel surrounding rock deformation based on digital photogrammetry[J]. Modern Tunnelling Technology, 2007, 44 (3): 22-25. (in Chinese). doi: 10.3969/j.issn.1009-6582.2007.03.005
[15]	MAHDEVARI S, TORABI S R. Prediction of tunnel convergence using Artificial Neural Networks[J]. Tunnelling and Underground Space Technology, 2012, 28: 218-228. doi: 10.1016/j.tust.2011.11.002
[16]	罗彦斌, 陈建勋. 土质浅埋隧道CRD法施工中隔壁变形监测与分析[J]. 现代隧道技术, 2011, 48 (6): 105-109. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201106021.htm LUO Yan-bin, CHEN Jian-xun. Monitoring and analysis of the deformation of the middle wall during the construction of a shallow soil tunnel by the CRD method[J]. Modern Tunnelling Technology, 2011, 48 (6): 105-109. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201106021.htm
[17]	罗彦斌, 陈建勋. 隧道水平围岩压力计算方法[J]. 交通运输工程学报, 2012, 12 (2): 10-17. http://transport.chd.edu.cn/article/id/201202002 LUO Yan-bin, CHEN Jian-xun. Calculation method of horizontal surrounding rock pressure for tunnel[J]. Journal of Traffic and Transportation Engineering, 2012, 12 (2): 10-17. (in Chinese). http://transport.chd.edu.cn/article/id/201202002
[18]	LUO Yan-bin, CHEN Jian-xun, HUANG Pei, et al. Deformation and mechanical model of temporary support sidewall in tunnel cutting partial section[J]. Tunnelling and Underground Space Technology, 2017, 61: 40-49.
[19]	LUO Yan-bin, CHEN Jian-xun, WANG Hong-yu, et al. Deformation rule and mechanical characteristics of temporary support in soil tunnel constructed by sequential excavation method[J]. KSCE Journal of Civil Engineering, 2016, DOI: 10.1007/s12205-016-0978-3.
[20]	宋冶. 自由设站法三维变形观测精度的检测[J]. 工程勘察, 1999 (1): 61-63. https://www.cnki.com.cn/Article/CJFDTOTAL-GCKC901.017.htm SONG Ye. Inspection on the precision of 3D deformation observation of free stationing method[J]. Geotechnical Investigation and Surveying, 1999 (1): 61-63. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCKC901.017.htm
[21]	杨松林, 刘维宁, 王梦恕, 等. 自动全站仪隧道围岩变形非接触监测及分析预报系统研究[J]. 铁道学报, 2004, 26 (3): 93-97. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200403018.htm YANG Song-lin, LIU Wei-ning, WANG Meng-shu, et al. Study on the auto-total station system for monitoring analyzing and forecasting tunnel country rock deformation[J]. Journal of the China Railway Society, 2004, 26 (3): 93-97. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200403018.htm
[22]	程效军, 缪盾. 全站仪自由设站法精度探讨[J]. 铁道勘察, 2008 (6): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-TLHC200806002.htm CHENG Xiao-jun, MIAO Dun. Discussion on accuracy of liberal station method with total station machine[J]. Railway Investigation and Surveying, 2008 (6): 1-4. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TLHC200806002.htm
[23]	袁恒, 刘成龙, 卢杰, 等. 全站仪三维自由设站隧道非接触监控量测原理及精度分析[J]. 工程勘察, 2012 (8): 63-67. https://www.cnki.com.cn/Article/CJFDTOTAL-GCKC201208015.htm YUAN Heng, LIU Cheng-long, LU Jie, et al. The principle and accuracy analysis of non-contact monitoring for tunnel based on free station of total station[J]. Geotechnical Investigation and Surveying, 2012 (8): 63-67. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCKC201208015.htm
[24]	LUO Yan-bin, CHEN Jian-xun, XI Wei-zheng, et al. Analysis of tunnel displacement accuracy with total station[J]. Measurement, 2016, 83: 29-37.