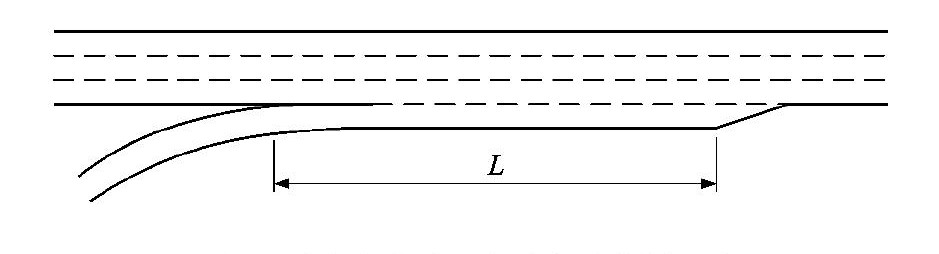
Calculation method of parallel-type acceleration lane length of urban expressway
-
摘要: 比较了现行中美规范平行式加速车道长度计算方法的差异, 结合运动学模型和可接受间隙理论, 在考虑主线交通水平、初始速度与可变间隙3种影响因素的基础上, 建立了城市快速路平行式加速车道长度计算模型, 采用蒙特卡洛方法求解模型, 分析了3种影响因素对加速车道长度的影响, 并提出了一种基于期望初始速度和期望主线交通水平的加速车道长度确定方法。分析结果表明: 3种影响因素对加速车道长度有较大的影响, 在不同设计时速下, 《城市快速路设计规程》 (CJJ129—2009) 规定的长度最小值均小于仿真值, 在设计时速为100km·h-1时, 三级服务水平上下限的加速车道长度分别比规定的最小值大27~36、9~27 m, 在设计时速为80km·h-1时, 分别大10~22、4~24m, 在设计时速为60km·h-1时, 分别大15~24、13~30m;随着初始速度的减小, 加速车道长度呈现增大趋势; 在相同条件下, 第4种临界间隙函数的加速车道长度最大, 而第1种临界间隙函数的加速车道长度最小, 表明临界间隙越大, 需要的加速车道就越长; 不同设计时速下三级服务水平上下限加速车道长度和初始速度的二次函数拟合度为0.865 8~0.999 7, 因此, 整体拟合效果良好。可见, 本文的快速路平行式加速车道长度计算方法合理、可靠。Abstract: The differences of calculation methods of parallel-type acceleration lane length in Chinese and American current standards were compared. Kinematics model and acceptable gap model were combined, and a calculation model of parallel-type acceleration lane length of urban expressway was established on the basis of considering three kinds of influence factors, including mainline traffic level, initial velocity and variable gap. The model was solved by Monte Carlo method. The influence of three kinds of factors on the acceleration lane length was analyzed, and a determining method of acceleration lane length based on expected initial velocity and expected mainline traffic level was proposed. Analysis result shows that 3 factors have great influence on the acceleration lane length, and the minimum values of acceleration lane length in Specification for Design of Urban Expressway (CJJ 129—2009) are smaller than the simulation values at different design speeds. When the design speed is 100 km·h-1, the upper and lower limits ofacceleration lane length under the third class service level are 27-36 mand 9-27 mlarger than the specified values, respectively. When the design speed is 80 km·h-1, the upper and lower limits of acceleration lane length under the third class service level are 10-22 mand 4-24 mlarger than the specified values, respectively. When the design speed is 60 km·h-1, the upper and lower limits of acceleration lane length under the third class service level are 15-24 mand 13-30 mlarger than the specified values, respectively. With the decrease of initial velocity, the acceleration lane length increases. Under the same condition, the acceleration lane length on the fourth critical gap function is maximum, and the value on the first critical gap function is minimum, which indicates that the larger the critical gap is, the longer the acceleration lane length is. The quadratic function fitting degrees of acceleration lane length and initial velocity are 0.865 8-0.999 7 at different design speeds under the third class service level, which indicates that the whole fitting result is good. Obviously, the calculation method of parallel-type acceleration lane length of urban expressway is reasonable and reliable.
-
表 1 三级服务水平下的速度与流量
Table 1. Velocities and flows under third service level

表 2 设计时速为100km·h-1时加速车道长度仿真结果
Table 2. Simulation result of acceleration lane length at design speed of 100km·h-1

表 3 设计时速为80km·h-1时加速车道长度仿真结果
Table 3. Simulation result of acceleration lane length at design speed of 80km·h-1

表 4 设计时速为60km·h-1时加速车道长度仿真结果
Table 4. Simulation result of acceleration lane length at design speed of 60km·h-1

表 5 设计速度为100km·h-1时加速车道长度和初始速度关系
Table 5. Relationships between acceleration lane length and initial velocity at design speed of 100km·h-1

表 6 设计速度为80km·h-1时加速车道长度和初始速度关系
Table 6. Relationships between acceleration lane length and initial velocity at design speed of 80km·h-1

表 7 设计速度为60km·h-1时加速车道长度和初始速度关系
Table 7. Relationships between acceleration lane length and initial velocity at design speed of 60km·h-1

-
[1] AHAMMED M A, HASSAN Y, SAYED T A. Modeling driver behavior and safety on freeway merging areas[J]. Journal of Transportation Engineering, 2008, 134 (9): 370-377. doi: 10.1061/(ASCE)0733-947X(2008)134:9(370) [2] CHU Tien-dung, MIWA T, MORIKAWA T. Modeling speed adjustment behavior of merging vehicles at urban expressway merging sections[J]. Procedia-Social and Behavioral Sciences, 2014, 138: 116-126. doi: 10.1016/j.sbspro.2014.07.187 [3] SARHAN M, HASSAN Y, HALIM A O. Safety performance of freeway sections and relation to length of speed-change lanes[J]. Canadian Journal of Civil Engineering, 2008, 35 (5): 531-541. doi: 10.1139/L07-135 [4] BREWER M A, FITZPATRICK K, STANLEY J. Driver behavior on speed-change lanes at freeway ramp terminals[J]. Transportation Research Record, 2011 (2223): 54-62. [5] KONDYLI A, ELEFTERIADOU L. Driver behavior at freeway-ramp merging areas: focus group findings[J]. Transportation Research Record, 2009 (2124): 157-166. [6] CHOUDHURY C F, BEN-AKIVA M, TOLEDO T, et al. Modeling cooperative lane changing and forced merging behavior[C]∥TRB. Transportation Research Board 86th Annual Meeting, Washington: TRB, 2007: 1-16. [7] YANG Guang-chuan, XU Hao, TIAN Zong, et al. Acceleration characteristics at metered on-ramps[J]. Transportation Research Record, 2015 (2484): 1-9. [8] YANG Guang-chuan, XU Hao, WANG Zhong-ren, et al. Truck acceleration behavior study and acceleration lane length recommendations for metered on-ramps[J]. International Journal of Transportation Science and Technology, 2016, 5 (2): 93-102. doi: 10.1016/j.ijtst.2016.09.006 [9] YANG Guang-chuan, TIAN Zong, XU Hao, et al. Recommendations for acceleration lane length for metered on-ramps[J]. Transportation Research Record, 2016 (2588): 1-11. [10] FITZPATRICK K, ZIMMERMAN K. Potential updates to2004green book's acceleration lengths for entrance terminals[J]. Transportation Research Record, 2007 (2023): 130-139. [11] HASSAN Y, SARHAN M, SALEHI M. Probabilistic model for design of freeway acceleration speed-change lanes[J]. Transportation Research Record, 2012 (2309): 3-11. [12] FATEMA T, HASSAN Y. Probabilistic design of freeway entrance speed-change lanes considering acceleration and gap acceptance behavior[J]. Transportation Research Record, 2013 (2348): 30-37. [13] FATEMA T, ISMAIL K, HASSAN Y. Validation of probabilistic model for design of freeway entrance speed change lanes[J]. Transportation Research Record, 2014 (2460): 97-106. [14] 贾洪飞, 谭云龙, 李强, 等. 考虑驾驶员特征的快速路合流区间隙接受模型构建[J]. 吉林大学学报: 工学版, 2015, 45 (1): 55-61. https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201501009.htmJIA Hong-fei, TAN Yun-long, LI Qiang, et al. Gap acceptance model of expressway weaving area based on driver characteristics[J]. Journal of Jilin University: Engineering and Technology Edition, 2015, 45 (1): 55-61. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201501009.htm [15] 谭云龙. 快速路合流区微观交通仿真车道变换模型研究[D]. 长春: 吉林大学, 2014.TAN Yun-long. Study on lane-changing model for expressway weaving area in microscopic traffic simulation[D]. Changchun: Jilin University, 2014. (in Chinese). [16] 智永锋, 张骏, 史忠科. 高速公路加速车道长度设计与车辆汇入模型研究[J]. 中国公路学报, 2009, 22 (2): 93-97. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200902016.htmZHI Yong-feng, ZHANG Jun, SHI Zhong-ke. Research on design of expressway acceleration lane length and merging model of vehicle[J]. China Journal of Highway and Transport, 2009, 22 (2): 93-97. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200902016.htm [17] 关羽, 张宁, 朱吉双, 等. 考虑驾驶员行为变化的入口匝道通行能力模型[J]. 交通运输系统工程与信息, 2010, 10 (1): 122-127. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201001018.htmGUAN Yu, ZHANG Ning, ZHU Ji-shuang, et al. Modeling on-ramp capacity with driver behavior variation[J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10 (1), 122-127. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201001018.htm [18] 徐秋实, 任福田, 孙小端, 等. 高速公路互通式立交加速车道长度的研究[J]. 北京工业大学学报, 2007, 33 (3): 298-301. doi: 10.3969/j.issn.0254-0037.2007.03.015XU Qiu-shi, REN Fu-tian, SUN Xiao-rui, et al. Research on the length of acceleration lane at freeway interchange[J]. Journal of Beijing University of Technology, 2007, 33 (3): 298-301. (in Chinese). doi: 10.3969/j.issn.0254-0037.2007.03.015 [19] 邵长桥, 杨振海, 陈金川, 等. 一种确定加速车道长度的概率统计模型[J]. 数理统计与管理, 2004, 20 (4): 42-45. https://www.cnki.com.cn/Article/CJFDTOTAL-SLTJ200104007.htmSHAO Chang-qiao, YANG Zhen-hai, CHEN Jin-chuan, et al. A probability model for length of acceleration lanes on expressway[J]. Application of Statistics and Management, 2004, 20 (4): 42-45. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SLTJ200104007.htm [20] 罗京, 谭云龙, 韩印. 快速路合流区加速车道长度设置方法研究[J]. 计算机工程与应用, 2015, 51 (9): 248-251. doi: 10.3778/j.issn.1002-8331.1407-0276LUO Jing, TAN Yun-long, HAN Yin. Length design method of acceleration lane on expressway weaving area[J]. Computer Engineering and Applications, 2015, 51 (9): 248-251. (in Chinese). doi: 10.3778/j.issn.1002-8331.1407-0276 [21] KIM J T, KIM J, CHANG M. Lane-changing gap acceptance model for freeway merging in simulation[J]. Canadian Journal of Civil Engineering, 2008, 35 (3): 301-311. [22] YANG Guang-chuan, XU Hao, TIAN Zong, et al. Vehicle speed and acceleration profile study for metered on-ramps in California[J]. Journal of Transportation Engineering, 2015, 142 (2): 1-13. [23] HWANG S Y, PARK C H. Modeling of the gap acceptance behavior at a merging section of urban freeway[C]∥Eastern Asia Society for Transportation. 6th Conference of the Eastern-Asia-Society for Transportation Studies. Tokyo: Eastern Asia Society for Transportation, 2005: 1641-1656. [24] LEE G. Modeling gap acceptance at freeway merges[D]. Massachusetts: Massachusetts Institute of Technology, 2006. [25] 邵孜科, 李文权, 孙春洋, 等. 基于蒙特卡罗模拟的平行式加速车道长度模型[J]. 公路交通科技, 2017, 34 (1): 137-142, 148. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK201701020.htmSHAO Zi-ke, LI Wen-quan, SUN Chun-yang, et al. A model of parallel type acceleration lane length based on monte carlo simulation[J]. Journal of Highway and Transportation Research and Development, 2017, 34 (1): 137-142, 148. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK201701020.htm -





 下载:
下载: