PBL加劲型矩形钢管混凝土受拉节点热点应力集中系数计算方法

刘永健; 姜磊; 熊治华; 张国靖; AmirFAM

PBL加劲型矩形钢管混凝土受拉节点热点应力集中系数计算方法

刘永健^1,,
姜磊^{1, 2},
熊治华³,
张国靖¹,
AmirFAM²

1.
长安大学公路学院, 陕西西安 710064
2.
安大略女王大学土木工程系, 安大略金斯顿 K7L 3N6
3.
同济大学土木工程学院, 上海 200092

基金项目:

国家自然科学基金项目 51378068

国家重点研发计划项目 2016YFCO701202

中央高校基本科研业务费专项资金项目 310821175015

详细信息

作者简介:
刘永健(1966-), 男, 江西玉山人, 长安大学教授, 工学博士, 从事桥梁工程研究

中图分类号: U441.5
计量
- 文章访问数: 690
- HTML全文浏览量: 106
- PDF下载量: 1037
- 被引次数: 0
出版历程
- 收稿日期: 2017-08-12
- 刊出日期: 2017-10-25

Hot spot SCF computation method of concrete-filled and PBL-stiffened rectangular hollow section joint subjected to axial tensions

1.
School of Highway, Chang'an University, Xi'an 710064, Shaanxi, China
2.
Department of Civil Engineering, Queen's University, Kingston K7L 3N6, Ontario, Canada
3.
College of Civil Engineering, Tongji University, Shanghai 200092, China

More Information

Author Bio:
LIU Yong-jian(1966-), male, professor, PhD, lyj.lyj.chd@gmail.com

摘要

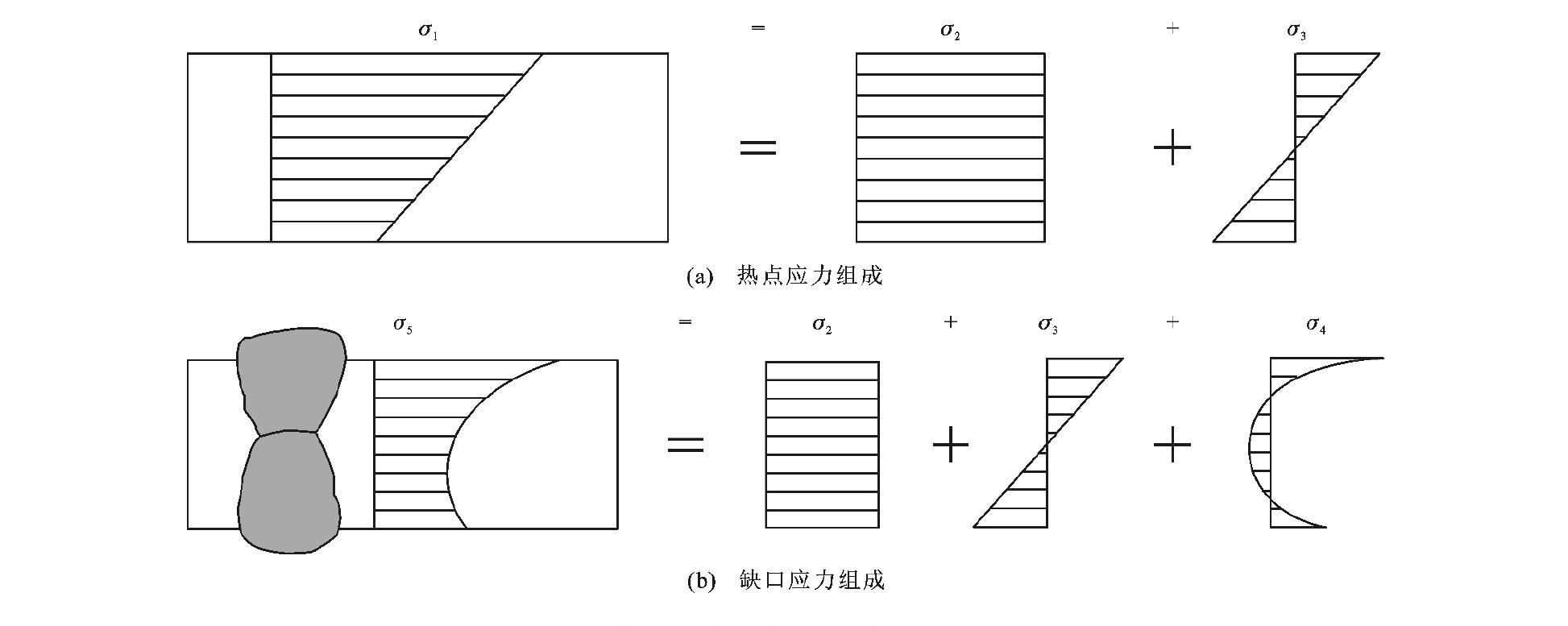
摘要: 考虑了PBL加劲型矩形钢管混凝土支管受拉节点支主管宽度比与厚度比和主管宽厚比, 建立了热点应力集中系数有限元模型, 计算了支主管节点热点应力集中系数; 基于最小二乘法对计算结果进行拟合, 给出不同几何参数下节点热点应力集中系数计算公式, 对比了矩形钢管节点和PBL加劲型矩形钢管混凝土节点应力集中系数和荷载幅。计算结果表明: 采用有限元模型计算的热点应力集中系数曲线与静力试验曲线基本一致, 支主管交汇处各位置热点应力集中系数有限元计算结果与CIDECT规范公式计算结果平均比值分别为1.006、1.007、1.013、1.015和0.987, 两者差值小于15%, 因此, 有限元模型可靠; PBL加劲型矩形钢管混凝土支管受拉节点热点应力集中系数变化规律基本一致, 随支主管宽度比呈抛物线变化, 在0.6⁰.8之间达到最大值, 随主管宽厚比和支主管厚度比增大而增大, 与CIDECT规范中矩形钢管节点计算结果一致; 拟合得到的PBL加劲型矩形钢管混凝土节点热点应力集中系数公式计算结果与有限元计算结果的平均比值为1.011, 均方差为0.222, 变异系数为0.219, 说明了拟合公式准确; 采用应力集中系数计算公式, 将PBL加劲型矩形钢管混凝土节点与矩形钢管节点进行对比, PBL加劲型矩形钢管混凝土节点支管热点应力集中系数下降了68%以上, 主管热点应力集中系数下降了61%以上, 在2.0×106循环次数作用下, 容许荷载幅提高到3倍以上。
- 桥梁工程 /
- PBL加劲型矩形钢管混凝土节点 /
- 热点应力集中系数 /
- 有限元分析 /
- 容许荷载幅
Abstract: The width ratio and thickness ratio of brace to chord and the width-to-thickness ratio of chord for concrete-filled and PBL-stiffened rectangular hollow section joint subjected to axial tensions were considered, and the finite element model of hot spot stress concentration factor (SCF) was established.The computation result of hot spot SCF was fitted by the least square method, the SCF computation formulas under different geometric parameters were proposed, andthe hot spot SCFs and load ranges of rectangular hollow section joint and concrete-filled rectangular hollow section joint stiffened with PBLs were compared by using the proposed formulas.Computation result shows that the SCF curve calculated by using the finite element model is almost consistent with the experiment curve obtained by the static test, and the average ratios of finite element calculation results to CIDECT calculation results are 1.006, 1.007, 1.013, 1.015 and 0.987 at the hot spots at the joint of brace and chord, respectively, and the differences are less than 15%, which verifies the reliability of finite element model.The SCFs of concrete-filled and PBL-stiffened rectangular hollow section joint subjected to axial tensions have the similar variation trend and change in parabola shape with the width ratio of brace to chord.The maximum value of SCF appears when the width of brace to chord is between 0.6 and 0.8, and increases when the width-to-thickness ratio of chord and the thickness ratio of brace to chord increase, which is same with the SCF of rectangular hollow section joint calculated by CIDECT.The computation formulas and finite element model of hot spot SCF of concrete-filled and PBLstiffened rectangular hollow section joint subjected to axial tensions are compared, the SCF average ratio is 1.011, the mean variance is 0.222, and the variation coefficient is 0.219, which proves that the fitting formulas are accurate and reliable.Concrete-filled and PBL-stiffened rectangular hollow section joint is compared with rectangular hollow section joint, the SCFs of brace and chord computed by using the proposed formulas decrease by more than 68% and 61%, respectively, and the allowable load ranges increase to more than three times under the action of 2.0×10⁶ cycle times.
- bridge engineering /
- concrete-filled and PBL-stiffened rectangular hollow section joint /
- hot spot stress concentration factor /
- finite element analysis /
- allowable load range

HTML全文

图 1 热点应力和缺口应力组成

Figure 1. Constitutions of hot spot stress and notch stress

下载: 全尺寸图片幻灯片

图 2 热点应力可能发生位置

Figure 2. Possible appearing locations of hot spot stress

下载: 全尺寸图片幻灯片

图 3 热点应力外推法

Figure 3. Extrapolation methods of hot spot stress

下载: 全尺寸图片幻灯片

图 4 焊缝构造

Figure 4. Weld structures

下载: 全尺寸图片幻灯片

图 5 节点构造

Figure 5. Joint structure

下载: 全尺寸图片幻灯片

图 6 节点有限元模型

Figure 6. Finite element model of joint

下载: 全尺寸图片幻灯片

图 7 试件

Figure 7. Specimens

下载: 全尺寸图片幻灯片

图 8 有限元结果与静力试验结果对比

Figure 8. Comparison between finite element and static test results

下载: 全尺寸图片幻灯片

图 9 线A计算结果对比

Figure 9. Calculated results comparison on line A

下载: 全尺寸图片幻灯片

图 10 线B计算结果对比

Figure 10. Calculated results comparison on line B

下载: 全尺寸图片幻灯片

图 11 线C计算结果对比

Figure 11. Calculated results comparison on line C

下载: 全尺寸图片幻灯片

图 12 线D计算结果对比

Figure 12. Calculated results comparison on line D

下载: 全尺寸图片幻灯片

图 13 线E计算结果对比

Figure 13. Calculated results comparison on line E

下载: 全尺寸图片幻灯片

图 14 线A热点应力集中系数

Figure 14. Hot spot stress concentration factors on line A

下载: 全尺寸图片幻灯片

图 15 线B热点应力集中系数

Figure 15. Hot spot stress concentration factors on line B

下载: 全尺寸图片幻灯片

图 16 线C热点应力集中系数

Figure 16. Hot spot stress concentration factors on line C

下载: 全尺寸图片幻灯片

图 17 线D热点应力集中系数

Figure 17. Hot spot stress concentration factors on line D

下载: 全尺寸图片幻灯片

图 18 线E热点应力集中系数

Figure 18. Hot spot stress concentration factors on line E

下载: 全尺寸图片幻灯片

图 19 线F热点应力集中系数

Figure 19. Hot spot stress concentration factors on line F

下载: 全尺寸图片幻灯片

图 20 线G热点应力集中系数

Figure 20. Hot spot stress concentration factors on line G

下载: 全尺寸图片幻灯片

图 21 有限计算元结果与拟合公式计算结果对比

Figure 21. Calculated results comparison using proposed formulas and finite element models

下载: 全尺寸图片幻灯片

图 22 热点应力集中系数对比

Figure 22. Comparison of hot spot stress concentration factors

下载: 全尺寸图片幻灯片

表 1 设计参数

Table 1. Design parameters

下载: 导出CSV

表 2 试件参数

Table 2. Specimen parameters

下载: 导出CSV

表 3 热点应力集中系数计算结果

Table 3. Calculated results of hot spot stress concentration factors

下载: 导出CSV

表 4 荷载幅计算结果

Table 4. Calculated results of load range

下载: 导出CSV

参考文献(34)

[1]	刘永健, 张宁, 张俊光. PBL加劲型矩形钢管混凝土的力学性能[J]. 建筑科学与工程学报, 2012, 29 (4): 13-17. doi: 10.3969/j.issn.1673-2049.2012.04.003 LIU Yong-jian, ZHANG Ning, ZHANG Jun-guang. Mechanical behavior of concrete-filled square steel tube stiffened with PBL[J]. Journal of Architecture and Civil Engineering, 2012, 29 (4): 13-17. (in Chinese). doi: 10.3969/j.issn.1673-2049.2012.04.003
[2]	刘永健, 李慧, 张宁, 等. PBL加劲型矩形钢管混凝土界面粘结-滑移性能[J]. 建筑科学与工程学报, 2015, 32 (5): 1-7. doi: 10.3969/j.issn.1673-2049.2015.05.001 LIU Yong-jian, LI Hui, ZHANG Ning, et al. Interface bond-slip performance of rectangular concrete-filled steel tube stiffened by PBL[J]. Journal of Architecture and Civil Engineering, 2015, 32 (5): 1-7. (in Chinese). doi: 10.3969/j.issn.1673-2049.2015.05.001
[3]	程高, 刘永健, 田智娟, 等. PBL加劲型矩形钢管混凝土不等宽T型节点受拉性能[J]. 长安大学学报: 自然科学版, 2015, 35 (3): 83-90. doi: 10.3969/j.issn.1671-8879.2015.03.013 CHENG Gao, LIU Yong-jian, TIAN Zhi-juan, et al. Tensile behavior of PBL stiffened concrete-filled rectangular steel tubular unequal T-connections[J]. Journal of Chang'an University: Natural Science Edition, 2015, 35 (3): 83-90. (in Chinese). doi: 10.3969/j.issn.1671-8879.2015.03.013
[4]	高诣民, 刘永健, 姜磊, 等. PBL加劲型矩形钢管混凝土桁架受弯性能试验[J]. 建筑科学与工程学报, 2017, 34 (5): 171-180. doi: 10.3969/j.issn.1673-2049.2017.05.019 GAO Yi-min, LIU Yong-jian, JIANG Lei, et al. Experiment on flexural behaviour of rectangular concrete filled steel tubular truss stiffened with PBL[J]. Journal of Architecture and Civil Engineering, 2017, 34 (5): 171-180. (in Chinese). doi: 10.3969/j.issn.1673-2049.2017.05.019
[5]	张宁, 刘永健, 李慧. PBL加劲型矩形钢管混凝土轴压柱局部屈曲性能分析[J]. 建筑科学与工程学报, 2017, 34 (2): 95-102. doi: 10.3969/j.issn.1673-2049.2017.02.013 ZHANG Ning, LIU Yong-jian, LI Hui. Local buckling performance analysis of rectangular concrete-filled steel tubular axial compression column with PBL stiffeners[J]. Journal of Architecture and Civil Engineering, 2017, 34 (2): 95-102. (in Chinese). doi: 10.3969/j.issn.1673-2049.2017.02.013
[6]	张宁, 刘永健, 李慧, 等. 弹性基底上受非均匀荷载加劲板的局部屈曲特性[J]. 交通运输工程学报, 2017, 17 (1): 36-44. doi: 10.3969/j.issn.1671-1637.2017.01.005 ZHANG Ning, LIU Yong-jian, LI Hui, et al. Local buckling characteristics of stiffened rectangular plate on elastic foundation subjected to non-uniform loads[J]. Journal of Traffic and Transportation Engineering, 2017, 17 (1): 36-44. (in Chinese). doi: 10.3969/j.issn.1671-1637.2017.01.005
[7]	刘永健, 李慧, 张宁. 非均匀受压矩形钢管混凝土局部弹性屈曲分析[J]. 建筑科学与工程学报, 2015, 32 (4): 1-8. doi: 10.3969/j.issn.1673-2049.2015.04.001 LIU Yong-jian, LI Hui, ZHANG Ning. Local elastic buckling analysis of rectangular concrete-filled steel tube under non-uniform compression[J]. Journal of Architecture and Civil Engineering, 2015, 32 (4): 1-8. (in Chinese). doi: 10.3969/j.issn.1673-2049.2015.04.001
[8]	刘永健, 程高, 张宁, 等. 开孔钢板加劲型方钢管混凝土轴压短柱试验研究[J]. 建筑结构学报, 2014, 35 (10): 39-46. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201410005.htm LIU Yong-jian, CHENG Gao, ZHANG Ning, et al. Experimental research on concrete-filled square steel tubular columns stiffened with PBL[J]. Journal of Building Structures, 2014, 35 (10): 39-46. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201410005.htm
[9]	姜磊, 刘永健, 张俊光. 开孔钢板加劲型方钢管混凝土长柱轴压性能试验研究[J]. 建筑结构学报, 2016, 37 (5): 122-128. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201605013.htm JIANG Lei, LIU Yong-jian, ZHANG Jun-guang. Experimental study on axial compression behavior of concrete-filled square steel tubular long columns stiffened with PBL[J]. Journal of Building Structures, 2016, 37 (5): 122-128. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201605013.htm
[10]	LIU Yong-jian, XIONG Zhi-hua, LUO Ya-lin, et al. Doublecomposite rectangular truss bridge and its joint analysis[J]. Journal of Traffic and Transportation Engineering: English Edition, 2015, 2 (4): 249-257. doi: 10.1016/j.jtte.2015.05.005
[11]	刘彬, 刘永健, 周绪红, 等. 中等跨径装配式矩形钢管混凝土组合桁梁桥设计[J]. 交通运输工程学报, 2017, 17 (4): 20-31. doi: 10.3969/j.issn.1671-1637.2017.04.003 LIU Bin, LIU Yong-jian, ZHOU Xu-hong, et al. Design of mid-span fabricated RCFST composite truss bridge[J]. Journal of Traffic and Transportation Engineering, 2017, 17 (4): 20-31. (in Chinese). doi: 10.3969/j.issn.1671-1637.2017.04.003
[12]	刁砚. 钢管混凝土桥管节点疲劳性能试验研究[D]. 成都: 西南交通大学, 2007. DIAO Yan. Experimental research on fatigue performance of tubular joints in concrete-filled steel bridge[D]. Chengdu: Southwest Jiaotong University, 2007. (in Chinese).
[13]	WANG Qu, NAKAMURA S, CHEN Bao-chun, et al. Fatigue damage of a half-througth concrete-filled steel tubular trussed arch bridge in China[C]∥ASME. The 2015 World Congress on Advances in Structural Engineering and Mechanics. New York: ASME, 2015: 1-12.
[14]	刘永健, 姜磊, 王康宁. 焊接管节点疲劳研究综述[J]. 建筑科学与工程学报, 2017, 34 (5): 1-20. doi: 10.3969/j.issn.1673-2049.2017.05.002 LIU Yong-jian, JIANG Lei, WANG Kang-ning. Review of fatigue behavior in welded tubular joints[J]. Journal of Architecture and Civil Engineering, 2017, 34 (5): 1-20. (in Chinese). doi: 10.3969/j.issn.1673-2049.2017.05.002
[15]	VAN WINGERDE A M. The fatigue behaviour of T and X joints made of square hollow sections[J]. HERON, 1992, 37 (2): 1-182.
[16]	VAN WINGERDE A M, PACKER J A, WARDENIER J. SCF formulae for fatigue design of K-connections between square hollow sections[J]. Journal of Constructional Steel Research, 1997, 43 (1-3): 87-118. doi: 10.1016/S0143-974X(97)00026-6
[17]	TONG L W, ZHENG H Z, MASHITI F R, et al. Stressconcentration factors in circular hollow section and square hollow section T-connections: experiments, finite-element analysis, and formulas[J]. Journal of Structural Engineering, 2013, 139 (11): 1866-1881. doi: 10.1061/(ASCE)ST.1943-541X.0000759
[18]	SCHUMACHER A, NUSSBAUMER A. Experimental study on the fatigue behaviour of welded tubular K-joint for bridges[J]. Engineering Structures, 2006, 28 (5): 745-755. doi: 10.1016/j.engstruct.2005.10.003
[19]	MASHIRI F R, ZHAO Xiao-ling, GRUNDY P. Fatigue tests and design of welded T connections in thin cold-formed square hollow sections under in-plane bending[J]. Journal of Structural Engineering, 2002, 128 (11): 1413-1422. doi: 10.1061/(ASCE)0733-9445(2002)128:11(1413)
[20]	FENG Ran, YOUNG Ben. Design of cold-formed stainless steel tubular T-and X-joints[J]. Journal of Constructional Steel Research, 2011, 67 (3): 421-436. doi: 10.1016/j.jcsr.2010.09.011
[21]	FENG Ran, YOUNG Ben. Stress concentration factors of cold-formed stainless steel tubular X-joints[J]. Journal of Constructional Steel Research, 2013, 91: 26-41. doi: 10.1016/j.jcsr.2013.08.012
[22]	CHIEW S P, LEE C K, LIE S T, et al. Fatigue behaviors of square-to-square hollow section T-joint with corner crack. Ⅰ: experimental studies[J]. Engineering Fracture Mechanics, 2007, 74 (5): 703-720. doi: 10.1016/j.engfracmech.2006.06.022
[23]	UDOMWORARAT P, MIKI C, ICHIKAWAA, et al. Fatigue and ultimate strengths of concrete filled tubular K-joints on truss girder[J]. Journal of Structural Engineering, 2000, 46A: 1627-1635.
[24]	UDOMWORARAT P, MIKI C, ICHIKAWA A, et al. Fatigue performance of composite tubular K-joints for truss type bridge[J]. Structural Engineering/Earthquake Engineering, 2002, 19 (2): 9-23.
[25]	QIAN Xu-dong, JITPAIROD K, MARSHALL P, et al. Fatigue and residual strength of concrete-filled tubular X-joints with full capacity welds[J]. Journal of Constructional Steel Research, 2014, 100: 21-35. doi: 10.1016/j.jcsr.2014.04.021
[26]	WANG Ke, TONG Le-wei, ZHU Jun, et al. Fatigue behavior of welded T-joings with a CHS brace and CFCHS chord under axial loading in the brace[J]. Journal of Bridge Engineering, 2013, 18 (2): 142-152. doi: 10.1061/(ASCE)BE.1943-5592.0000331
[27]	童乐为, 王柯, 史炜洲, 等. 圆管混凝土T型焊接节点热点应力试验研究[J]. 同济大学学报: 自然科学版, 2010, 38 (3): 329-334. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201003005.htm TONG Le-wei, WANG Ke, SHI Wei-zhou, et al. Experimental study on hot spot stress of welded concrete filled CHS T-joints[J]. Journal of Tongji University: Natural Science, 2010, 38 (3): 329-334. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201003005.htm
[28]	XU Fei, CHEN Ju, JIN Wei-liang. Experimental investigation of SCF distribution for thin-walled concrete-filled CHS joints under axial tension loading[J]. Thin-Walled Structrues, 2015, 93 (2): 149-157.
[29]	MASHIRI F R, ZHAO Xiao-ling. Square hollow section (SHS) T-joints with concrete-filled chords subjected to in-plane fatigue loading in the brace[J]. Thin-Walled Structures, 2010, 48 (2): 150-158. doi: 10.1016/j.tws.2009.07.010
[30]	程高, 刘永健, 邱洁霖, 等. PBL加劲型矩形钢管混凝土不等宽T型节点应力集中系数分析[J]. 建筑科学与工程学报, 2014, 31 (4): 74-79. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG201404013.htm CHENG Gao, LIU Yong-jian, QIU Jie-lin, et al. Analysis of stress concentration factor on concrete-filled rectangular steel tube T-joints stiffened with PBL[J]. Journal of Architecture and Civil Engineering, 2014, 31 (4): 74-79. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG201404013.htm
[31]	俞文龙. 矩形钢管混凝土T型受拉节点力学性能分析[D]. 西安: 长安大学, 2015. YU Wen-long. Behavior analysis of rectangular concrete-filled steel tubular T-joint under tension load[D]. Xi'an: Chang'an University, 2015. (in Chinese).
[32]	LIU Yong-jian, XIONG Zhi-hua, FENG Yun-cheng, et al. Concrete-filled rectangular hollow section X joint with perfobond leister rib structural performance study: ultimate and fatigue experimental investigation[J]. Steel and Composite Structures, 2017, 24 (4): 455-465.
[33]	LEE Jae-myung, SEO Jung-kwan, KIM Myung-hyun, et al. Comparison of hot spot stress evaluation methods for welded structures[J]. International Journal of Naval Architecture and Ocean Engineering, 2010, 2 (4): 200-210.
[34]	CHOO Y S, QIAN X D, LIEW J Y R, et al. Static strength of thick-walled CHS X-joints—Part I. New approach in strength definition[J]. Journal of Constructional Steel Research, 2003, 59 (10): 1201-1228. doi: 10.1016/S0143-974X(03)00054-3