0.   引言

目前, 集装箱班轮运输企业主要采用的是以包箱费率(Box Rate) 为主的均一定价方式(Freight of All Kinds, FAK), 即对于绝大多数普通货物, 只是区分集装箱尺寸及相应航线, 按照统一标准计收运费。同时, 实践中有时也会将基本运费和附加费合并在一起, 以包干费(All in Freight) 的形式计收, 此时的运价则称为包干费率, 又称“全包价” (All in Rate)。然而, 从企业经营与管理的角度分析, 这样一种运费计收方式, 除了操作方便之外, 几乎没有任何可取之处。

根据第1系列货运集装箱的标准参数, 业务中最为常用的40 ft与20 ft标准普通杂货集装箱的额定最大总质量分别为30 480 t与24 000 t。而且在近几年的业务中, 有越来越多的重型20 ft箱投入使用, 此类20 ft箱的最大总质量也达到了30 480 t, 与一个标准的40 ft箱相同。此外, 还有少数特种箱的额定值更大, 如20 ft的罐式集装箱的最大总质量可达36 000 t。以目前较为主流的8 000 TEU (Twenty-foot Equivalent Unit, 标准箱) 级的全集箱船为例, 此类船舶的净载重吨约为80 000 t, 即每1 TEU能够平摊到的载重吨(以下简称TEU平摊载重吨) 仅有10 t左右。在很多情况下, 即使其装载的所有集装箱均不超过各自的额定最大质量, 载运船舶也极有可能出现“满载不满舱” (即箱位有余而载质量能力不足) 的情况, 从而造成运力的浪费。正如前文所述, 因为目前集装箱班轮运输企业通常以整箱为单位, 按照均一费率计收运费, 所以箱位浪费的直接后果就是集装箱班轮运输企业收益的损失。面对此问题, 推行与集装箱质量挂钩的等级收费体系是比较好的解决办法, 而从集装箱运输定价的主要特点来看, 采取以二部定价为指导思想的非线性定价方法则最为合理与可行。

唐小我等通过存在两类消费者情况下的二部定价模型推导出了最优二部定价公式, 表明最优边际价格由各类消费者的偏好差异程度及边际生产成本决定, 而固定费用主要取决于对商品具有较低效用评价的消费者的需求, 并推导了固定费用与需求弹性的关系以及最优边际价格的范围^[1]。李克克等对存在两类消费者情况下的最优非线性定价模型进行了多维推广, 展示了一个了解消费者需求分布的厂商如何根据消费者的“自我选择机制”制定出一个可供选择的消费组合菜单^[2], 结果表明, 厂商大大减少了低需求类型消费者的消费数量, 尽可能剥夺更多数量消费者的效用以获取更多的利润。

在航空运输领域, Bodily等研究了在需求不确定的情况下, 何时可减少低等舱位的出售, 并且计算了期望收益值^[3]。Li研究了需求确定情况下的定价问题, 在考虑不同售票等级间购票限制的情况下, 提出了制订最优价格策略的线性规划方法^[4]。Li对文献[4]的研究成果又进行了深入探讨, 在放宽其中的2个假设条件的情况下, 通过论证, 提出了通用的最优价格准则, 并且得出“即使所有等级的机票同时出售, 也可以得到最优价格”的结论^[5]。

可见, 多等级定价问题目前在航空运输领域相对已有研究。但是, 针对集装箱班轮运输的研究仍相对鲜见, 且主要集中在上海海事大学相关学者及研究生的部分著述及论文。许波桅在其硕士论文中对集装箱舱位预售及差别定价问题进行了分析, 并提出了以舱位预售为平台, 开展差别定价的设想^[6]。段朝辉在其硕士论文中对超重箱附加费进行了研究, 该文从增大船公司收益及交叉补贴问题角度出发, 基于对数需求函数建立了超重箱最优定价模型, 但该文也只是得到了一个具有初步启发意义的线性差别定价的基本结论^[7]。

综上, 基于单箱总质量差别的集装箱班轮二部非线性定价问题目前在国内外尚未引起学者们的足够重视, 相关研究也处于刚刚起步的阶段^[8-9], 本文主要就基于单箱总质量的集装箱班轮二部定价问题展开研究。

1.   二部定价的经典模型

在经典论著中, 价格制定者通常被假设面对的是异质消费者, 如果前者获悉后者的偏好, 通常他就可以为后者提供个性化的消费组合, 最常见的如价格/数量、价格/品质等, 从而实现价格歧视。而在本文所研究的问题中, 该组合可体现为价格/质量。

二部定价就是一种较为常见的个性化定价手段, 其经典的基本模型可以表示为

${\rm T}(q)=A+fq(1)$

式(1) 提供了一个位于直线上的定价模型, 其中A为二部价格中的基本价格; f为针对超出基准部分的商品价格; q为超出基准部分的商品数量。与代表纯线性定价的直线不同, 这条直线不一定经过原点。二部定价在实践中应用普遍, 表 1给出了一些常见的例子。

表  1  二部定价的常见应用

Table  1.  Common application of two-part pricing

下载: 导出CSV 

| 显示表格

在集装箱班轮运输行业中, 对于不超过特定基准质量的集装箱, 运输企业可以收取一定的基准运费, 而如果集装箱单箱总质量超过该基准质量, 则应额外收取相应的“偏重箱附加费”, 这一思想正契合了二部定价的核心原理。

由于单一的线性定价通常都不一定是最优的, 因而需要进一步考虑更为一般的非线性二部定价方案。

2.   基于单箱总质量差别定价模型的构建与分析

经济学领域已有相关文献研究了二部定价的基本理论^[2], 对非线性定价原理也进行了一定的论述与证明^[3], 因此, 本文对经济学基本原理不再赘述。

基于二部定价的基本原理, 集装箱班轮运输企业在公布各等级运价时可以采用“基本运费+偏重箱附加费”的形式, 即

${\rm P}{}_i=p+p{}_i(2)$

式中: i为将集装箱按单箱总质量分成的若干等级的序号; P_i为某质量等级的单个集装箱的总运价; p为基本运费率; p_i为相应等级的“偏重箱附加费率”。需要特别说明的是, 不同等级下的“偏重箱附加费率”与集装箱质量之间不一定为线性相关关系。

相应地, 最基本的优化模型即可表达为

$\begin{array}{l}{\rm Z}{}_1=\max {\displaystyle \sum _{i=1}^{n}Q}{}_i{\rm P}{}_i(3)\\ {\displaystyle \sum _{i=1}^{n}Q}{}_i\le Q{}_{\text{t}}(4)\\ {\displaystyle \sum W}\le {\rm N}{}_{\text{D}\text{W}}(5)\\ Q{}_i,{\rm P}{}_i>0(6)\end{array}$

式中: n为将集装箱按照质量进行划分的等级数; Q_i为分属每个质量等级的集装箱数量; Q_t为全船箱位总数; W为每个被载运的集装箱的单箱总质量; N_DW为船舶的净载重吨。当然, 每个集装箱的质量也不能超过其额定极限, 这是集装箱的技术规范, 视为默示条件, 不在模型中体现。

至此, 该问题的求解即可归纳为: 确定各等级区间的上下限; 确定各质量等级区间相应的运价。这2个问题相辅相承, 不可割立。

在实际业务中, 针对具体船舶而言, 上述模型中的Q_t、N_DW是已知的; 而针对具体航线而言, 在一定的市场条件下, 其货源构成与特征也是相对稳定的, 即虽然每个承运集装箱的质量是随机的, 但其概率分布规律可以视为是相对稳定的。根据经济学原理可知, 向集装箱班轮企业托运集装箱的数量变化ΔQ与其运价变化ΔP之间存在一定的映射关系, 不妨设其为V: ΔP→ΔQ。实际业务中, 在其他影响因素不变的情况下, 不同质量等级的集装箱, 其对应的价格与托运数量映射关系通常也是不相同的。

因此, 不同质量等级下价格变化与托运量变化的具体映射关系可表达为

$\{\begin{array}{cc}V{}_1:\text{Δ}{\rm P}{}_1\to \text{Δ}Q{}_1\hfill & 0<W\le w{}_1\hfill \\ V{}_i:\text{Δ}{\rm P}{}_i\to \text{Δ}Q{}_i\hfill & w{}_{i-1}<W\le w{}_i\hfill \\ V{}_n:\text{Δ}{\rm P}{}_n\to \text{Δ}Q{}_n\hfill & w{}_{n-1}<W\le w{}_n=w{}_{\max }\hfill \end{array}(7)$

式中: w_i为各个质量等级区间上限, 特别地, w₁为免收“偏重箱附加费”的基准质量, 而w_max则是单个集装箱总质量的额定极限。不同质量分级下的映射关系V_i, 可根据企业长期积累的统计数据获得。

考虑到大多数集装箱班轮运输企业目前在运价制定时往往忽视集装箱的单箱总质量, 仅简单采用均一定价。因此, 为方便企业的实际应用, 即实现传统均一定价向二部定价的转型, 其变化过程可以通过优化模型进一步具体表达为

$\begin{array}{l}{\rm Z}{}_2=\max {\displaystyle \sum _{i=1}^{n}Q}{}_{\text{c}i}({\rm P}+\text{Δ}{\rm P}{}_i)(8)\\ {\rm P}+\text{Δ}{\rm P}{}_i>0(9)\\ Q{}_{\text{b}i}=Q{}_{\text{b}\text{b}i}+V{}_i(10)\\ Q{}_{\text{c}i}\le Q{}_{\text{b}i}(11)\\ Q{}_{\text{b}i}\le Q{}_{\text{p}i}(12)\\ {\displaystyle \sum _{i=1}^n\stackrel{—}{{\displaystyle W}}}{}_{i}Q{}_{\text{c}i}\le {\rm N}{}_{\text{D}\text{W}}(13)\\ {\displaystyle \sum _{i=1}^{n}Q}{}_{\text{c}i}\le Q{}_{\text{t}}(14)\\ Q{}_{\text{c}i},{\rm P},Q{}_{\text{b}i},Q{}_{\text{b}\text{b}i},Q{}_{\text{p}i},Q{}_{\text{t}}\ge 0(15)\end{array}$

式中: P为原先传统的均一定价价格; ΔP_i为定价方法变化后, 第i级集装箱运价的变化; V_i为ΔP_i与ΔQ_i之间的映射关系; Q_bbi为原先传统均一定价下, 第i级集装箱的托运数; Q_bi定价方法变化后, 第i级集装箱的托运数; Q_ci为定价方法变化后, 第i级集装箱的实际承运数; Q_pi为该港口第i级待运集装箱的总数; $\stackrel{—}{{\displaystyle W}}{}_i$为第i级集装箱的平均质量。

约束条件中, 式(9) 表示变动后的运价大于0;式(10) 表示定价方法改变后, 现在各等级的托运量为原该等级托运量加上相应的变化量; 式(11) 表示各等级集装箱的实际承运量不超过该等级的托运量; 式(12) 表示各等级集装箱的托运量不超过该港口该等级待运集装箱的总量; 式(13) 表示所有承运集装箱的总质量不超过船舶的净载重吨, 为简化模型, 该约束为近似表达, $\stackrel{—}{{\displaystyle W}}{}_i$取相应区间上下限的均值; 式(14) 表示所有承运集装箱的总数量不超过船舶的总箱位数; 式(15) 表示模型中的所有变量, 除ΔP_i符号不定外, 其余变量均为非负。

本模型以传统的均一定价为基础, 完整体现了均一定价向实施基于单箱总质量的二部定价的变化过程, 贴近实际, 且易于操作。待求得各等级的ΔP_i后, 可较为方便地以二部定价的形式, 即P_i=p+p_i的形式对外公布。

3.   模型的求解步骤

本文第2小节构建的模型是一个涉及不确定因素的随机非线性优化模型, 理论上无法直接求得其解析解。但是, 依托具体数据, 通过数学试验则可以获得一系列具有指导意义的结果, 其基本步骤可如下。

(1) 对集装箱质量分布进行基础性的统计学分析, 根据分析结果, 初步确定较为合理的等级区间。

(2) 通过数据分析, 确定V_i: ΔP_i→ΔQ_i, 即各区间ΔP_i与ΔQ_i之间的映射关系。

(3) 求解式(8) ~ (15) 所构成的非线性优化模型。

4.   算例

随机选取某企业在某港口的某个具有代表性航次接受托运的集装箱质量数据进行分析, 具体如下。

4.1   样本数据基本分析与折扣区间确定

将样本集装箱的质量折算为标准箱质量导入SPSS进行统计特征的基础性分析。所得直方图及主要参数的描述性结果见图 1及表 2。样本集装箱折合标准箱数为7 684 TEU, 均值为14.551 4 t, 方差为6.406 22 t。

图  1  样本集装箱总质量分布

Figure  1.  Distribution of sample containers' gross masses

下载: 全尺寸图片 幻灯片

表  2  计算结果1

Table  2.  Computing result 1

样本容量/TEU	有效数值	7 684
	缺失	0
均值/t		14.551 4
标准差/t		6.406 22
最小值/t		1.55
最大值/t		35.68
总和/t		559 063.80

下载: 导出CSV 

| 显示表格

该企业选用了一艘载箱量约为8 000 TEU、净载重吨约为80 000 t的全集装箱船执行该航次。从所抽取样本的单箱总质量均值来看, 其已明显超过船舶的TEU平摊载重吨。由此可见, 所选样本中的“偏重箱”过多, 必然导致船舶在载运过程中“满载不满舱”。若近似采取按照质量从大至小的原则从样本集装箱中选择拒载, 则为了满足船舶的载重吨限制, 最终承运的集装箱最多仅能为6 385 TEU, 这些集装箱的总质量为79 994.42 t。在该情况下, 船舶的箱位利用率仅为79.81%, 而且若采用均一定价, 按800 USD·TEU^-1计收运费, 该航次给运输企业带来的收入为5 108 000 USD。

同时, 也可通过所选样本对该航线的总体托运数据进行参数估计。借助SPSS的输出结果表 3可以发现, 样本均值为14.551 4 t, 95%置信区间的一个观察区间为(14.487 3, 14.615 4), 样本标准差为6.406 22 t, 即可认为总体均值的估计值为14.551 4 t, 总体样本标准差估计值为6.406 22 t。考虑到当前各企业均采取同样的均一定价机制, 上述参数对该港口箱源整体特征的把握也具有相当的参考意义。

表  3  计算结果2

Table  3.  Computing result 2

下载: 导出CSV 

| 显示表格

下面对总体的概率分布进行进一步分析。图 1中的曲线为根据直方图拟合的正态曲线, 从形态上判断, 该分布非常接近正态分布, 但经SPSS对相关数据进单样本Kolmogorov-Smirnov检验后发现, 其并不符合正态分布, 具体检验结果见表 4。

表  4  检验结果

Table  4.  Test results

样本容量/TEU		7 684
正态参数	均值/t	14.551 4
	标准差/t	6.406 22
极差	绝对	0.026
	正	0.026
	负	-0.021
K-S检验的Z值		5.140
双尾显著性		0.000

下载: 导出CSV 

| 显示表格

经MATLAB编程对样本数据进行进一步分析, 并进行非参数检验, 该总体X近似服从左截尾点为1.55, 右截尾点为35.68, 均值为14.55, 方差为41.04的截尾正态分布。

通过推导, 得到左右截尾点分别为a、b的截尾正态分布的密度函数表达式为

X~f (x; $\mu ,\sigma {}^2,a,b)=\{\begin{array}{cc}c{}^{-1}\text{e}{}^{-\frac{(x-\mu ){}^2}{2\sigma {}^2}}& a<x<b\\ 0& \text{其}\text{他}\end{array}(16)$

$c={\displaystyle {\int }_a^b\text{e}}{}^{-\frac{(x-\mu ){}^2}{2\sigma {}^2}}\text{d}xa<b$

基于式(16), 对X的均值与方差表达式进一步进行推导, 显然, 当a为-∞, b为+∞时, c为1, 式(16) 即为正态分布的标准表达式。

$\begin{array}{l}E(X)={\displaystyle {\int }_a^{b}x}f(x;\mu ,\sigma {}^2,a,b)\text{d}x=\\ \mu -c{}^{-1}\sigma {}^2\left[\text{e}{}^{-\frac{(b-\mu ){}^2}{2\sigma {}^2}}-\text{e}{}^{-\frac{(a-\mu ){}^2}{2\sigma {}^2}}\right](17)\end{array}$

D (X) =E (X²) -[E (X) ]²=σ²-c^-1σ²$\begin{array}{l}(b-\mu )\text{e}{}^{-\frac{(b-\mu ){}^2}{2\sigma {}^2}}-\\ (a-\mu )\text{e}{}^{-\frac{(a-\mu ){}^2}{2\sigma {}^2}}\end{array}$

$-c{}^{-2}\sigma {}^4\left[\text{e}{}^{-\frac{(b-\mu ){}^2}{2\sigma {}^2}}-\text{e}{}^{-\frac{(a-\mu ){}^2}{2\sigma {}^2}}\right]{}^2(18)$

由式(17) 可知, 当b-μ=μ-a或a为-∞, b为+∞时, E (X) =μ。

式(17)、(18) 给出了正态分布的数学期望μ、方差σ²与截尾正态分布均值E (X)、方差D (X) 之间的关系。由样本数据得到E (X)、D (X) 的估计值后, 可利用MATLAB软件由式(17)、(18) 解出μ、σ²的估计值。

为通过提高船舶箱位利用率来提高整体收益, 集装箱班轮运输企业需将集装箱质量均值尽量控制在船舶的TEU平摊载重吨水平上, 而从船舶积载的角度来看, 船舶承运的所有集装箱的质量差值也最好能够控制在一个相对较低的水平上。从以上两点可知, 理想的μ、σ值应比当前的实测数据更小为宜。

由经济学原理可知, 如果集装箱运输企业适当降低总质量低于基准质量的集装箱的运价, 并适当提高总质量高于基准质量的集装箱的运价, 则可增加前者的托运量, 并同时降低后者(即“偏重箱”) 的托运量。若托运箱源的质量结构产生上述变化, 该情况下新的均值、方差均会向着更有利用于船舶运力利用的方向变化。

如本文前述, 从船公司合理配载的实际需要来看, 理想的满载情况下, 其所承运的每个集装箱的单箱总质量最好能相对集中地分布于船舶TEU平摊载重吨附近。因此, 文献[7]提出的将增收运费的基准质量定为13 t, 并对差异收费及其等级区间进行线性均匀划分的建议, 并未充分考虑船舶的TEU平摊载重吨及箱源质量的客观分布, 显然不尽合理。基于“激励相容”的基本原理, 船公司对更便于其积载, 且更有利于提高其收益水平的单箱总质量区间可相应扩大, 而对其运力利用有较大负面影响的“偏重箱”, 则应采取更为密集的区间细分, 如有必要, 还需配套采取累进费率。

对上文选取的样本集装箱单箱总质量进行频度分析, 结果见表 5。

表  5  频度分析结果

Table  5.  Frequency analysis results

区间	质量区间/t	样本数/TEU		区间	质量区间/t	样本数/TEU		区间	质量区间/t	样本数/TEU
1	(0, 5]	474		10	(13, 14]	441		19	(22, 23]	223
2	(5, 6]	259		11	(14, 15]	457		20	(23, 24]	161
3	(6, 7]	267		12	(15, 16]	429		21	(24, 25]	152
4	(7, 8]	313		13	(16, 17]	424		22	(25, 26]	130
5	(8, 9]	308		14	(17, 18]	427		23	(26, 27]	93
6	(9, 10]	381		15	(18, 19]	350		24	(27, 28]	74
7	(10, 11]	421		16	(19, 20]	324		25	(28, 29]	50
8	(11, 12]	389		17	(20, 21]	305		26	(29, 30]	31
9	(12, 13]	450		18	(21, 22]	268		27	(30, 36]	83

下载: 导出CSV 

| 显示表格

为使问题简化, 本文采用表 5所示的质量区间作为质量差别定价下的差别定价区间。

4.2   ΔP_i与ΔQ_i的映射关系确定

在真正实现模型应用时, 需要通过大量的数据分析来确定ΔP_i与ΔQ_i的映射关系, 本节假设该映射关系V_i为最简单的线性映射, 即

$\text{Δ}Q{}_i=V{}_i(\text{Δ}{\rm P}{}_i)=k{}_i\text{Δ}{\rm P}k{}_i<0$

式中: k_i为线性函数的系数。

4.3   模型求解

式(8) ~ (15) 所构成的非线性优化模型的求解可通过MATLAB编程实现。为提高运行效率, 可先将优化模型进行矩阵化表示。通过变化k_i的取值规律, 结合本文样本对以下各不同情况下的企业收益变化情况进行分析。

(1) 假设变量k_i恒定, 取其为-0.25, 求解结果见表 6。此假设下的航次总收入为6 419 176 USD, 高于原先的5 108 000 USD。

表  6  试验1的优化结果

Table  6.  Optimizing results of test 1

i	质量区间/t	原托运量/TEU	每标准箱价格变动/USD	每标准箱变动后价格/USD	实际载运量/TEU	变动后托运量/TEU	变动后收入/USD
1	(0, 5]	474	698	1 498	300	300	449 400
2	(5, 6]	259	268	1 068	192	192	205 056
3	(6, 7]	267	284	1 084	196	196	212 464
4	(7, 8]	313	376	1 176	219	219	257 544
5	(8, 9]	308	366	1 166	217	217	253 022
6	(9, 10]	381	512	1 312	253	253	331 936
7	(10, 11]	421	592	1 392	273	273	380 016
8	(11, 12]	389	528	1 328	257	257	341 296
9	(12, 13]	450	650	1 450	288	288	417 600
10	(13, 14]	441	632	1 432	283	283	405 256
11	(14, 15]	457	664	1 464	291	291	426 024
12	(15, 16]	429	608	1 408	277	277	390 016
13	(16, 17]	424	598	1 398	275	275	384 450
14	(17, 18]	427	604	1 404	276	276	387 504
15	(18, 19]	350	450	1 250	238	238	297 500
16	(19, 20]	324	398	1 198	225	225	269 550
17	(20, 21]	305	360	1 160	215	215	249 400
18	(21, 22]	268	286	1 086	197	197	213 942
19	(22, 23]	223	196	996	174	174	173 304
20	(23, 24]	161	72	872	143	143	124 696
21	(24, 25]	152	-742	58	0	337	0
22	(25, 26]	130	-776	24	0	324	0
23	(26, 27]	93	-727	73	0	275	0
24	(27, 28]	74	-102	698	100	100	69 800
25	(28, 29]	50	-150	650	88	88	57 200
26	(29, 30]	31	-188	612	78	78	47 736
27	(30, 36]	83	-84	716	104	104	74 464

下载: 导出CSV 

| 显示表格

(2) 假设k_i恒定, 取其为-0.5, 求解结果见表 7。此假设下的航次总收入为5 556 597 USD, 也高于原先的5 108 000 USD, 但较k_i为-0.25时低, 说明k_i的取值对最优总收入有影响。

表  7  试验2的优化结果

Table  7.  Optimizing results of test 2

i	质量区间/t	原托运量/TEU	每标准箱价格变动/USD	每标准箱变动后价格/USD	实际载运量/TEU	变动后托运量/TEU	变动后收入/USD
1	(0, 5]	474	241	1 041	353	353	367 473
2	(5, 6]	259	47	847	235	235	199 045
3	(6, 7]	267	62	862	236	236	203 432
4	(7, 8]	313	115	915	256	256	234 240
5	(8, 9]	308	117	917	250	250	229 250
6	(9, 10]	381	197	997	283	283	282 151
7	(10, 11]	421	244	1 044	299	299	312 156
8	(11, 12]	389	219	1 019	280	280	285 320
9	(12, 13]	450	287	1 087	307	307	333 709
10	(13, 14]	441	285	1 085	299	299	324 415
11	(14, 15]	457	307	1 107	303	303	335 421
12	(15, 16]	429	286	1 086	286	286	310 596
13	(16, 17]	424	288	1 088	280	280	304 640
14	(17, 18]	427	298	1 098	278	278	305 244
15	(18, 19]	350	228	1 028	236	236	242 608
16	(19, 20]	324	209	1 009	219	219	220 971
17	(20, 21]	305	197	997	207	207	206 379
18	(21, 22]	268	167	967	185	185	178 895
19	(22, 23]	223	129	929	159	159	147 711
20	(23, 24]	161	74	874	124	124	108 376
21	(24, 25]	152	72	872	116	116	101 152
22	(25, 26]	130	57	857	102	102	87 414
23	(26, 27]	93	27	827	80	80	66 160
24	(27, 28]	74	14	814	67	67	54 538
25	(28, 29]	50	-3	797	51	51	40 647
26	(29, 30]	31	-15	785	38	38	29 830
27	(30, 36]	83	62	862	52	52	44 824

下载: 导出CSV 

| 显示表格

(3) 假设k_i恒定, 取为-2, 求解结果见表 8。此假设下的航次总收入为5 480 113 USD, 同样高于原先的5 108 000 USD, 但较k_i为-0.5时低, 进一步表明k_i的取值对最优总收入的影响。

表  8  试验3的优化结果

Table  8.  Optimizing results of test 3

i	质量区间/t	原托运量/TEU	每标准箱价格变动/USD	每标准箱变动后价格/USD	实际载运量/TEU	变动后托运量/TEU	变动后收入/USD
1	(0, 5]	474	-102	698	679	679	473 942
2	(5, 6]	259	-121	679	501	501	340 179
3	(6, 7]	267	-108	692	482	482	333 544
4	(7, 8]	313	-84	716	482	482	345 112
5	(8, 9]	308	-74	726	456	456	331 056
6	(9, 10]	381	-44	756	469	469	354 564
7	(10, 11]	421	-22	778	466	466	362 548
8	(11, 12]	389	-19	781	427	427	333 487
9	(12, 13]	450	8	808	434	434	350 672
10	(13, 14]	441	18	818	406	406	332 108
11	(14, 15]	457	33	833	391	391	325 703
12	(15, 16]	429	38	838	353	353	295 814
13	(16, 17]	424	48	848	328	328	278 144
14	(17, 18]	427	61	861	306	306	263 466
15	(18, 19]	350	53	853	244	244	208 132
16	(19, 20]	324	58	858	208	208	178 464
17	(20, 21]	305	65	865	175	175	151 375
18	(21, 22]	268	67	867	133	133	115 311
19	(22, 23]	223	68	868	87	87	75 516
20	(23, 24]	161	64	864	33	33	28 512
21	(24, 25]	152	73	873	5	5	4 365
22	(25, 26]	130	65	865	0	0	0
23	(26, 27]	93	46	846	0	0	0
24	(27, 28]	74	37	837	0	0	0
25	(28, 29]	50	25	825	0	0	0
26	(29, 30]	31	15	815	0	0	0
27	(30, 36]	83	12	812	0	60	0

下载: 导出CSV 

| 显示表格

同时, 若比较试验1、2、3结果中的具体价格变动, 可以发现, 当k_i的绝对值较小时, 在不少区间甚至可以通过直接提高运价来增加收益, 而随着k_i绝对值的逐渐增大, 较轻箱的新定价明显低于其原先的均一价格。当然, 试验1、2、3中的假设仅作为k_i取值的最简单情况进行分析, 以期获得相关基本结论, 实际业务中并不太会出现这样的情况。

(4) 假设k_i非恒定值, 取值见表 9, 其整体趋势见图 2, 即k_i绝对值的取值随i的变化渐小, 其拟合曲线总体呈上凸形态。此假设下的优化结果见表 10。此假设下的航次总收入为6 069 661 USD, 高于原先的5 108 000 USD, 箱位利用率也有明显上升, 达97.55%。

表  9  试验4的k_i值

Table  9.  Values of k_iin test 4

i	ki		i	ki		i	ki
1	-3.82		10	-1.75		19	-0.49
2	-3.55		11	-1.57		20	-0.40
3	-3.29		12	-1.40		21	-0.32
4	-3.04		13	-1.24		22	-0.25
5	-2.80		14	-1.09		23	-0.19
6	-2.57		15	-0.95		24	-0.14
7	-2.35		16	-0.82		25	-0.10
8	-2.14		17	-0.70		26	-0.07
9	-1.94		18	-0.59		27	-0.05

下载: 导出CSV 

| 显示表格

图  2  试验4的k_i变化

Figure  2.  Changes of k_i in test 4

下载: 全尺寸图片 幻灯片

表  10  试验4的优化结果

Table  10.  Optimizing results of test 4

i	质量区间/t	ki	原托运量/TEU	每标准箱价格变动/USD	每标准箱变动后价格/USD	实际载运量/TEU	变动后托运量/TEU	变动后收入/USD
1	(0, 5]	-3.82	474	-156	644	1 070	1 070	689 080
2	(5, 6]	-3.55	259	-143	657	767	767	503 919
3	(6, 7]	-3.29	267	-126	674	682	682	459 668
4	(7, 8]	-3.04	313	-103	698	625	625	436 250
5	(8, 9]	-2.80	308	-86	714	549	549	391 986
6	(9, 10]	-2.57	381	-54	746	521	521	386 666
7	(10, 11]	-2.35	421	-26	774	482	482	373 068
8	(11, 12]	-2.14	389	-12	788	414	414	326 232
9	(12, 13]	-1.94	450	26	826	400	400	330 400
10	(13, 14]	-1.75	441	49	849	356	356	302 244
11	(14, 15]	-1.57	457	81	881	330	330	290 730
12	(15, 16]	-1.40	429	102	902	287	287	258 874
13	(16, 17]	-1.24	424	132	932	260	260	242 320
14	(17, 18]	-1.09	427	170	970	242	242	234 740
15	(18, 19]	-0.95	350	171	971	188	187	182 548
16	(19, 20]	-0.82	324	197	997	162	162	161 514
17	(20, 21]	-0.70	305	230	1 030	144	144	148 320
18	(21, 22]	-0.59	268	252	1 052	119	119	125 188
19	(22, 23]	-0.49	223	266	1 066	93	93	99 138
20	(23, 24]	-0.40	161	252	1 052	60	60	63 120
21	(24, 25]	-0.32	152	301	1 101	56	56	61 656
22	(25, 26]	-0.25	130	72	872	0	112	0
23	(26, 27]	-0.19	93	62	862	0	81	0
24	(27, 28]	-0.14	74	56	856	0	66	0
25	(28, 29]	-0.10	50	49	849	0	45	0
26	(29, 30]	-0.07	31	42	842	0	28	0
27	(30, 36]	-0.05	83	32	832	0	81	0

下载: 导出CSV 

| 显示表格

(5) 假设k_i非恒定值, 取值见表 11, 其整体趋势见图 3, 即k_i绝对值的取值随i的变化渐小, 但其拟合曲线总体呈下凸形态。此假设下的优化结果见表 12。此假设下的航次总收入为6 002 043 USD, 高于原先的5 108 000 USD, 箱位利用率达100%。但总体看来, 试验5与试验4优化结果的差异并不大, 这表明只要k_i的总体变化趋势相近, k_i的实际具体取值与形态对优化结果影响不大。

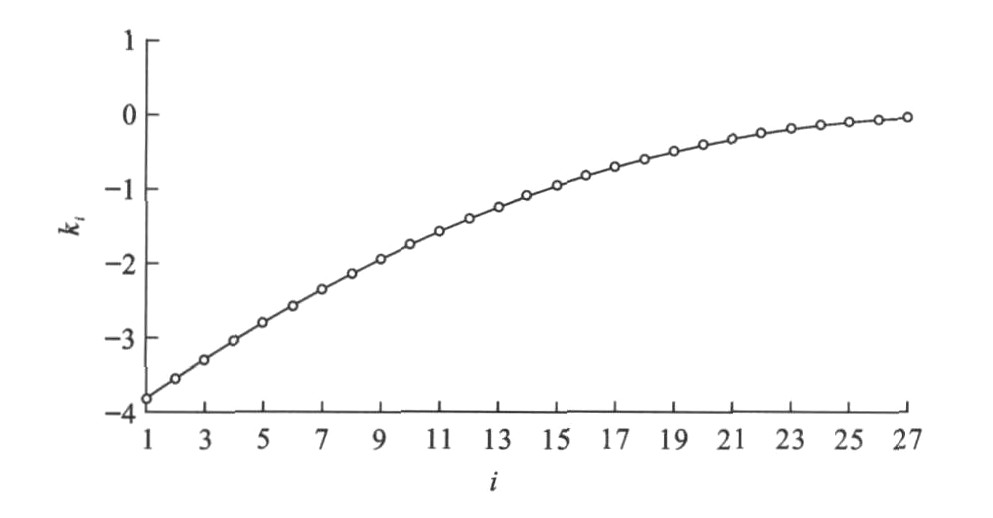
表  11  试验5的k_i值

Table  11.  Values of k_iin test 5

i	ki		i	ki		i	ki
1	-3.82		10	-3.28		19	-1.93
2	-3.80		11	-3.17		20	-1.73
3	-3.77		12	-3.05		21	-1.52
4	-3.73		13	-2.92		22	-1.30
5	-3.68		14	-2.78		23	-1.07
6	-3.62		15	-2.63		24	-0.83
7	-3.55		16	-2.47		25	-0.58
8	-3.47		17	-2.30		26	-0.32
9	-3.38		18	-2.12		27	-0.05

下载: 导出CSV 

| 显示表格

图  3  试验5的k_i变化

Figure  3.  Changes of k_i in test 5

下载: 全尺寸图片 幻灯片

表  12  试验5的优化结果

Table  12.  Optimizing results of test 5

i	质量区间/t	ki	原托运量/TEU	每标准箱价格变动/USD	每标准箱变动后价格/USD	实际载运量/TEU	变动后托运量/TEU	变动后收入/USD
1	(0, 5]	-3.82	474	-134	666	985	985	656 010
2	(5, 6]	-3.80	259	-125	675	736	736	496 800
3	(6, 7]	-3.77	267	-112	688	689	689	474 032
4	(7, 8]	-3.73	313	-93	707	661	661	467 327
5	(8, 9]	-3.68	308	-81	719	607	607	436 433
6	(9, 10]	-3.62	381	-58	742	593	593	440 006
7	(10, 11]	-3.55	421	-40	760	562	562	427 120
8	(11, 12]	-3.47	389	-31	769	496	496	381 424
9	(12, 13]	-3.38	450	-8	792	478	478	378 576
10	(13, 14]	-3.28	441	5	805	426	426	342 930
11	(14, 15]	-3.17	457	21	821	389	389	319 369
12	(15, 16]	-3.05	429	32	832	332	332	276 224
13	(16, 17]	-2.92	424	46	846	289	289	244 494
14	(17, 18]	-2.78	427	62	862	253	253	218 086
15	(18, 19]	-2.63	350	64	864	181	181	156 384
16	(19, 20]	-2.47	324	75	875	138	138	120 750
17	(20, 21]	-2.30	305	88	888	102	102	90 576
18	(21, 22]	-2.12	268	97	897	62	62	55 614
19	(22, 23]	-1.93	223	104	904	22	22	19 888
20	(23, 24]	-1.73	161	93	893	0	0	0
21	(24, 25]	-1.52	152	100	900	0	0	0
22	(25, 26]	-1.30	130	100	900	0	0	0
23	(26, 27]	-1.07	93	87	887	0	0	0
24	(27, 28]	-0.83	74	89	889	0	0	0
25	(28, 29]	-0.58	50	86	886	0	0	0
26	(29, 30]	-0.32	31	97	897	0	0	0
27	(30, 36]	-0.05	83	-5	795	0	83	0

下载: 导出CSV 

| 显示表格

同时需要说明的是, 考虑到各承运人接收偏重箱托运的客观“偏好”, k_i绝对值的取值随i的变化渐大的情况在实践不会出现, 因此本文不再赘述。

至此可以发现, k_i具体取值的不同会对最优值产生一定影响, 但无论k_i取值符合何种规律, 有一点是确定的, 即采用等级定价的方式总能获得比原先均一定价方式下更优的收益。

此外, 上述5种假设的试验结果还有一个共同点, 即对于向其托运的较轻箱, 承运人均应尽可能多接运, 以拉低其所运集装箱的平均质量, 为承运单位运价较高的“偏重箱”腾出载重吨指标的空间, 这也比较符合目前业务实践的客观规律。

集装箱班轮公司在对外公布运价时, 可采用前文所述的“基本运费+偏重箱附加费”方式。若采用数学试验所选取的频度区间, 则以单箱折算质量5 t作为基本运费的基准质量, 随着集装箱单箱折算质量的上升, 收取对应的“偏重箱附加费”。

以表 12为例, 若k_i取值符合试验5的假设, 则实际对货主公布的二部定价可以制成表 13的形式。对货主而言, 这样的一种二部定价形式也要比原先均一定价更为公平合理, 也比较接近班轮运价本的传统形式。通过表 13可以发现, 尽管以单箱折算质量5 t作为基本运费的基准质量, 但实际上, 直至(12, 13]区间, 新运价都较原均一运价低, 也从另一侧面验证了模型的合理性。

表  13  二部定价运价

Table  13.  Freights of two-part pricing

i	质量区间/t	基本运费率/ (USD·TEU-1)	偏重箱附加费率/ (USD·TEU-1)	总运费/USD
1	(0, 5]	666	—	666
2	(5, 6]	666	9	675
3	(6, 7]	666	22	688
4	(7, 8]	666	41	707
5	(8, 9]	666	53	719
6	(9, 10]	666	76	742
7	(10, 11]	666	94	760
8	(11, 12]	666	103	769
9	(12, 13]	666	126	792
10	(13, 14]	666	139	805
11	(14, 15]	666	155	821
12	(15, 16]	666	166	832
13	(16, 17]	666	180	846
14	(17, 18]	666	196	862
15	(18, 19]	666	198	864
16	(19, 20]	666	209	875
17	(20, 21]	666	222	888
18	(21, 22]	666	231	897
19	(22, 23]	666	238	904
20	(23, 24]	666	227	893
21	(24, 25]	666	234	900
22	(25, 26]	666	234	900
23	(26, 27]	666	221	887
24	(27, 28]	666	223	889
25	(28, 29]	666	220	886
26	(29, 30]	666	231	897
27	(30, 36]	666	129	795

下载: 导出CSV 

| 显示表格

本文在进行数学试验时所取的首区间为(0, 5], 如果选择(0, 10]作为首区间, 则相应求得的优化结论相仿, 但最优值会略小于前者。同时, 如果集装箱班轮公司选择(0, 10]作为优化求解的首区间, 则其在公布运价时, 基本运费的基准点则需相应改为单箱总质量10 t, 定价公布形式与表 13相同。

5.   结语

本文以二部定价理论为出发点, 基于对典型数据严谨的统计学分析, 首次建立了针对该问题的二部定价优化模型, 并通过算例分析, 说明了若集装箱班轮运输企业采用质量等级二部非线性定价方法, 既可以提高其船舶载运能力的利用率, 更能由此实现其收益水平的全面提升。文章还给出了二部定价形式的质量等级运价表, 该运价表形式的合理性与可操作性得到来自企业的较高评价。

当然, 为阐明研究的主旨, 本文仅随机选取了某企业在某港口的某具有代表性航次接受托运的集装箱质量数据进行了分析。同时, 本文对ΔP_i与ΔQ_i之间的映射关系V_i也只是进行了最为简化的假设, 本文所研究的理论在投入实际应用的过程中, 相关运输企业还需开展大量的统计分析工作, 以尽可能精确地确定ΔP_i与ΔQ_i之间的映射关系。

本文推导出的相关统计学结论可作为该问题后续研究的基础, 而基于本文建立的优化模型, 后续研究则可在复杂的单箱总质量分布及复杂的ΔP_i与ΔQ_i映射关系方面作进一步的加强与完善。