Airport delay performance evaluation based on fuzzy linear regression model
Article Text (Baidu Translation)
-
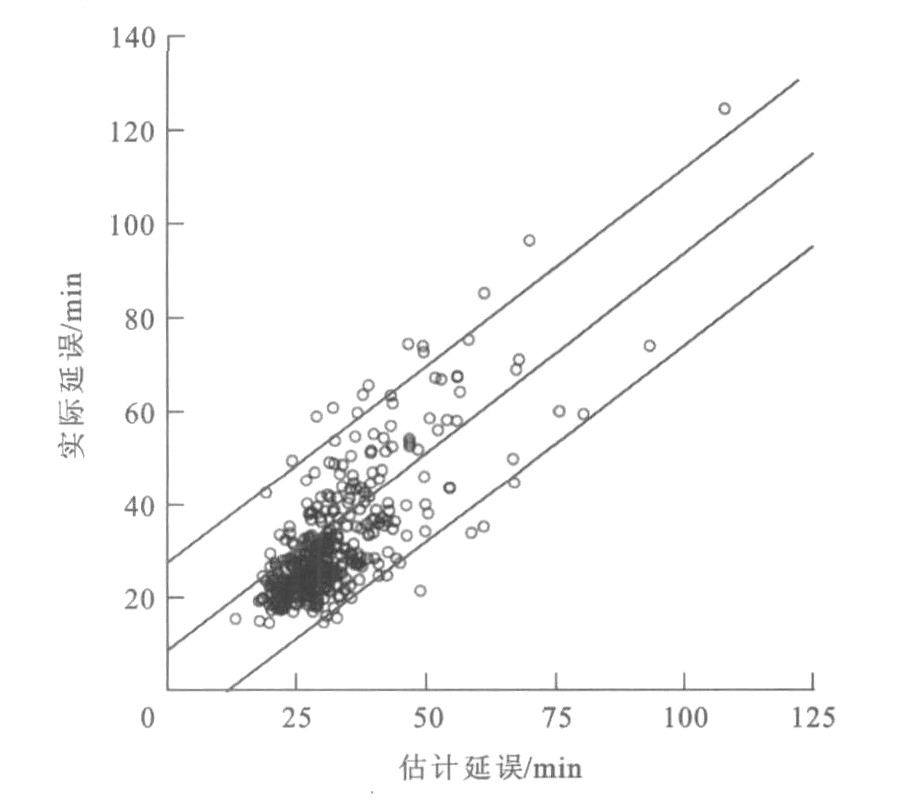
摘要: 为了有效评估机场延误性能, 考虑到天气和交通变量取值通常会受到一些不确定性因素的影响, 建立了机场到达延误与天气和交通需求之间的模糊线性回归模型。根据模糊线性回归模型得到了估计延误, 通过比较估计延误与实际延误, 可以得到评估延误的连续型性能基准, 并根据性能基准对延误性能进行评估。研究结果表明: 机场到达延误与天气和交通需求之间有较强的线性关系, 可以用线性模型进行拟合。得到的延误性能基准同时考虑了机场天气和交通需求对延误的影响, 将机场到达延误分为低、中、高三种水平, 从而可对不同日的延误水平进行比较评估。Abstract: In order to effectively evaluate the delay performance of airport, taking into account that the weather and traffic variable values were usually subject to some uncertainty factors, the features of traffic demand and weather were used to develop a fuzzy linear regression model for airport arrival delay, and the estimated delay was computed.The continuous baseline to measure operational airport delay performance was obtained by comparing estimated delay with actual delay.The delay performance could be evaluated based on the delay baseline.Analysis result indicates that the features of traffic demand and weather have a strong linear relationship with airport arrival delay, which can be fitted with the model.The delay performance baseline takes into account the impact of airport weather and traffic demand on the delay, and divides the delay into low, medium and high levels, and the delays of different days can be compared and evaluated.
-
表 1 模糊线性回归模型的验证
Table 1. Validation of fuzzy linear regression model
序号 yi xi1 xi2 xi3 yi* Ω/% 1 32.60 1 162 11 8.00 30.61 6 2 30.64 1 176 15 8.00 31.17 2 3 36.34 1 178 15 11.10 36.11 1 4 28.39 1 172 13 9.90 33.94 20 5 34.15 1 174 19 12.00 37.83 11 6 57.60 1 167 68 18.10 51.71 10 7 33.01 1 168 23 8.90 33.18 1 8 36.10 1 174 16 7.00 29.64 18 9 29.00 1 170 8 8.00 30.46 5 10 29.48 1 142 12 8.90 31.83 8 11 31.49 1 176 13 8.90 32.42 3 12 25.37 1 168 14 7.00 29.38 16 13 27.99 1 168 6 7.00 28.67 2 14 26.17 1 176 11 8.00 30.81 18 15 37.71 1 167 48 8.90 35.37 6 16 35.05 1 133 7 8.90 31.26 11 17 37.53 1 139 5 12.00 36.08 4 18 43.05 1 156 24 12.00 38.00 12 19 45.74 1 158 40 15.00 44.20 3 20 63.79 1 171 105 20.00 58.05 9 21 44.33 1 117 73 18.10 51.42 16 22 44.44 1 136 71 14.00 45.03 1 23 28.87 1 171 8 8.00 30.48 6 24 28.31 1 161 18 8.90 32.64 15 25 36.21 1 161 25 7.00 30.25 16 26 42.23 1 147 32 13.00 40.16 5 27 35.26 1 137 22 13.00 39.13 11 28 34.27 1 142 18 13.00 38.85 13 29 138.23 1 067 926 19.00 127.44 8 30 85.09 1 114 435 13.00 75.27 12 31 37.13 1 200 90 11.10 43.05 16 -
[1] 胡明华, 徐肖豪, 陈爱民, 等. 空中交通流量管理中的多元受限地面等待策略问题研究[J]. 航空学报, 1998, 19(1): 78-82. doi: 10.3321/j.issn:1000-6893.1998.01.016HU Ming-hua, XU Xiao-hao, CHEN Ai-min, et al. Multiple unit ground holding strategy problem research in air traffic flow management[J]. Acta Aeronautica et AstronauticaSinica, 1998, 19(1): 78-82. (in Chinese) doi: 10.3321/j.issn:1000-6893.1998.01.016 [2] 罗喜伶, 张其善. 起降容量受限的地面等待模型研究[J]. 北京航空航天大学学报, 2004, 30(2): 127-130. https://www.cnki.com.cn/Article/CJFDTOTAL-BJHK200402007.htmLUO Xi-ling, ZHANG Qi-shan. Research on GHP model with constrained departing and landing capacities[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(2): 127-130. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJHK200402007.htm [3] 王来军, 史忠科, 荣群山. 空中交通管理中的地面等待策略研究[J]. 数学的实践与认识, 2004, 34(11): 39-46. doi: 10.3969/j.issn.1000-0984.2004.11.008WANG Lai-jun, SHI Zhong-ke, RONG Qun-shan. General research on ground holding policy in air traffic management[J]. Mathematicsin Practice and Theory, 2004, 34(11): 39-46. (in Chinese) doi: 10.3969/j.issn.1000-0984.2004.11.008 [4] GILBO E P. Optimizing airport capacity utilization in air traffic flow management subject to constraints at arrival and departure fixes[J]. IEEE Transactions on Control Systems Technology, 1997, 5(5): 490-503. doi: 10.1109/87.623035 [5] 王飞, 徐肖豪, 张静. 终端区飞机排序的混合人工鱼群算法[J]. 交通运输工程学报, 2008, 8(3): 68-72. doi: 10.3321/j.issn:1671-1637.2008.03.015WANG Fei, XU Xiao-hao, ZHANG Jing. Mixed artificial fish school algorithmof aircraft sequencing in terminal area[J]. Journal of Traffic and Transportation Engineering, 2008, 8(3): 68-72. (in Chinese) doi: 10.3321/j.issn:1671-1637.2008.03.015 [6] KROZEL J, CAPOZZI B, ANDRE A D, et al. The future national airspace system: design requirements imposed by weather constraints[C]//AIAA. Proceedings of AIAA Guidance, Navigation and Control Conference. Austin: AIAA, 2003: 1-14. [7] MUELLER E R, CHATTERJI G B. Analysis of aircraft arrival and departure delay characteristics[C]//AIAA. Proceedings of AIAA's Aircraft Technology, Integration and Operations. Los Angeles: AIAA, 2002: 1-14. [8] KROZEL J, HOFFMAN B, PENNY S, et al. Selection of datasets for NAS-wide simulation validations[R]. Herndon: Metron Aviation, 2002. [9] KROZEL J, HOFFEMAN B, PENNY S, et al. Aggregate statistics of the national airspace system[C]//AIAA. Proceedings of AIAA Guidance, Navigation, and Control Conference. Austin: AIAA, 2003: 15-29. [10] CALLAHAM MB, DEARMON J S, COOPER A M, et al. Assessing NAS performance: normalizing for the effects of weather[C]//FAA, Eurocontrol. Proceedings of the 4th USA/Europe Air Traffic Management R & D Seminars. Santa Fe: FAA, Eurocontrol, 2001: 1-11. [11] CHATTERJI G B, SRIDHAR B. National airspace system delay estimation using weather weighted traffic counts[C]//AIAA. AIAA Guidance, Navigation and Control Conference Exhibit. San Francisco: AI AA, 2005: 1-17. [12] ABDEL-ATY M, LEE C, BAI Yu-qiong, et al. Detecting periodic patterns of arrival delay[J]. Journal of Air Transport Management, 2007, 13(6): 355-361. doi: 10.1016/j.jairtraman.2007.06.002 [13] XU Ning, LASKEY K B, CHEN C H, et al. Bayesian network analysis of flight delays[C]//TRB. TRB 2007 Annual Meeting. Washington DC: TRB, 2007: 1-12. [14] MUKHERJEE A, LOVELL D J, BALL M O, et al. Modeling delays and cancellation probabilities to support strategic simulations[C]//FAA, Eurocontrol. Proceedings of the 6th USA/Europe Air Traffic Management R & D Seminar. Baltimore: FAA, Eurocontrol, 2005: 1-10. [15] 徐涛, 丁建立, 顾彬, 等. 基于增量式排列支持向量机的机场航班延误预警[J]. 航空学报, 2009, 30(7): 1256-1263. doi: 10.3321/j.issn:1000-6893.2009.07.014XU Tao, DING Jian-li, GU Bin, et al. Forecast warning level of flight delays based on incremental ranking support vector machine[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7): 1256-1263. (in Chinese) doi: 10.3321/j.issn:1000-6893.2009.07.014 [16] 袁瑗, 陈兵, 徐涛, 等. 基于先验知识的多类CVM航班延误预警模型[J]. 吉林大学学报: 工学版, 2010, 40(3): 752-757. https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201003031.htmYUAN Yuan, CHEN Bing, XU Tao, et al. Prior knowledge based multi-class core vector machine for flight delay early warning[J]. Journal of Jilin University: Engineering and Technology Edition, 2010, 40(3): 752-757. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201003031.htm [17] KIVESTU P A. Alternative methods of investigating the time dependent M/G/K queue[D]. Cambridge: Massachusetts Institute of Technology, 1976. [18] MALONE K M. Dynamic queueing systems: behavior and approximations for individual queues and networks[D]. Cambridge: Massachusetts Institute of Technology, 1995. [19] 吴冲, 潘启树, 李汉铃. 模糊线性回归预测[J]. 西安交通大学学报, 2000, 34(9): 100-102. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJT200009025.htmWU Chong, PAN Qi-shu, LI Han-ling. Fuzzy linear regression prediction[J]. Journal of Xi'an Jiaotong University, 2000, 34(9): 100-102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJT200009025.htm [20] 耿光飞, 郭喜庆. 模糊线性回归法在负荷预测中的应用[J]. 电网技术, 2002, 26(4): 19-21. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200204004.htmGENG Guang-fei, GUO Xi-qing. Application of fuzzy linear regression to load forecasting[J]. Power System Technology, 2002, 26(4): 19-21. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200204004.htm [21] 景英川. 模糊线性回归模型中的拟合度问题[J]. 山西师范大学学报: 自然科学版, 2002, 16(3): 10-14. https://www.cnki.com.cn/Article/CJFDTOTAL-SFDX200203003.htmJING Ying-chuan. Imitation degree problemin fuzzy linear regression model[J]. Journal of Shanxi Teacher's University: Natural Science Edition, 2002, 16(3): 10-14. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFDX200203003.htm -





 下载:
下载: