Numerical simulation of biaxial test for granular materials based on discrete element method
-
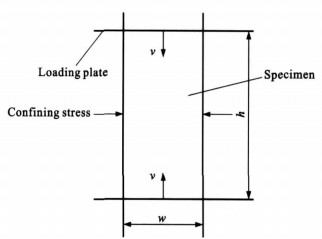
摘要: 为了得到颗粒材料的力学参数与试验条件之间的关系, 选取5组粒径范围的颗粒材料, 利用离散元方法生成初始试件, 并数值模拟了其双轴试验, 分析了不同围压对材料弹性模量和强度的影响, 以及不同加载速率下材料的弹性模量、泊松比和强度的变化规律。提取了围压为10MPa与加载速率为0.03m.s-1时5组试件的应力-应变曲线, 从微观角度给出了荷载作用后试件中的裂缝分布。模拟结果表明: 随着围压的增大, 5组试件的弹性模量和强度增大, 增长趋势相对平缓, 但粒径为9.50~13.20mm的试件出现较大波动; 加载速率与弹性模量、泊松比、强度和裂缝初始应力基本呈二次多项式关系, 最小判定系数为0.9009, 最大为0.9959;在5组试件中, 随着粒径的增大, 由应力-应变曲线得到的应力峰值减小。Abstract: In order to obtain the relationships between the mechanics parameters of granular materials and test conditions, discrete element method(DEM)was applied to prepare the initial specimens and simulate the biaxial test of granular materials with five particle diameters.The influences of different confining pressures on the elastic moduli, the strengths and the variation rules of elastic moduli, the Poisson's ratios and the strengths under different loading velocities were analyzed.The stress-strain curves of five specimens were plotted under confining pressure of 10 MPa and loading velocity of 0.03 m·s-1, and the crack distributions in the specimens were also given from microscopic viewpoint.Simulated result indicates that the elastic moduli and strengths of five specimens increase with confining pressures, and the increasing trends are relatively smooth.However, the specimen with 9.50~13.20 mm particles has a bigger fluctuation.The relationships between loading velocity and the elastic modulus, the Poisson's ratio, the strength and the crack-initiation stress are quadratic polynomials basically, the minimum correlation coefficient is 0.900 9, and the maximum correlation coefficient is 0.995 9.In addition, the peak values of stresses obtained from stress-strain curves reduce with the increase of particle diameters.
-
Key words:
- pavement material /
- granular material /
- mechanics parameters /
- biaxial test /
- discrete element method
-
Table 1. Model parameters of biaxial test

Table 2. Particle parameters

-
[1] DU Shun-cheng, DAI Jing-liang. Multilevel anti-shear grading design method based on theory of granular material mechanics[J]. China Journal of Highway and Transport, 2008, 21(1): 35-39. (in Chinese) [2] KIM J, WEST R C. Application of the viscoelastic continuum damage model to the indirect tension test at a single temperature[J]. Journal of Engineering Mechanics, 2010, 136(4): 496-505. doi: 10.1061/(ASCE)EM.1943-7889.0000094 [3] FROST J D, EVANS T M. Membrane effects in biaxial compression tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(7): 986-991. doi: 10.1061/(ASCE)GT.1943-5606.0000011 [4] TEUNISSEN J A M. Shear band analysis in the biaxial test[J]. International Journal of Geomechanics, 2008, 8(5): 311-321. doi: 10.1061/(ASCE)1532-3641(2008)8:5(311) [5] CEDOLIN L, MULAS M G. Biaxial stress-strain relation for concrete[J]. Journal of Engineering Mechanics, 1984, 110(2): 187-206. doi: 10.1061/(ASCE)0733-9399(1984)110:2(187) [6] JIANG Ming-jing, LI Xiu-mei, SUN Yu-gang, et al. Discrete element simulation of biaxial compression test considering rolling resistance[J]. Rock and Soil Mechanics, 2009, 30(S2): 514-517. (in Chinese) [7] ZHANG Chong, SHU Gan-ping. Effect of particle shape on biaxial tests simulated by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(8): 1281-1286. (in Chinese) [8] ZHOU Jian, CHI Yu-wei, CHI Yong, et al. Simulation of biaxial test on sand by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(6): 701-704. (in Chinese) [9] YE Yong, XU Xi-peng. Study on distinct element modeling method of rock-like brittleness material[J]. Journal of Zhengzhou University of Light Industry: Natural Science, 2008, 23(5): 62-66. (in Chinese) [10] LU Pei-yin. Experimental study on dynamic strength and deformation of concrete under uniaxial and biaxial action[D]. Dalian: Dalian University of Technology, 2001. (in Chinese) -





 下载:
下载: