Dual-objective reliable network design based on particle swarm optimization
-
摘要: 用离散的路段通行能力变量来刻画路网的随机性, 建立了网络设计的双层规划模型。上层模型为基于路网期望总走行时间最小和路网净经济效益可靠度最大的双目标规划模型, 下层模型为弹性需求下的用户平衡配流模型。采用增设多余需求路段的方法求解下层模型, 采用基于向量的粒子群算法(VEPSO)求解整个双层规划模型。计算结果表明: 所得到的解为一组Pareto解, 路网期望总走行时间和净经济效益可靠性为2个相悖目标; 随着期望总走行时间下降, 可靠度也有所降低; 在可靠度不变的情况下, 减少期望总走行时间, 会导致总投资额的增加。在进行网络设计时, 应结合总投资额和现实需要来选取最优解作为网络设计方案。Abstract: A bi-level programming model of network design was established by supposing the capability of road section to be a discrete random variable. The upper model was a dual-objective programming model, which considered the minimum of network expected travel time and the maximum of network net ecoromic benefit reliability. The lower model was a user equilibrium(UE)with elastic demand. The excess-demand formulation was adopted to solve the lower model, and the vector evaluated particle swarm optimization(VEPSO)was adopted to solve the whole bi-level programming. Analysis result indicates that the outcome is a group of Pareto solutions, network expected travel time and network net economic benefit reliability are contradicting objectives. Network expected travel time decreases, the reliability also decreases. When the reliability keeps invariant, total investment amount increases with the decrease of expected travel time. The optimum scheme for network design should be chosen by combining total investment amount with actual situation.
-
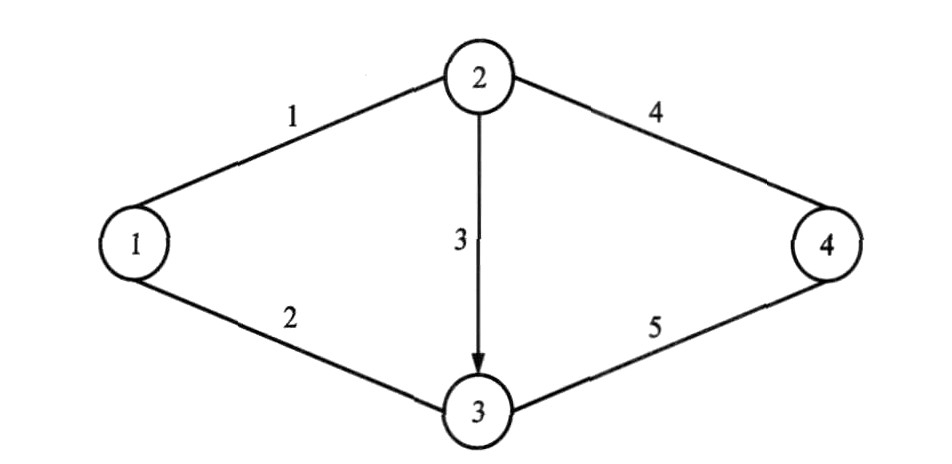
表 1 网络参数
Table 1. Network parameters
路段编号 t β ua qal pal 1 5 40 1.0 0.20 0.7 0.80 2 4 40 1.0 0.30 0.6 0.70 3 2 80 3 15 1.0 0.25 0.8 0.75 4 5 20 1.0 0.10 0.7 0.90 5 3 40 7 10 1.0 0.15 0.8 0.85 表 2 计算结果
Table 2. Computational results
解的编号 路段编号 设计通行能力增加值 路网期望总走行时间 路网可靠度 总投资额 1 3 8.142 1 512.7 0.82 210.23 5 1.274 2 3 7.171 1 482.8 0.78 225.22 5 3.183 3 3 4.885 1 454.0 0.78 258.10 5 5.162 -
[1] DI MITRIOU L, STATHOPOULOS A, TSEKRIS T. Reliable stochastic design of road network system[J]. International Journalof Industrial and Systems Engineering, 2008, 3(5): 549-574. doi: 10.1504/IJISE.2008.018232 [2] 许良, 高自友. 基于路段能力可靠性的城市交通网络设计[J]. 中国公路学报, 2006, 19(2): 86-90. doi: 10.3321/j.issn:1001-7372.2006.02.015XU Liang, GAO Zi-you. Urban transport network design based on link capacity reliability[J]. China Journal of High-way and Transport, 2006, 19(2): 86-90. (in Chinese) doi: 10.3321/j.issn:1001-7372.2006.02.015 [3] 许良, 高自友. 基于出行时间可靠性的城市交通网络设计[J]. 系统仿真学报, 2008, 20(2): 494-498. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200802054.htmXU Liang, GAO Zi-you. Urban transportation network design based on travel time reliability[J]. Journal of System Simula-tion, 2008, 20(2): 494-498. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200802054.htm [4] LO H K, TUNG Y K. Network with degradable links: capacity analysis and design[J]. Transportation Research Part B: Methodological, 2003, 37(4): 345-363. doi: 10.1016/S0191-2615(02)00017-6 [5] 刘海旭, 蒲云. 弹性需求随机路网的可靠性[J]. 公路交通科技, 2005, 22(7): 97-100. doi: 10.3969/j.issn.1002-0268.2005.07.025LI U Hai-xu, PU Yun. Reliability of stochastic road network with elastic demand[J]. Journal of Highway and Transporta-tion Research and Development, 2005, 22(7): 97-100. (in Chinese) doi: 10.3969/j.issn.1002-0268.2005.07.025 [6] YANG Hai, HUANG Hai-jun. Principle of marginal-cost pricing: how does it work in a general road network-[J]. Transportation Research Part A: Policy and Practice, 1998, 32(1): 45-54. doi: 10.1016/S0965-8564(97)00018-9 [7] GERSHWI N S B, TAN H N. Hybrid optimization: optimal static traffic control constrained by drivers'route choice behavior[R]. Cambridge: Massachusetts Institute of Tech-nology, 1978. [8] CHIOUS W. Bilevel programming for the continuous trans-port network design problem[J]. Transportation Research Part B: Methodological, 2005, 39(4): 361-383. doi: 10.1016/S0191-2615(04)00085-2 [9] SUH S, KI M T J. Solving nonlinear bilevel programming models of the equilibriumnetwork design problem: a compara-tive review[J]. Annals of Operations Research, 1992, 34(1): 203-218. doi: 10.1007/BF02098180 [10] GARTNER N H. Optimal traffic assignment with elastic demands: a reviewpartⅡalgorithmic approaches[J]. Trans-portation Science, 1980, 14(2): 192-208. doi: 10.1287/trsc.14.2.192 [11] WAKABAYASHI H, IIDA Y. Upper and lower bounds of terminal reliability of road networks: an efficient method with boolean algebra[J]. Journal of Nature Disaster Science, 1992, 14(1): 29-44. [12] YANG C L, KUBAT P. Efficient computation of most prob-able states for communication networks with multimode com-ponents[J]. IEEE Transactions on Communications, 1989, 37(5): 535-538. doi: 10.1109/26.24607 [13] PARSOPOULOS K E, VRAHATIS M N. Particle swarm optimization method in multiobjective problems[C]∥ACM Special Interest Group on Applied Computing. Proceeding of the2002ACM Symposium on Applied Computing. Madrid: ACM, 2002: 603-607. -





 下载:
下载: