Longitudinal creep force properties of wheel and rail under short-pitch corrugation state
-
摘要: 为了对具有简谐波形的钢轨短波波磨进行分组与分析轮轨非稳态滚动接触的纵向蠕滑力特性, 引入了波磨深度指数与波长比, 采用Kalker三维滚动接触理论计算了车轮的纵向蠕滑力, 并与采用稳态滚动理论计算结果进行了对比, 使用频率响应的系统辨识法对纵向蠕滑力的波动分量进行了拟合, 在短波波磨等深度指数条件下, 用波长比的二阶传递函数描述了轮轨纵向蠕滑力的波动分量与稳态理论波动分量之间的关系, 使用传递函数, 由稳态纵向蠕滑力的波动分量计算了非稳态纵向蠕滑力的波动分量, 进而计算了非稳态的纵向蠕滑力。计算结果表明: 在小蠕滑条件下, 由Kalker三维滚动接触理论计算出的纵向蠕滑力的波动分量随着波长比的变化产生明显的幅值衰减和相位滞后, 波长比越大, 幅值衰减越大, 相位滞后越多, 而稳态滚动理论的计算结果与波长比无关。由传递函数和Kalker数值理论计算的纵向蠕滑力的时域波形、频域幅值谱和相位谱相同。Abstract: Shallowness factor and wavelength ratio were induced to group sinusoidal short-pitch corrugations with simple harmonic waveforms and to analyze the properties of longitudinal wheel/rail creep forces for unsteady state rolling contact, the longitudinal creep forces due to sinusoidal short-pitch corrugations were calculated by Kalker 3D rolling contact theory, and the calculation result was compared with the calculation result from steady rolling contact theory. The system identification method of frequency response was used to fit the fluctuating part of unsteady longitudinal creep force. The relationship of fluctuating parts for unsteady state and steady state longitudinal creep forces was described as two order transfer function of wavelength ratio when sinusoidal short-pitch corrugations had same shallowness factor. The fluctuating part of unsteady longitudinal creep force was calculated according to the fluctuating part of steady longitudinal creep force, thereout, the unsteady longitudinal creep force was calculated. Calculation result shows that under small creep condition, the fluctuating part of unsteady longitudinal creep force decreases in amplitude and phase lag with the growth of wavelength ratio. The bigger wavelength ratio is, the smaller amplitude is, and the more phase lag is. However, the result from steady state theory is independent of wavelength ratio. For unsteady longitudinal creep forces calculated by the transfer function and Kalker 3D rolling contact theory, the waveforms in time domain, the amplitudes and phase spectrums in frequency domain are accordant.
-
0. 引言
根据波峰间的长度, 钢轨波磨可分为长波波磨和短波波磨等类型, 短波波磨是指波长在20~100 mm之间的钢轨波浪形磨耗, 也称为“响轨”波磨, 短波波磨通常发生在直线、低轴重、高速的线路上[1]。关于短波波磨成因, 存在多种解释, 大多数认为短波波磨与纵向蠕滑力引起的磨耗相关[2-6]。
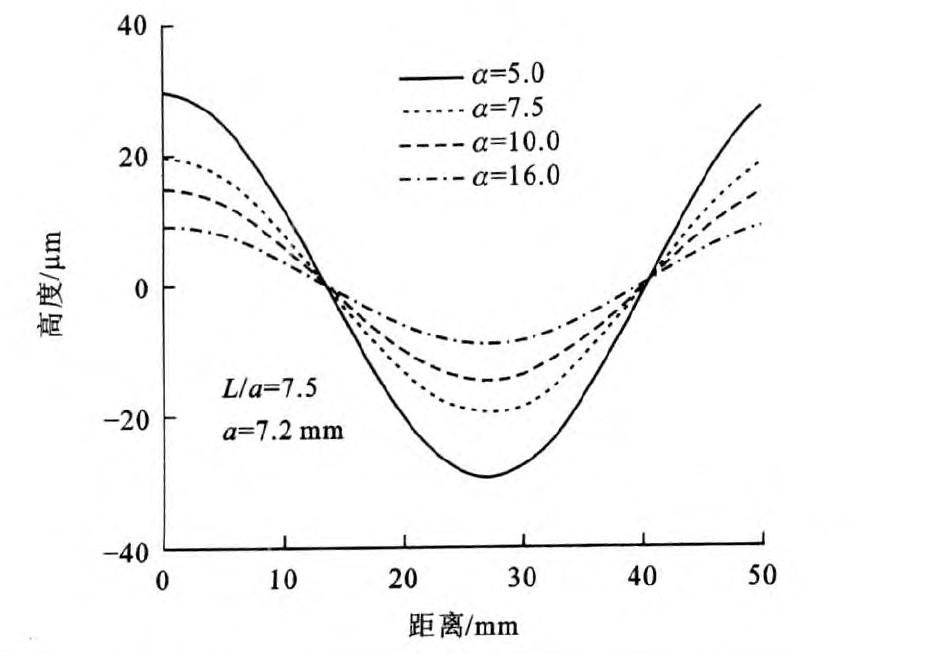
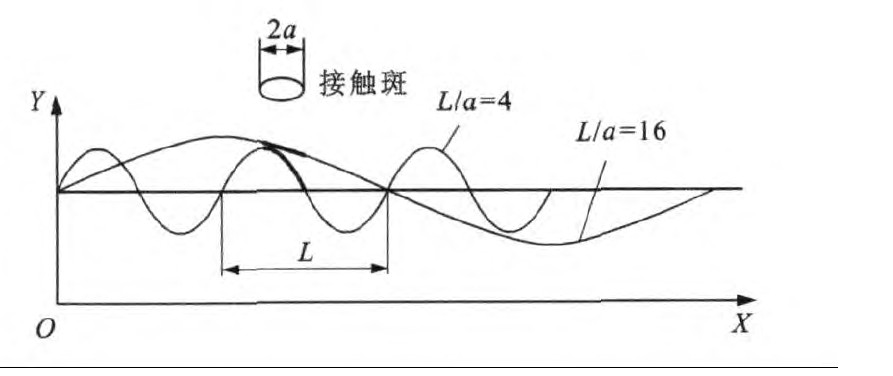
车轮在具有短波波磨的钢轨上滚动, 是一个典型的轮轨非稳态滚动接触问题。与非稳态滚动相对的是稳态滚动, 在稳态滚动过程中, 接触斑的外形和其他参数如蠕滑率与法向力等保持不变。为了衡量接触参数的变化速度, 引入了一个无量纲的波长比L/a, 其中L为接触参数的运动波长(如短波波磨的波长), a为接触斑纵轴直径之半。图 1给出了一个非稳态滚动接触的过程示意, 其中X轴表示接触参数的运动波长, Y轴表示接触参数的变化幅值, L/a=16意味着接触参数的变化是比较缓慢的, 而L/a=4则表示接触参数的变化是快速的。
严格地讲, 铁道车辆的轮轨接触都属于非稳态滚动接触, 但是大多数的铁道车辆动力学现象的非稳态效应非常微弱, 近似于稳态滚动, 使用稳态滚动接触理论能够很好地解释其力学行为。根据Kalker和Gross-Thebing的研究, 当L/a小于10时, 就必须考虑滚动接触的非稳态效应[7]。
Kalker最早开始研究瞬态滚动问题, 分析了车轮从静止到稳态滚动过程中的二维瞬态接触问题[8]; Knothe和Gross-Thebing研究了蠕滑率简谐波动情况下蠕滑力的变化规律, 发现它们之间可以用运动波长和接触斑半轴长之比L/a的传递函数来表达[9-10]; Alonso和Giménez则尝试修改Kalker简化理论来描述非稳态滚动时的蠕滑力[11]。本文的研究发现, 当等深度的短波波磨按照简谐规律波动时, 纵向蠕滑力的波动分量可用短波波磨波长L与接触斑半径a之比的传递函数来描述, 因此, 可以根据传递函数快速计算短波波磨状态的非稳态轮轨纵向蠕滑力。
1. 钢轨波磨深度
假设钢轨短波波磨按照简谐周期变化, 则波磨在距离x处的幅值z为
式中: Z0为波峰高度; φ0为初始相位角。
对于波形复杂的波磨, 可视为多个简谐波磨的组合。为了表示钢轨波磨的深浅程度, 引入波磨深度指数α[12]
式中: Rw为车轮半径。
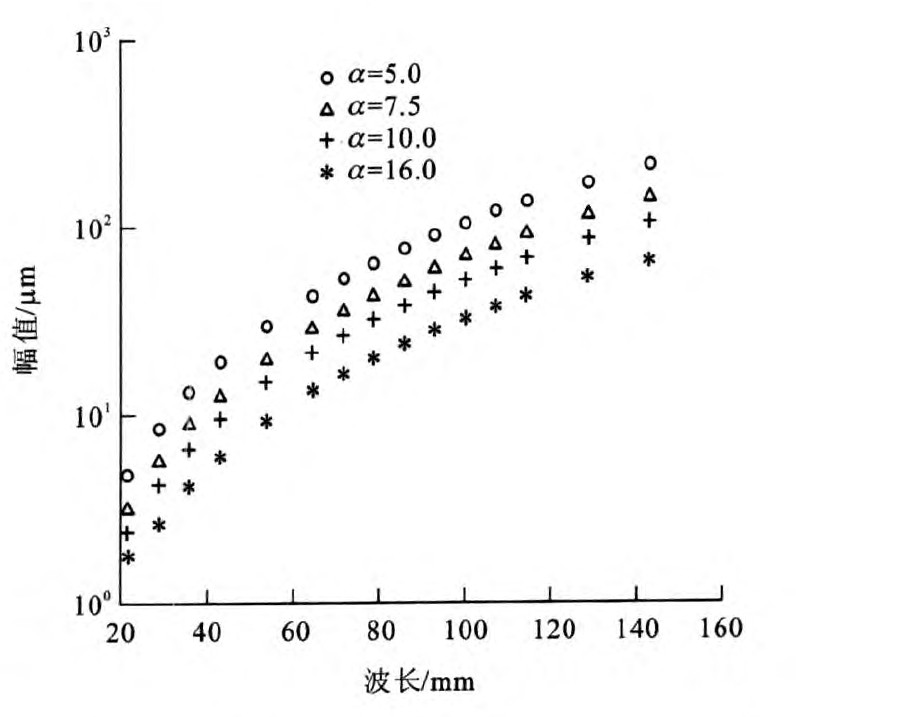
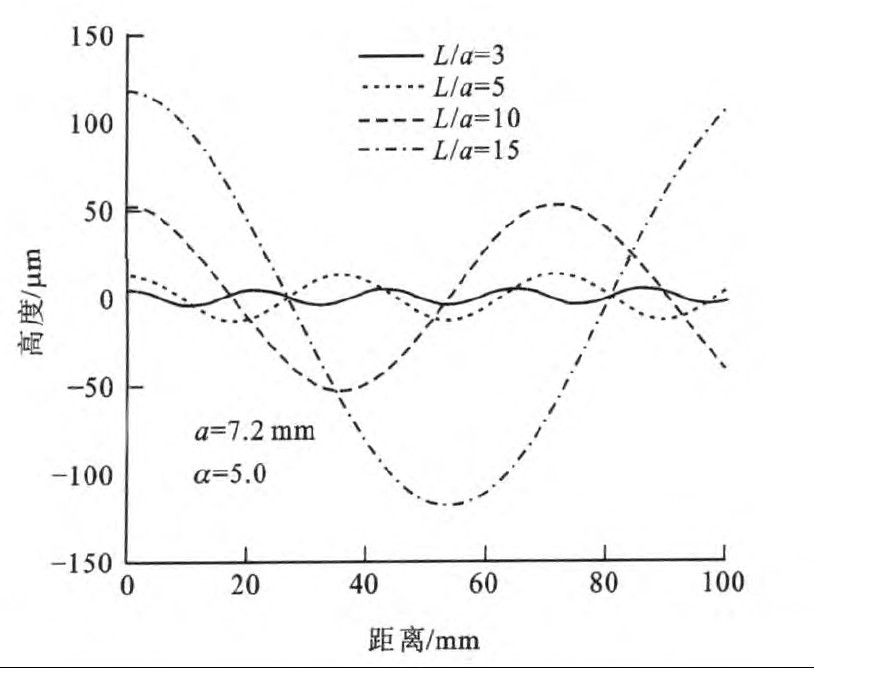
α越大, 表示钢轨波磨的程度越浅, α越小, 表示钢轨波磨程度越深, 图 2给出了相同波长不同深度的波磨比较。对于不同的波长和幅值的波磨, 如果其α相同, 则认为它们具有相同的深度, 图 3给出了几组等深度波磨的幅值和波长, 图 4给出了一组等深度的波磨波形, 可见随着波长的增大, 幅值呈二次方增长。引入波磨深度指数的概念, 一方面为了衡量波磨的发展程度, 另一方面是为了对波磨进行分组, 用于求解传递函数。
图 2 同波长不同深度的波磨Figure 2. Corrugation waveforms with equal wavelength and different shallowness factors
图 3 等深度波磨的幅值和波长关系Figure 3. Relationship between amplitudes and wavelengths of corrugations with equal shallowness factor2. 三维滚动接触的数值算法
Kalker运用变分法, 将滚动接触问题的最小余能原理表达为一个数学优化问题[13]。本文使用MATLAB程序实现了Kalker的三维滚动接触算法。首先设置潜在的接触区为矩形以便于编程, 并划分为N个单元, 每个单元可能属于粘着区、滑动区与非接触区, 每个单元内的法向应力和切向应力为定值。然后使用Newton-Raphson算法先优化求解法向接触方程组, 将其结果代入切向接触方程组优化求解。当前状态计算完成后, 车轮向前移动一个单元长度, 根据前一时刻的状态重新优化求解该时刻的余能方程。法向接触的优化问题为
式中: F1为法向接触优化目标函数; pi为接触单元的法向应力(未知); i、j为潜在接触区的单元坐标; N为单元数; hi为接触单元的非变形位移; Aij为各单元之间的法向应力和位移之间的影响系数; Δx、Δy为单元的长度; P0为法向正压力。
切向接触的优化问题为
式中: F2为切向接触优化目标函数; qiβ为接触单元的切向应力(未知); β、γ为1表示切向方向x, β、γ为2表示切向方向y; Aiβjγ表示切向应力和位移之间的影响系数; Wiβ为i单元从前时刻t′到当前时刻t总的刚体滑动量; u′iβ为i单元从前时刻到t′时刻的弹性位移差; qi是单元的切向合力; μ为摩擦因数, 取0.4。
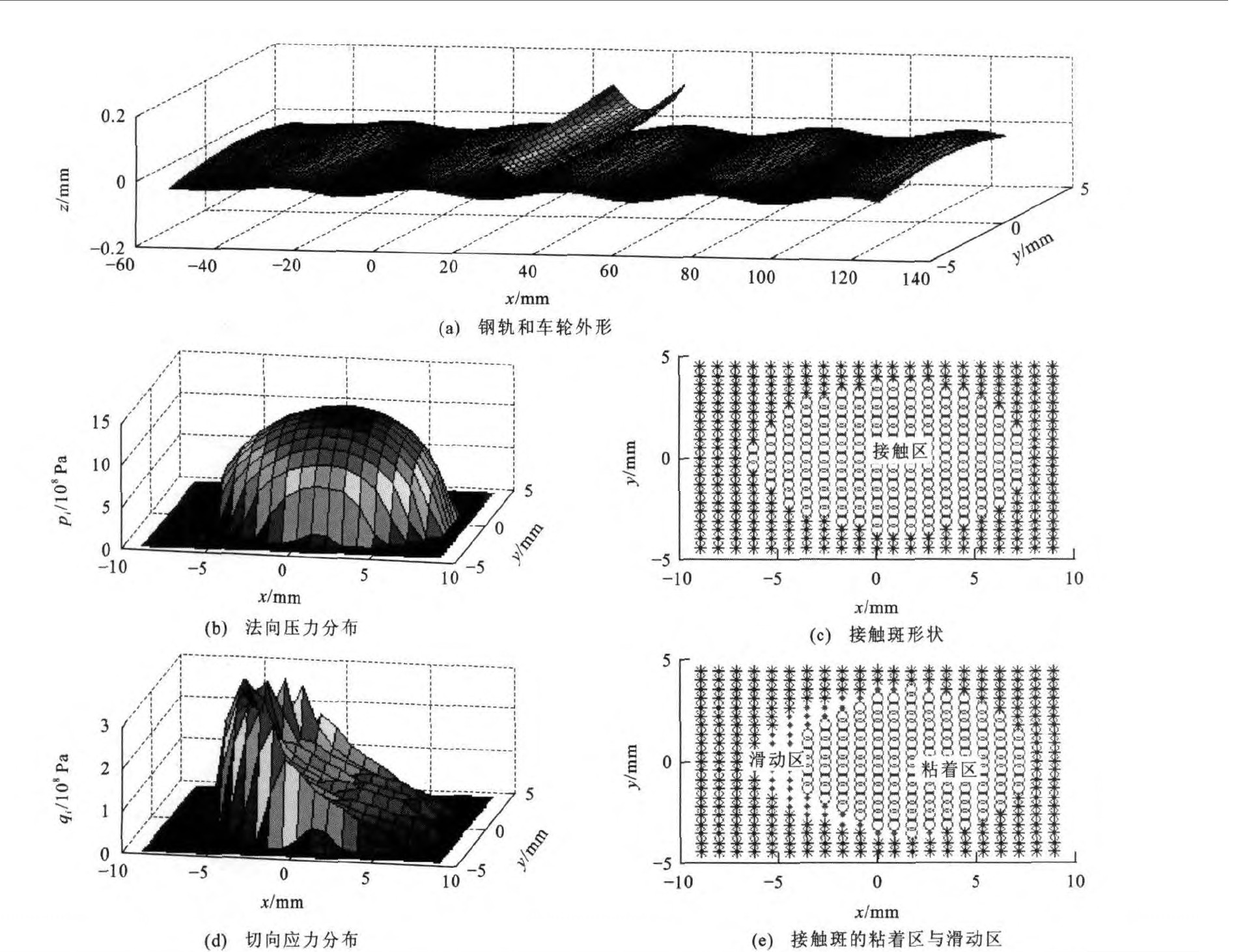
图 5给出了车轮在具有简谐波磨的钢轨上滚动时的接触斑和应力分布, 其中x为钢轨纵向长度, y为钢轨横向长度, z为波磨的高度。可见, 当钢轨上存在短波波磨时, 轮轨之间的滚动接触斑不再是椭圆形, 并且接触斑沿前进方向出现“移动”现象, 法向应力沿前进方向也不对称。
3. 短波波磨状态的纵向蠕滑力特性
在小蠕滑状态下, 假设短波波磨具有简谐波形, 采用Kalker三维滚动接触的MATLAB程序计算非稳态的蠕滑力, 并与由沈氏理论计算的稳态蠕滑力进行对比[14]。
3.1 计算参数
计算的参数如下: 车轮半径Rw为500 mm; 法向力P0为70 kN。车轮和钢轨的主轮廓线半径见表 1, 接触斑长(2a)短(2b)轴比a/b为2.0代表新轮新轨状态, a/b为0.5代表磨耗后的轮轨状态。接触斑半径a、b是静态值。纵向蠕滑率取0.1%与0.2%两种水平。
表 1 轮轨参数Table 1. Wheel and rail parameters
3.2 纵向蠕滑力特性
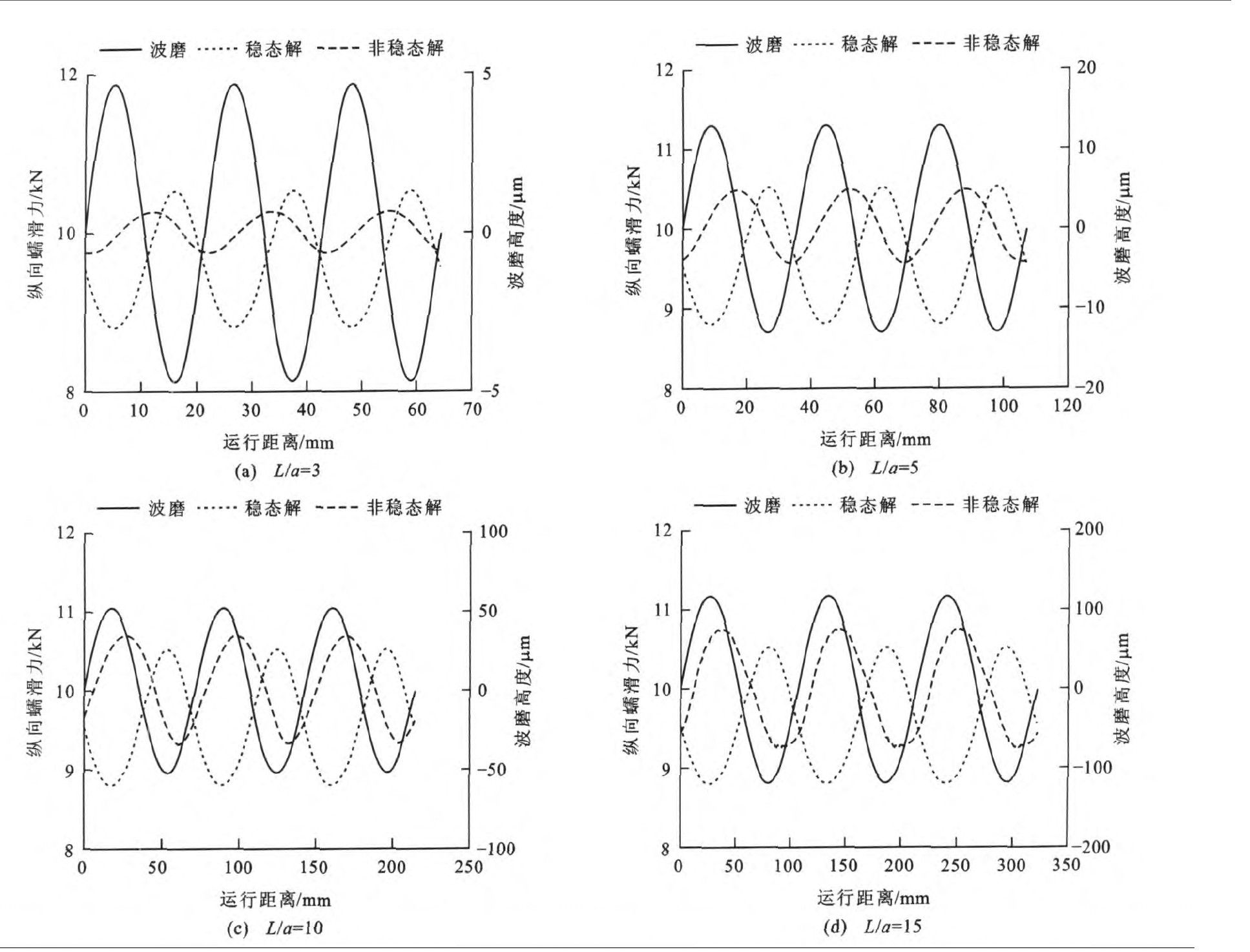
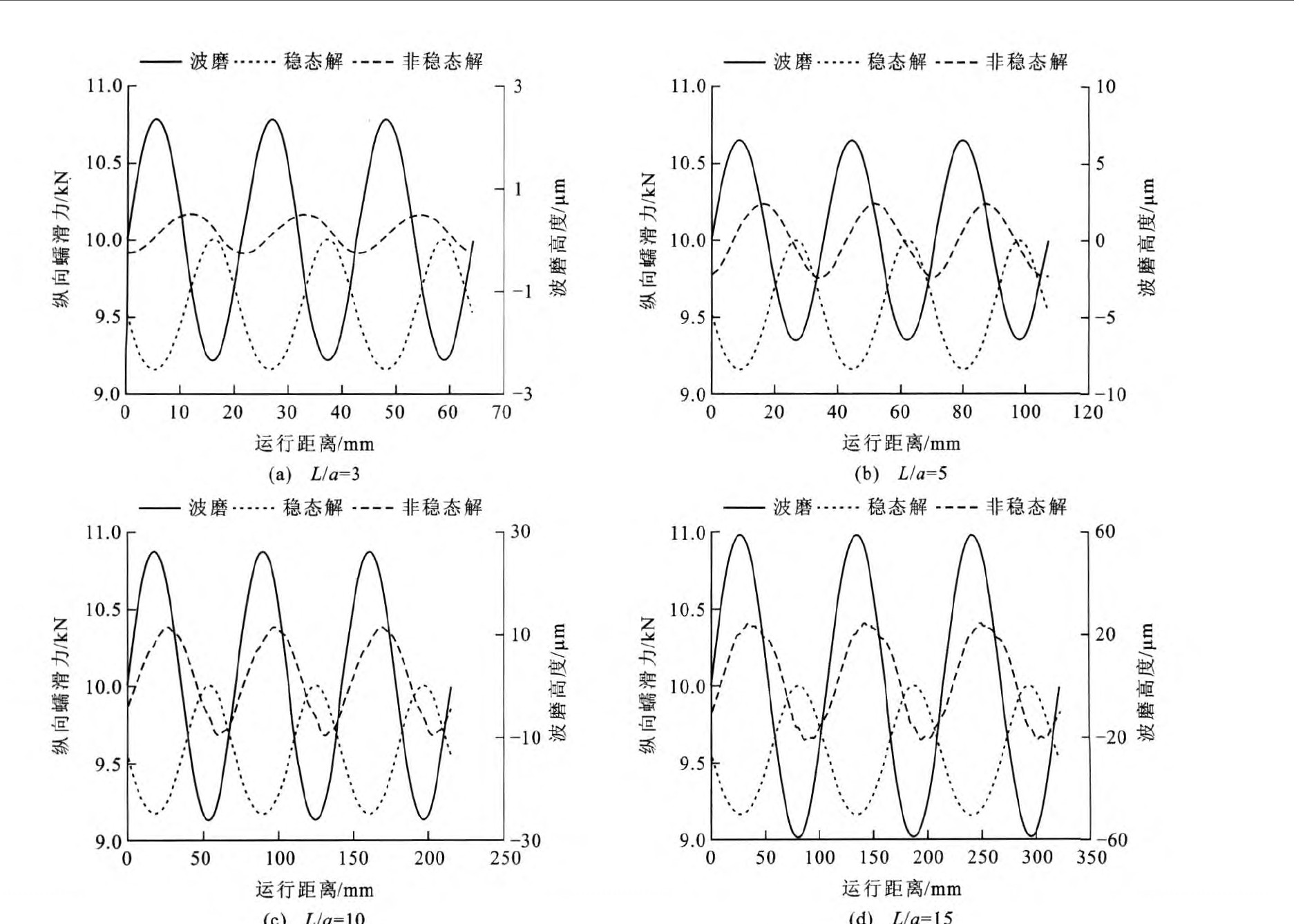
图 6给出了纵向蠕滑率取0.1%, α为5.0, a/b为2.0时, 由非稳态和稳态理论求得的纵向蠕滑力。可见, 纵向蠕滑力由两部分组成: 直流分量和波动分量, 其中波动分量是引起钢轨短波波磨的主要原因(直流分量导致的磨耗是均匀的)。由稳态理论计算出的纵向蠕滑力总是在波磨的波峰处最小, 波谷处最大, 其波形的相位正好与波磨的波形相位相反, 而与L/a无关。在同等深度波磨的情况下, 由稳态理论计算出的纵向蠕滑力是相同的。而由非稳态理论计算出的纵向蠕滑力明显与L/a有关: L/a越小, 波动分量的幅值越小, 相位越滞后于波磨的波形; L/a越大, 波动分量的幅值越大, 相位滞后于波磨的波形越不明显。
图 6 α为5.0时的短波波磨的纵向蠕滑力Figure 6. Longitudinal creep forces under short-pitch corrugations when α is 5.0图 7给出了纵向蠕滑率取0.1%, α为10.0, a/b为2.0时, 由非稳态和稳态理论求得的纵向蠕滑力。可见, 具有与图 6类似的规律。对比图 6看出, 波磨越浅, 纵向蠕滑力的波动分量越小; 波磨越深, 纵向蠕滑力的波动分量越大。
图 7 α为10.0时短波波磨的纵向蠕滑力Figure 7. Longitudinal creep forces under short-pitch corrugations when α is 10.0上述分析表明, 钢轨存在短波波磨时, 由非稳态理论求得的纵向蠕滑力明显不同于稳态理论的计算结果。如果按照稳态理论计算出的蠕滑力的变化趋势来分析磨耗结果, 就会得出在波峰处磨耗少, 波谷处磨耗多的结论, 这与由非稳态理论得到的结论相悖。如果使用稳态蠕滑理论分析短波波磨的成因, 可能会得到错误的结论。
3.3 传递函数
定义非稳态蠕滑力中波动分量的增益g为
式中: Fn为非稳态纵向蠕滑力波动分量ΔFn的幅值; Fs为稳态纵向蠕滑力波动分量ΔFs的幅值。
非稳态蠕滑力波动分量与波磨波形的相位差φ为
式中: φ1为纵向蠕滑力波动分量的相位角。
图 8给出了根据式(5)、(6)得到的等深度情况下, 纵向蠕滑力的波动分量随波长比L/a变化的Nyquist图, 图中的点表示计算值, 曲线表示拟合的传递函数。可见, 随着L/a减小, 纵向蠕滑力波动的幅值逐渐减小, 滞后相位逐渐增大。一个值得注意的现象是相同的波长比L/a时, 不同深度短波波磨的纵向蠕滑力增益基本相同, 相位差也接近。接触斑长短轴比a/b越大, 则波动分量的幅值越大; a/b越小, 则波动分量的幅值越小。
图 8 纵向蠕滑力的Nyquist图和传递函数Figure 8. Nyquist figures and transfer functions of longitudinal creep forces对图 8的Nyquist图, 采用频率响应的系统辨识方法[15]可以拟和得到以下的二阶传递函数
式中: c0、c1、c2为拟合常数, 见表 2。
表 2 传递函数H的系数Table 2. Parameters of transfer function H
式(7)表明在等深度条件下, 非稳态纵向蠕滑力的波动分量具有大阻尼二阶系统的传递特性。值得注意的是, 在相同蠕滑率与相同接触斑长短轴比a/b的情况下, 各深度的传递函数系数相差不大。
这说明当蠕滑率和a/b确定后, 式(7)中的拟合常数c0、c1、c2可以取一个定值。
3.4 传递函数的应用
3.4.1 等深度多频段短波波磨
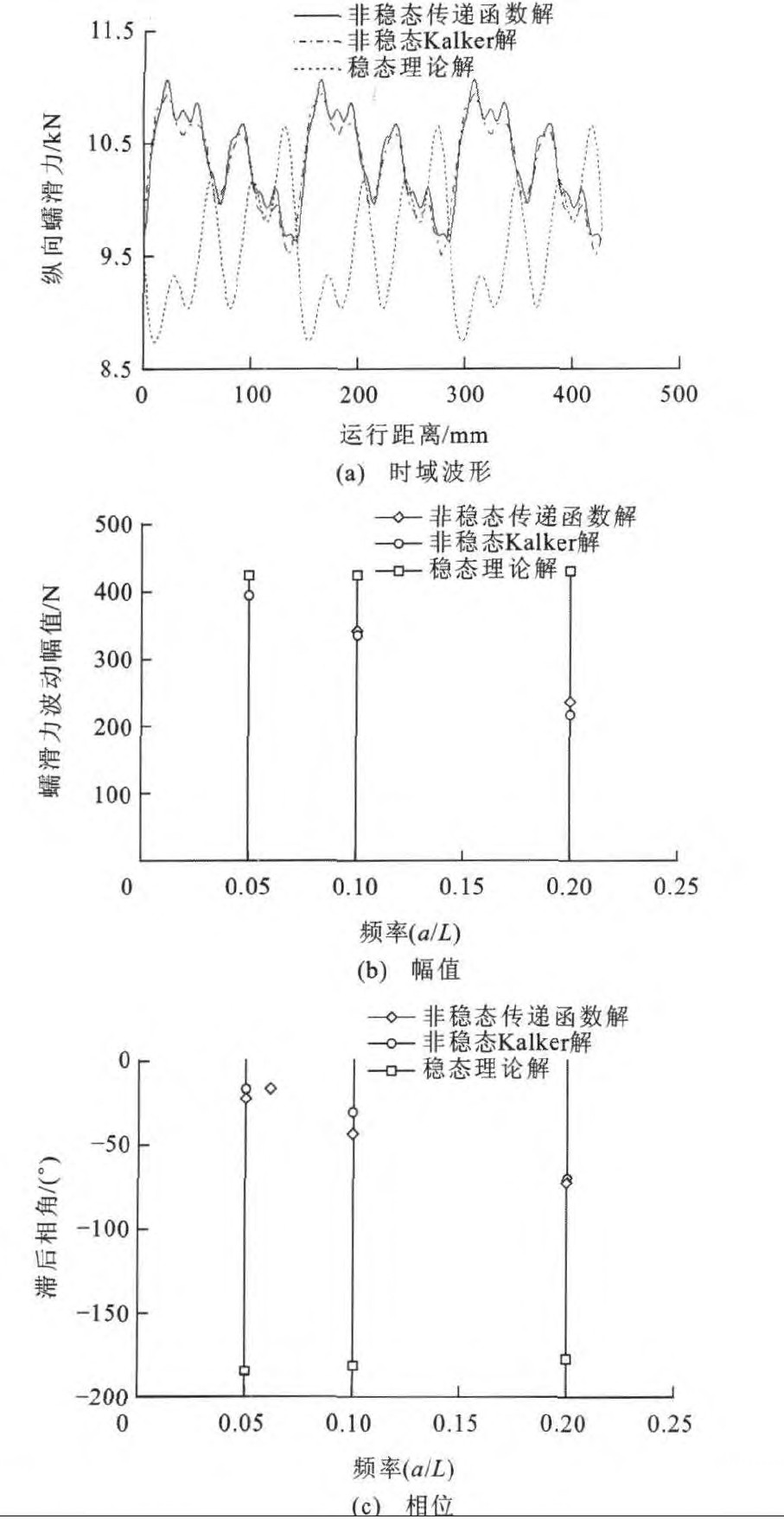
假设短波波磨深度指数α为5.0, 由波长比L/a为5、10、20的3个频段组成, a/b取2.0, 纵向蠕滑率取0.1%。图 9(a)给出了由传递函数式(7)和Kalker数值理论计算得到的纵向蠕滑力, 两者的波形几乎一样。同样的结论也反映在频域上, 见图 9(b)、(c), 这说明传递函数可以适用于等深度多频段波磨的纵向蠕滑力计算。图 9同时给出了由稳态理论计算得到的波形, 由稳态理论得到的纵向蠕滑力明显不同于Kalker的数值解, 在频域上总是滞后180°, 并且高估了纵向蠕滑力高频段的波动分量。
图 9 等深度多频段波磨的纵向蠕滑力Figure 9. Longitudinal creep forces of multi-frequency corrugations with equal shallowness factor3.4.2 不等深度多频段短波波磨
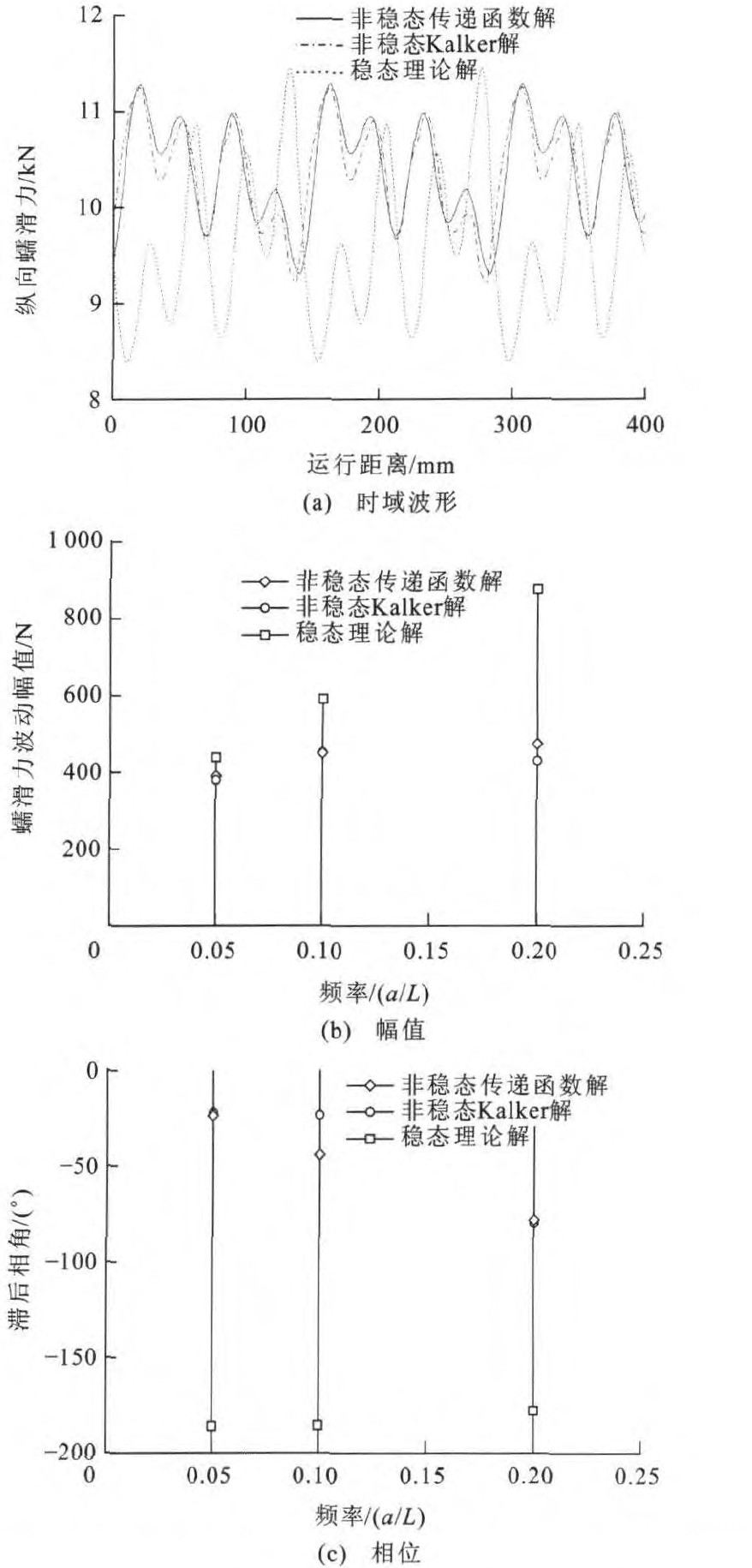
假设短波波磨由以下3个频率成分组成: 深度指数α为5.0, 波长比L/a为5;深度指数α为7.5, 波长比L/a为10;深度指数α为10.0, 波长比L/a为20。a/b为2.0, 纵向蠕滑率为0.1%。
图 10(a)给出了由传递函数式(7) 和Kalker的数值理论计算得到的纵向蠕滑力, 两者的波形非常接近, 同样的结论也反映在频域上, 见图 9(b)、(c), 这说明传递函数也可以适用于不等深度多频段波磨的纵向蠕滑力计算。图 10同时给出了由稳态理论计算得到的波形, 由稳态理论得到的纵向蠕滑力明显不同于Kalker的数值解, 在频域上总是滞后180°, 也高估了纵向蠕滑力高频段的波动分量。
图 10 不等深度多频段波磨的纵向蠕滑力Figure 10. Longitudinal creep forces of multi-frequency corrugations with different shallowness factors综合上述分析可以推论, 传递函数式(7)能够适用于宽频各深度短波波磨的纵向蠕滑力计算。
4. 结语
由于短波波磨的波长L与接触斑半径a在同一数量级范围内, 由Kalker三维滚动接触理论得到的纵向蠕滑力与由稳态滚动理论计算出的纵向蠕滑力存在明显差别。在小蠕滑条件下, 短波波磨纵向蠕滑力波动分量随着波长比L/a的变化产生明显的幅值衰减和相位滞后, 当短波波磨按照简谐规律波动时, 其纵向蠕滑力波动分量与稳态理论的计算值之间可用波长比L/a的传递函数来描述。相同的蠕滑率和接触斑半径时, 不同深度短波波磨的纵向蠕滑力波动分量的传递函数近似一致, 利用传递函数可以快速计算短波波磨纵向蠕滑力。
目前, 求解非稳态滚动接触问题主要依靠Kalker三维滚动接触精确理论及其相应的数值算法, 非稳态滚动接触蠕滑力的快速算法仍然是一个待解决的问题。本文的研究发现, 短波波磨简谐波动时, 等深度的纵向蠕滑力也可以用波长比L/a的传递函数来表达。那么, 正压力简谐波动时的蠕滑力是否也具有类似的特性和传递函数呢?当蠕滑率、正压力和接触几何同时按简谐规律变化时, 非稳态蠕滑力是否还具有类似的传递函数?这些问题仍有待于研究。
-
图 2 同波长不同深度的波磨
Figure 2. Corrugation waveforms with equal wavelength and different shallowness factors
图 3 等深度波磨的幅值和波长关系
Figure 3. Relationship between amplitudes and wavelengths of corrugations with equal shallowness factor
图 6 α为5.0时的短波波磨的纵向蠕滑力
Figure 6. Longitudinal creep forces under short-pitch corrugations when α is 5.0
图 7 α为10.0时短波波磨的纵向蠕滑力
Figure 7. Longitudinal creep forces under short-pitch corrugations when α is 10.0
图 8 纵向蠕滑力的Nyquist图和传递函数
Figure 8. Nyquist figures and transfer functions of longitudinal creep forces
图 9 等深度多频段波磨的纵向蠕滑力
Figure 9. Longitudinal creep forces of multi-frequency corrugations with equal shallowness factor
图 10 不等深度多频段波磨的纵向蠕滑力
Figure 10. Longitudinal creep forces of multi-frequency corrugations with different shallowness factors
-
[1] GRASSIE S L, KALOUSEKJ. Rail corrugation: characteristics, causes and treat ments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1993, 207(1): 57-68. doi: 10.1243/PIME_PROC_1993_207_227_02 [2] 温泽峰. 钢轨波浪形磨损研究[D]. 成都: 西南交通大学, 2006.WEN Ze-feng. Study on rail corrugation[D]. Chengdu: Southwest Jiaotong University, 2006. (in Chinese) [3] MÜLLER S. Alinear wheel-track model to predict instability and short pitch corrugation[J]. Journal of Sound and Vibration, 1999, 227(5): 899-913. doi: 10.1006/jsvi.1999.2981 [4] HEMPELMANN K, KNOTHE K. An extended linear model for the prediction of short pitch corrugation[J]. Wear, 1996, 191(1/2): 161-169. [5] XIE GANG, IWNICKI S D. Calculation of wear on a corrugated rail using a three-dimensional contact model[J]. Wear, 2008, 265(9/10): 1238-1246. [6] XIE GANG, IWNICKI S D. Simulations of roughness growth on rails-results from non-Hertzain, non-steady contact model[J]. Vehicle System Dynamics, 2008, 46(1/2): 117-128. [7] KNOTHE K, GROSS-THEBING A. Short wavelength rai lcorrugation and non-steady-state contact mechanics[J]. Vehicle System Dynamics, 2008, 46(1/2): 49-66. [8] KALKER J J. Transient phenomena in two elastic cylindersrolling over each other with dry friction[J]. Journal of Applied Mechanics, 1970, 37(3): 677-688. doi: 10.1115/1.3408597 [9] KNOTHE K, GROSS-THEBING A. Derivation of frequency dependent creep coefficients based on an elastic half-space model[J]. Vehicle System Dynamics, 1986, 15(3): 133-153. doi: 10.1080/00423118608968848 [10] GROSS-T HEBING A. Frequency-dependent creep coefficients for three-dimensional rolling contact problem[J]. Vehicle System Dynamics, 1989, 18(6): 359-374. doi: 10.1080/00423118908968927 [11] ALONSO A, GIM? NEZ J. Non-steady state modelling of wheel-rail contact problem for the dynamic simulation of railway vehicles[J]. Vehicle System Dynamics, 2008, 46(3): 179-196. doi: 10.1080/00423110701248011 [12] PIOTROWSKI J, KALKER J J. A non-linear mathematical model for finite, periodic rail corrugations[C]∥ALIABALI M H, BREBBIA C A. The First International Conference on Contact Mechanics. Southampton: Computational Mechanics Inc., 1993: 413-424. [13] KALKER J J. Three-Dimension Elastic Bodies in Rolling contact[M]. Dordrecht: Kluwer Academic Publishers, 1990. [14] SHEN Z Y, HEDRICK J K, ELKINS J. A comparison of alternative creep force models for rail vehicle dynamic analysis[J]. Vehicle System Dynamics, 1983, 12(1): 70-82. [15] 潘立登, 潘仰东. 系统辨识与建模[M]. 北京: 化学工业出版社, 2004.PAN Li-deng, PAN Yang-dong. System Identification and Modelling[M]. Beijing: Chemical Industry Press, 2004. (in Chinese) -
下载:
下载:
点击查看大图
计量
- 文章访问数: 1006
- HTML全文浏览量: 184
- PDF下载量: 617
- 被引次数: 0
