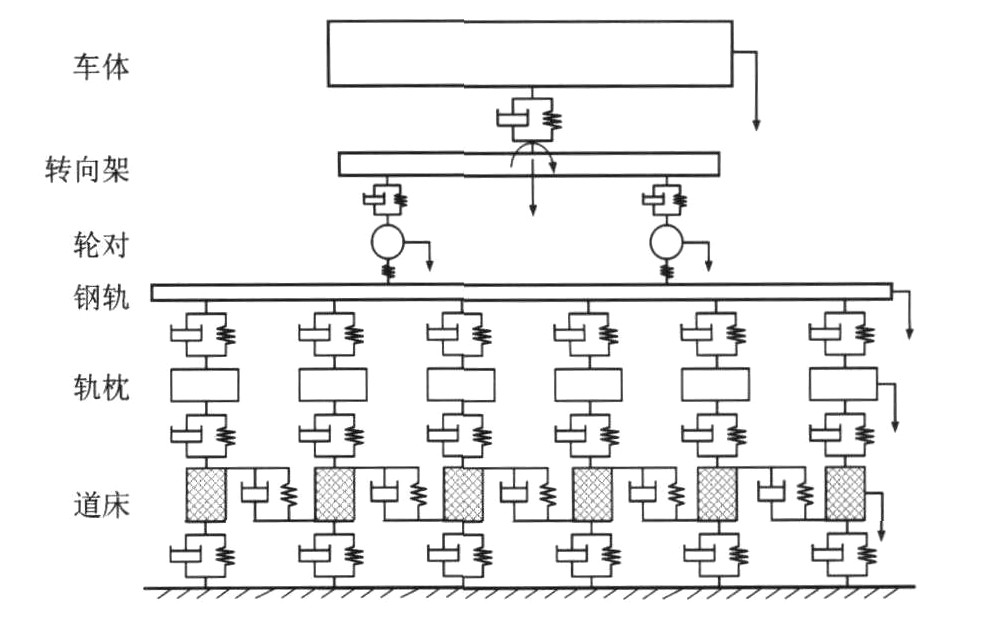
Solution methods of rail model in vehicle-track coupling dynamics
-
摘要: 应用车辆-轨道非线性耦合动力学模型, 分析了采用解析方法的模态叠加法、有限元法的模态叠加法和有限元法的直接积分法求解车辆-轨道耦合动力学钢轨模型的计算精度与计算效率。选取Bernoulli-Euler梁或Rayleigh-Timoshenko梁模拟钢轨, 采用不同类型单元离散钢轨模型, 并利用显式积分方法求解车辆-轨道耦合动力学的响应。计算结果表明: 当采用Bernoulli-Euler梁钢轨模型和轨道激励频率较低时, 采用协调质量阵的直接积分法计算时间是解析方法的模态叠加法的28.8倍, 各种计算方法的计算结果接近; 当采用Rayleigh-Timoshenko梁钢轨模型和轨道激励频率较低时, 可以忽略Rayleigh-Timoshenko梁的转动惯量对车辆-轨道耦合动力学模型的响应影响; 解析法的模态叠加法的计算时间比混合单元的慢64.5%。
-
关键词:
- 钢轨模型 /
- 有限元法 /
- 模态叠加法 /
- Bernoulli-Euler梁 /
- Rayleigh-Timoshenko梁
Abstract: The computational accuracies and efficiencies of different methods for solving dynamic rail model were investigated with vehicle-track nonlinear coupling dynamics model. The methods were modal superposition method based on analytical expression, modal superposition method based on FEM, and direct integration method based on FEM. Rail was modeled by Bernoulli-Euler beam or Rayleigh-Timoshenko beam, and rail model was divided by different types of elements. The response of vehicle-track coupling dynamics was solved with explicit integration method. Calculation result indicates that the computational time of direct integration method based on consistent mass matrix is 28.8 times than that of modal superposition based on analytical expression when rail is modeled by Bernoulli-Euler beam and track excitation frequency is lower, and the computational accuracies of the methods are nearly same. The response influence of rotatory inertia for Rayleigh-Timoshenko beam in vehicle-track coupling dynamics model can be neglected when rail is modeled by Rayleigh-Timoshenko beam and track excitation frequency is lower. The computational time of modal superposition method based on analytical expression is 64.5% slower than that of hybrid element. -
表 1 不同计算方法的计算时间1
Table 1. Computational times 1 of different methods
计算方法 积分步长/μs 计算时间/s 解析方法的模态叠加法 42.1 1.427 有限元法的协调质量阵 2.6 41.099 有限元法的集中质量阵1 11.2 2.359 有限元法的集中质量阵2 6.2 4.172 有限元法的模态叠加法 41.8 7.266 表 2 不同计算方法的计算时间2
Table 2. Computational times 2 of different methods
计算方法 积分步长/μs 计算时间/s 解析方法的模态叠加法 13.4 4.370 有限元法的协调质量阵 2.6 41.099 有限元法的集中质量阵1 11.2 2.359 有限元法的集中质量阵2 6.2 4.172 有限元法的模态叠加法 14.3 17.896 表 3 不同计算方法的计算时间3
Table 3. Computational times 3 of different methods
计算方法 积分步长/μs 计算时间/s 解析方法的模态叠加法 28.2 2.089 有限元法的D单元 6.0 45.699 有限元法的T单元 19.6 5.620 有限元法的EMTK单元 10.7 2.458 表 4 不同计算方法的计算时间4
Table 4. Computational times 4 of different methods
计算方法 积分步长/μs 计算时间/s 解析方法的模态叠加法 14.3 4.266 有限元法的D单元 6.0 45.699 有限元法的T单元 14.3 7.489 有限元法的EMTK单元 10.3 2.594 -
[1] 刘建新, 易明辉, 王开云. 重载铁路车轮踏面擦伤时的轮轨动态相互作用特征[J]. 交通运输工程学报, 2010, 10 (3): 52-56. doi: 10.3969/j.issn.1671-1637.2010.03.009LIU Jian-xin, YI Ming-hui, WANG Kai-yun. Characteristic of dynamic interaction between wheel and rail due to wheel tread flat on heavy haul railway[J]. Journal of Traffic and Transportation Engineering, 2010, 10 (3): 52-56. (in Chinese) doi: 10.3969/j.issn.1671-1637.2010.03.009 [2] YOUNG T H, LI C Y. Vertical vibration analysis of vehicle/imperfect track systems[J]. Vehicle System Dynamics, 2003, 40 (5): 329-349. doi: 10.1076/vesd.40.5.329.17912 [3] KASSA E, NIELSEN J C O. Dynamic train-turnout interactionin an extended frequency range using a detailed model of track dynamics[J]. Journal of Sound and Vibration, 2009, 320 (4/5): 893-914. [4] DUKKIPATI R V, DONG R G. The dynamic effects of conventional freight car running over a dipped-joint[J]. Vehicle System Dynamics, 1999, 31 (2): 95-111. doi: 10.1076/vesd.31.2.95.2095 [5] 任尊松. 车辆-道岔系统动力学研究[D]. 成都: 西南交通大学, 2000.REN Zun-song. Research on the vehicle-turnout system dynamics[D]. Chengdu: Southwest Jiaotong University, 2000. (in Chinese) [6] NEWTON S G, CLARK R A. An investigation into the dynamic effects onthetrack of wheelflats onrailway vehicles[J]. Journal of Mechanical Engineering Science, 1979, 21 (4): 287-297. doi: 10.1243/JMES_JOUR_1979_021_046_02 [7] DONG R G, SANKAR S, DUKKIPATI R V. Afinite element model of railway track andits applicationto the wheel flat problem[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1994, 208 (1): 61-72. doi: 10.1243/PIME_PROC_1994_208_234_02 [8] 徐志胜, 翟婉明, 王开云. 基于Timoshenko梁模型的车辆-轨道耦合振动分析[J]. 西南交通大学学报, 2003, 38 (1): 22-27. doi: 10.3969/j.issn.0258-2724.2003.01.006XU Zhi-sheng, ZHAI Wan-ming, WANG Kai-yun. Analysis of vehicle-track coupling vibration based on Timoshenko beam model[J]. Journal of Southwest Jiaotong University, 2003, 38 (1): 22-27. (in Chinese) doi: 10.3969/j.issn.0258-2724.2003.01.006 [9] 徐志胜, 翟婉明, 王开云, 等. 车辆-轨道系统振动响应分析——Timoshenko梁与Euler梁轨道模型的比较[J]. 地震工程与工程振动, 2003, 23 (6): 74-79. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200306012.htmXU Zhi-sheng, ZHAI Wan-ming, WANG Kai-yun, et al. Analysis of vehicle-track system vibration—comparison between Timoshenko beam and Euler beamtrack model[J]. Earthquake Engineering and Engineering Vibration, 2003, 23 (6): 74-79. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200306012.htm [10] KNOTHE K L, GRASSIE S L. Modelling of railway track and vehicle/trackinteraction at high frequencies[J]. Vehicle System Dynamics, 1993, 22 (3/4): 209-262. [11] ZHAI Wan-ming, WANG Kai-yun, CAI Cheng-biao. Fundamentals of vehicle-track coupled dynamics[J]. Vehicle SystemDynamics, 2009, 47 (11): 1349-1376. [12] 徐志胜. 轨道交通轮轨噪声预测与控制的研究[D]. 成都: 西南交通大学, 2004.XU Zhi-sheng. Prediction and control of wheel/rail noise for rail transit[D]. Chengdu: Southwest Jiaotong University, 2004. (in Chinese) [13] HINTON E, ROCK T, ZIENKIEWICZ O C. Anote on mass lumping and related processes in the finite element method[J]. Earthquake Engineering and Structural Dynamics, 1976, 4 (3): 245-249. doi: 10.1002/eqe.4290040305 [14] ZHANG Shu-guang, XIAO Xin-biao, WEN Ze-feng, et al. Effect of unsupported sleepers on wheel/rail normal load[J]. Soil Dynamics and Earthquake Engineering, 2008, 28 (8): 662-673. [15] JIN Xue-song, WENZe-feng, WANG Kai-yun, et al. Three-dimensional train-track model for study of rail corrugation[J]. Journal of Sound and Vibration, 2006, 293 (3/4/5): 830-855. [16] NIELSENJ C O, IGELAND A. Vertical dynamic interaction between train and track-influence of wheel and track imperfections[J]. Journal of Sound and Vibration, 1995, 187 (5): 825-839. -





 下载:
下载: