物流园区服务范围确定方法

孙宝凤; 罗清玉; 许鹏; 郑杨

doi:10.19818/j.cnki.1671-1637.2011.06.013

物流园区服务范围确定方法

doi: 10.19818/j.cnki.1671-1637.2011.06.013

1.
吉林大学交通学院，吉林长春 130025
2.
吉林大学商学院，吉林长春 130012

基金项目:

国家自然科学基金项目 50978115

吉林省科技发展计划项目 20080526

中央高校基本科研业务费专项资金项目 2009JC046

详细信息

作者简介:
孙宝凤(1970-), 女, 吉林大安人, 吉林大学教授, 工学博士, 从事物流系统仿真与供应链管理研究

中图分类号: U491.12
计量
- 文章访问数: 534
- HTML全文浏览量: 91
- PDF下载量: 562
- 被引次数: 0
出版历程
- 收稿日期: 2011-07-24
- 刊出日期: 2011-12-25

Determining method of service scope for logistics park

1.
School of Traffic, Jilin University, Changchun 130025, Jilin, China
2.
School of Business, Jilin University, Changchun 130012, Jilin, China

More Information

Author Bio:
SUN Bao-feng (1970-), female, professor, PhD, +86-431-85094779, sunbf@jlu.edu.cn

摘要

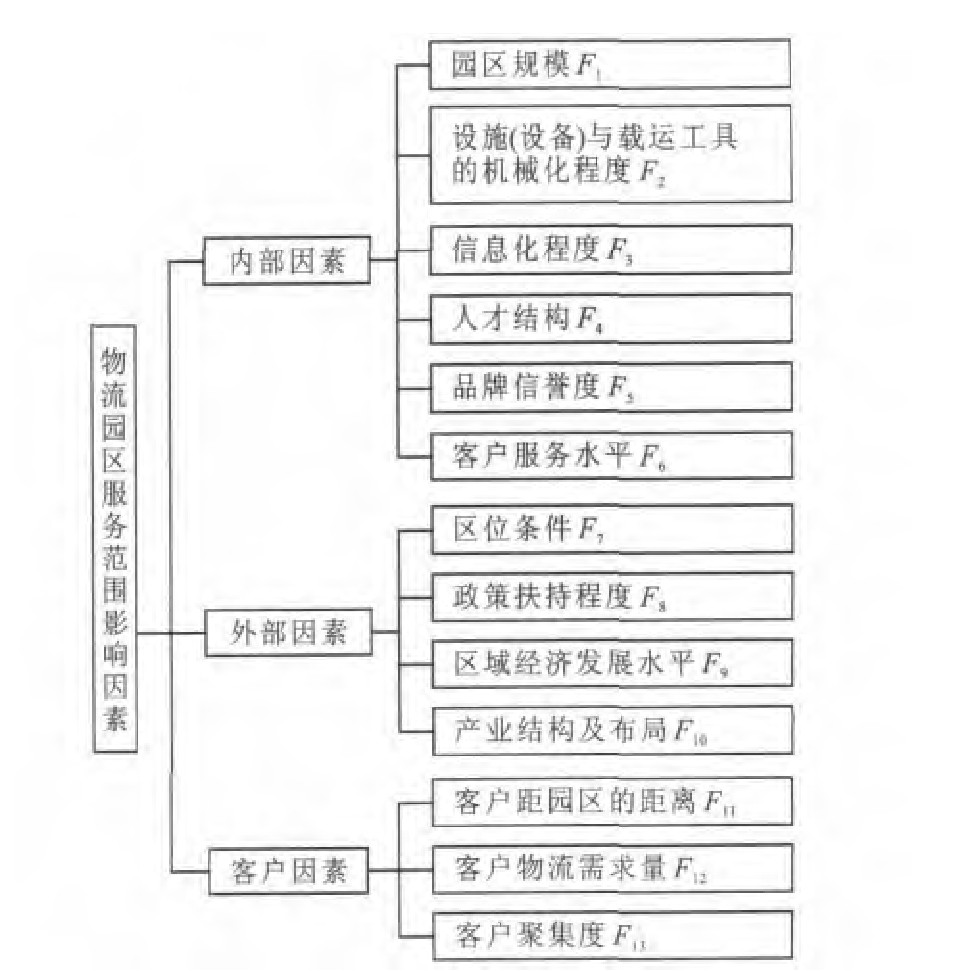
摘要: 考虑了多个物流园区的竞争关系以及客户对物流园区的选择需求, 分析了现有方法解决物流园区服务范围问题的不足, 提出了融合断裂点模型和哈夫概率模型的物流园区服务范围的分步确定方法。以DEMATEL方法为基础, 运用改进的断裂点模型, 分析和遴选出对物流园区服务范围影响程度大的关键因素, 并获得初始空间服务范围。运用改进后的哈夫概率模型, 确定了合理阈值, 并修正了初始空间服务范围。分析结果表明: 对物流园区服务范围影响程度较大的因素分别为政府对物流业的扶持程度、客户物流需求量、区域经济发展水平、物流园区规模、客户服务水平; 运用该方法, 物流园区的单位面积营业额和物流强度分别为10.25×10⁴元·km^-2和8.39×10⁴ t·km·km^-2, 均大于传统方法的指标值10.18×10⁴元·km^-2和8.28×10⁴ t·km·km^-2。可见, 本文提出的方法有效。
- 物流园区 /
- 服务范围 /
- 断裂点模型 /
- 哈夫概率模型 /
- DEMATEL方法 /
- 回归分析
Abstract: Competition relationships among several logistics parks and the selection demand of customer on a certain logistics park were considered.The lack of present method solving the service scope problem of logistics park was analyzed.The step-divided determining method fused with breaking point model and Huff probability model was presented for service scope of logistics park.On the basis of DEMATEL method, the improved breaking point model was utilized to analyze and choose the key factors with high influence on the service scope of logistics park, and initial space service scope was obtained.By using the improved Huff probability model, rational threshold values were identified, and initial space service scope was modified.Analysis result shows that the key factors with high influence on the service scope of logistics park are government supporting to logistics industry, logistics demand of customer, development level of region economy, scale of logistics park and service level of customer respectively.By using the method, the per unit area turnover and logistics strength of logistics park are 10.25×10⁴ yuan·km^-2 and 8.39×10⁴ t·km·km^-2 respectively, while the values are 10.18×10⁴ yuan·km^-2 and 8.28×10⁴ t·km·km^-2 by using traditional method.So the determining method is effective.
- logistics park /
- service scope /
- breaking point model /
- Huff probability model /
- DEMATEL method /
- regression analysis

HTML全文

图 1 影响因素

Figure 1. Influence factors

下载: 全尺寸图片幻灯片

图 2 物流园区服务范围

Figure 2. Service scopes of logistics park

下载: 全尺寸图片幻灯片

表 1 影响因素关系

Table 1. Relationships among influence factors

下载: 导出CSV

表 2 综合数据

Table 2. Comprehensive data

下载: 导出CSV

表 3 中心度

Table 3. Central degrees

下载: 导出CSV

表 4 实际值和计算值

Table 4. Actual values and calculation values

下载: 导出CSV

表 5 不同方法下的评价指标比较

Table 5. Comparison of evaluation indexes under different determining methods

下载: 导出CSV

参考文献(12)

[1]	PAPAZOGLOU C. Greece's potential trade flows: agravity model approach[J]. International Advances in Economic Research, 2007, 13(4): 403-414. doi: 10.1007/s11294-007-9107-x
[2]	姚丽亚, 关宏志. 轨道交通线网服务范围研究[J]. 北京工业大学学报, 2008, 34(7): 738-742. https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD200807014.htm YAO Li-ya, GUAN Hong-zhi. The service regions of rail transit net[J]. Journal of Beijing University of Technology, 2008, 34(7): 738-742. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD200807014.htm
[3]	邵岩, 谢如鹤. 基于引力模型的物流园区空间服务范围[J]. 物流技术, 2006, 25(7): 131-133. doi: 10.3969/j.issn.1005-152X.2006.07.042 SHAO Yan, XIE Ru-he. Service area of logistics park based on gravity model[J]. Logistics Technology, 2006, 25(7): 131-133. (in Chinese) doi: 10.3969/j.issn.1005-152X.2006.07.042
[4]	邱慧芳, 郝生跃. 基于引力模型的配送中心服务范围研究[J]. 物流技术, 2010, 29(2): 82-84. https://www.cnki.com.cn/Article/CJFDTOTAL-WLJS2010Z1027.htm QIU Hui-fang, HAO Sheng-yue. Study on the service scope of distribution centers based on gravity model[J]. Logistics Technology, 2010, 29(2): 82-84. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLJS2010Z1027.htm
[5]	江从发, 龚国华, 丁明芳. 配送中心最佳服务半径分析[J]. 物流技术, 2003, 22(9): 19-23. https://www.cnki.com.cn/Article/CJFDTOTAL-WLJS200309006.htm JIANG Cong-fa, GONG Guo-hua, DING Ming-fang. Analysis on optimized service radium for a distribution center[J]. Logistics Technology, 2003, 22(9): 19-23. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLJS200309006.htm
[6]	范月娇, 张爽. 多源多目标环境下配送中心服务半径的确定(模型研究)[J]. 北京交通大学学报: 社会科学版, 2007, 6(4): 25-29. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJD200704006.htm FAN Yue-jiao, ZHANG Shuang. Determining method of service radius for distribution center in multiple sources and multiple targets environment[J]. Journal of Beijing Jiaotong University: Social Sciences Edition, 2007, 6(4): 25-29. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BFJD200704006.htm
[7]	丁涛, 代舒, 蒋军. 基于引力模型和群决策理论的物流园区空间吸引范围[J]. 水运工程, 2009(12): 24-26. https://www.cnki.com.cn/Article/CJFDTOTAL-SYGC200912013.htm DING Tao, DAI Shu, JIANG Jun. Discussion of spacial attracting scope of logistics park based on gravity model and theory of group decision[J]. Port and Waterway Engineering, 2009(12): 24-26. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SYGC200912013.htm
[8]	APPLEBAUM W. Methods for determining store trade areas, market penetration and potential[J]. Journal of Marketing Research, 1996, 3(2): 127-141.
[9]	BARAV J, CLIQUET G. Delineating store trade areas through morphological analysis[J]. European Journal of Operation Research, 2007, 182(2): 886-898.
[10]	王洁玉. 基于断裂点理论的中心城市空间影响范围变化研究[J]. 河北省科学院学报, 2010, 27(1): 56-59. https://www.cnki.com.cn/Article/CJFDTOTAL-HBKX201001017.htm Wang Jie-yu. Change of the attractived region of central cities based on the breakpoint theory[J]. Journal of the Hebei Academy of Sciences, 2010, 27(1): 56-59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HBKX201001017.htm
[11]	张宇, 吴璟. 基于零售物业竞争关系的商圈测定方法[J]. 商业研究, 2007(8): 194-197. https://www.cnki.com.cn/Article/CJFDTOTAL-BUSI200708056.htm ZHANG Yu, WU Jing. Defining trading area based on competitive relationship[J]. Commercial Research, 2007(8): 194-197. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BUSI200708056.htm
[12]	王发年. 基于满意度原理的物流节点服务半径研究[D]. 西安: 西安电子科技大学, 2010. WANG Fa-nian. Research on service radius of logistics node based on the satisfactory degree theory[D]. Xi'an: Xidian University, 2010. (in Chinese)