中心式诱导路径优化计算方法

龚勃文; 林赐云; 杨兆升; 李静

doi:10.19818/j.cnki.1671-1637.2011.06.017

中心式诱导路径优化计算方法

doi: 10.19818/j.cnki.1671-1637.2011.06.017

龚勃文^{1, 2,},
林赐云^{1, 2},
杨兆升^{1, 2},
李静^{1, 3}

1.
吉林大学汽车仿真与控制国家重点实验室, 吉林长春 130025
2.
吉林大学交通学院, 吉林长春 130025
3.
吉林大学汽车工程学院, 吉林长春 130025

基金项目:

中国博士后基金项目 20100481054

中国博士后基金项目 2011M500615

国家自然科学基金项目 61074137

详细信息

作者简介:
龚勃文(1982-), 女, 黑龙江伊春人, 吉林大学讲师, 工学博士, 博士后, 从事动态交通诱导系统研究

中图分类号: U491.12
计量
- 文章访问数: 690
- HTML全文浏览量: 95
- PDF下载量: 752
- 被引次数: 0
出版历程
- 收稿日期: 2011-07-15
- 刊出日期: 2011-12-25

Calculation method of central guidance path optimization

GONG Bo-wen^{1, 2
,},
LIN Ci-yun^{1, 2},
YANG Zhao-sheng^{1, 2},
LI Jing^{1, 3}

1.
State Key Laboratory of Automobile Simulation and Control, Jilin University, Changchun 130025, Jilin, China
2.
School of Traffic, Jilin University, Changchun 130025, Jilin, China
3.
School of Automotive Engineering, Jilin University, Changchun 130025, Jilin, China

More Information

Author Bio:
GONG Bo-wen(1982-), female, lecturer, PhD, +86-431-85095767, gongbowen1982@gmail.com

摘要

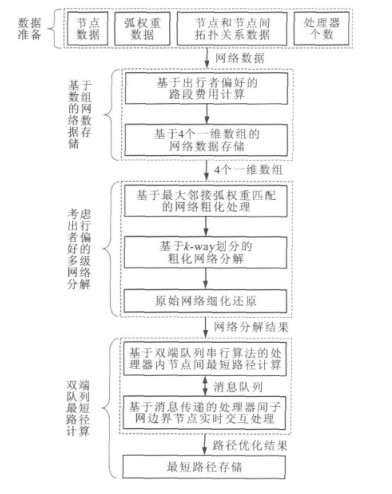
摘要: 基于并行计算技术和网络数据存储方法, 考虑了出行者的偏好, 分析了多级网络分解方法和双端队列最短路径计算方法, 提出了一种新的中心式诱导路径优化计算方法。以长沙市和长春市城市路网的实际数据为基础, 在普通PC机群、联想服务器机群及惠普工作站机群3种不同计算性能的并行计算平台上进行试验测试。测试结果表明: 使用网络数据存储方法, 能够直接确定邻接节点与相应弧的存储位置, 节点信息的查询时间明显减小; 使用多级网络分解方法, 主要路段作为被切割弧的概率降低, 最短路径计算过程中处理器的通信量减小; 使用双端队列最短路径计算方法, 最短路径计算速度明显提升; 使用新的计算方法, 长沙市路网中400万条最短路径计算时间为46s, 长春市路网中1 170万条最短路径计算时间为72s, 完全能够满足中心式诱导路径优化时间小于5min的要求。
- 交通控制 /
- 中心式诱导 /
- 最短路径 /
- 多级网络分解 /
- 双端队列算法 /
- 出行者偏好
Abstract: Based on parallel calculation technology and network data storage method, traveler preferences were considered, the multi-level network decomposing method and the shortest path calculation method of deque were analyzed, and a new central guidance path optimization calculation method was put out. On the basis of the practical data of road networks in Changsha City and Changchun City, and tests on three different parallel calculation platforms including ordinary PC cluster, Lenovo server cluster and HP workstation cluster were carried out. Test result indicates that by using network data storage method, the storage locations of adjacency nodes and corresponding arcs can be determined directly, and the query time of node information obviously decreases. According to multi-level network decomposing method, the probability of main road as cutted arc reduces, and the commutation amounts of processors during the shortest path calculation process reduce. By using the shortest path calculation method of deque, the calculation speed of shortest path obviously increases. Through the new calculation method, the calculation time of 4 million shortest paths in Changsha City is 46 s, the calculation time of 11.7 million shortest paths in Changchun City is 72 s, and both of them satisfy the demand that central guidance path optimization time should be less than 5 rain.
- traffic control /
- central guidance /
- shortest path /
- multi-level network decomposition /
- deque algorithm /
- traveler preference

HTML全文

图 1 计算流程

Figure 1. Calculation flow

下载: 全尺寸图片幻灯片

图 2 查询示例

Figure 2. Query example

下载: 全尺寸图片幻灯片

图 3 多级网络分解过程

Figure 3. Decomposition process of multi-level network

下载: 全尺寸图片幻灯片

图 4 边界节点的移动互换

Figure 4. Moving and exchanging of boundary nodes

下载: 全尺寸图片幻灯片

图 5 双队列数据结构

Figure 5. Two-queue data structure

下载: 全尺寸图片幻灯片

图 6 边界节点信息交互

Figure 6. Information interaction of boundary nodes

下载: 全尺寸图片幻灯片

图 7 长沙市路网节点和弧的分布情况

Figure 7. Distributions of nodes and arcs for road network in Changsha City

下载: 全尺寸图片幻灯片

图 8 长春市路网节点和弧的分布情况

Figure 8. Distributions of nodes and arcs for road network in Changchun City

下载: 全尺寸图片幻灯片

图 9 被切割弧权重之和

Figure 9. Sum of wetights for cutted arcs

下载: 全尺寸图片幻灯片

图 10 运行效率

Figure 10. Operation efficiencies

下载: 全尺寸图片幻灯片

图 11 长沙市优化结果对比

Figure 11. Comparison of optimization results in Changsha City

下载: 全尺寸图片幻灯片

图 12 长春市优化结果对比

Figure 12. Comparison of optimization results in Changchun City

下载: 全尺寸图片幻灯片

表 1 数据库存储

Table 1. Database storage

下载: 导出CSV

表 2 路网特征

Table 2. Network characteristics

下载: 导出CSV

表 3 普通PC机群测试结果

Table 3. Test results of ordinary PC cluster

下载: 导出CSV

表 4 联想服务器机群测试结果

Table 4. Test results of Lenovo server cluster

下载: 导出CSV

表 5 惠普工作站机群测试结果

Table 5. Test results of HP workstation cluster

下载: 导出CSV

参考文献(15)

[1]	TOMKEWITSCH R V. Dynamic route guidance and interactive transport management with ALI-SCOUT[J]. IEEE Transactions on Vehicular Technology, 1991, 40(1): 45-50. doi: 10.1109/25.69971
[2]	张赫, 杨兆升, 王伟. 基于实时交通流信息的中心式动态路径诱导系统行车路线优化技术研究[J]. 公路交通科技, 2004, 21(9): 91-94. doi: 10.3969/j.issn.1002-0268.2004.09.024 ZHANG He, YANG Zhao-sheng, WANG Wei. Research on vehicle route optimization of centrally dynamic route guidance systems based on real-time traffic flow information[J]. Journal of Highway and Transportation Research and Development, 2004, 21(9): 91-94. (in Chinese) doi: 10.3969/j.issn.1002-0268.2004.09.024
[3]	DEO N, PANG Chi-yin. Shortest path algorithms: taxonomy and annotation[J]. Networks, 1984, 14(2): 275-323. doi: 10.1002/net.3230140208
[4]	O'CEARBHAILL E A, O'MAHONY M. Parallel implementation of a transportation network model[J]. Journal of Parallel and Distributed Computing, 2005, 65(1): 1-14. doi: 10.1016/j.jpdc.2004.07.003
[5]	王媛. 大范围战略交通协调控制系统关键技术研究[D]. 长春: 吉林大学, 2009. WANG Yuan. Research on key technologies of large-scale strategic traffic coordination and control system[D]. Changchun: Jilin University, 2009. (in Chinese)
[6]	李丽丽. 基于拓扑关系的导航电子地图增量更新关键技术研究[D]. 长春: 吉林大学, 2009. LI Li-li. Key technology research of incremental updating of electronic navigation map based on topological relationship[D]. Changchun: Jilin University, 2009. (in Chinese)
[7]	陈洁, 陆锋. 一种基于双端队列的交通网络最短路径Pallottino优化算法[J]. 中国图象图形学报, 2006, 11(3): 419-424. doi: 10.3969/j.issn.1006-8961.2006.03.019 CHEN Jie, LU Feng. An optimization algorithm of Pallottino implemented with two queues in transportation network[J]. Journal of Image and Graphics, 2006, 11(3): 419-424. (in Chinese) doi: 10.3969/j.issn.1006-8961.2006.03.019
[8]	SUNDELL H, TSIGAS P. Lock-free deques and doubly linked lists[J]. Journal of Parallel and Distributed Computing, 2008, 68(7): 1008-1020. doi: 10.1016/j.jpdc.2008.03.001
[9]	MEYERHENKE H, MONIEN B, SAUERWALD T. A new diffusion-based multilevel algorithm for computing graph partitions[J]. Journal of Parallel and Distributed Computing, 2009, 69(9): 750-761. doi: 10.1016/j.jpdc.2009.04.005
[10]	KARYPIS G, KUMAR V. Multilevel k-way partitioning scheme for irregular graphs[J]. Journal of Parallel and Distributed Computing, 1998, 58(1): 96-129.
[11]	ZHAN F B, NOON C E. Shortest path algorithms: an evaluation using real road networks[J]. Transportation Science, 1998, 32(1): 65-73. doi: 10.1287/trsc.32.1.65
[12]	ZHAN F B. Three fastest shortest path algorithms on real road networks: data structures and procedures[J]. Journal of Geographic Information and Decision Analysis, 1997, 1(1): 70-82.
[13]	MEYER U. Design and analysis of sequential and parallel single-source shortest-paths algorithms[D]. Saarbrücken: Universität des Saarlandes, 2002.
[14]	MEYER U, SANDERS P. Δ-stepping: aparallelizable shortest path algorithm[J]. Journal of Algorithms, 2003, 49(1): 114-152.
[15]	KARYPIS G, KUMAR V. Multilevel k-way hypergraph partitioning[J]. VLSI Design, 2000, 11(3): 343-348