Optimal velocity difference model of non-neighboring vehicles
Article Text (Baidu Translation)
-
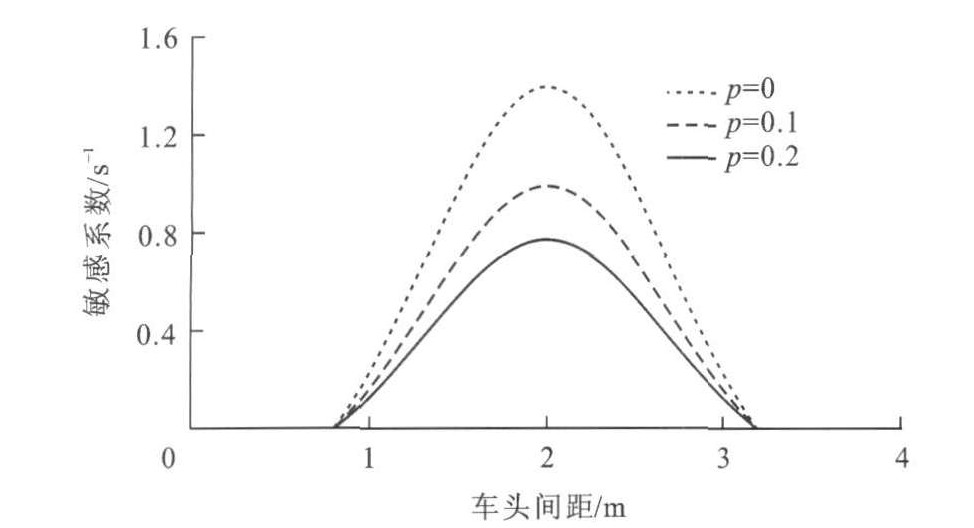
摘要: 描述了优化速度模型、广义力模型和全速度差模型, 分析了这些模型解决交通流问题的不足。在全速度差模型的基础上, 考虑驾驶人对非邻近双前车优化速度差信息的关注程度, 提出了最优速度差模型。通过线性稳定性分析, 得到交通流的稳定性条件, 通过数值模拟, 比较了最优速度差模型与全速度差模型。模拟结果表明: 应用最优速度差模型, 临界稳定性曲线的敏感系数变小, 自由流区域明显增大; 当敏感系数为0.310 0s-1时, 交通流稳定性增强, 并未出现负速度现象; 当敏感系数为0.777 8s-1且反应系数为0.2时, 车辆速度基本保持在0.963 5m·s-1; 随着反应系数的增大, 速度迟滞环逐渐趋向于一点。可见, 最优速度差模型有效。Abstract: The optimal velocity model, generalized force model and full velocity difference model were described, and the deficiencies of these models solving traffic flow problem were analyzed.On the basis of full velocity difference model, the concern degree of driver on the optimial velocity difference information of two non-neighboring preceding vehicles was considered, and the optimal velocity difference model was put out.Through linear stability analysis, the stability condition of traffic flow was obtained.By using numerical simulation, optimal velocity difference model and full velocity difference model were compared.Simulation result shows that by using optimal velocity difference model, the sensitive coefficient of critical stability curve becomes smaller, free flow region increases obviously.While sensitive coefficient is 0.310 0 s-1, traffic flow stability strengthens, and the phenomenon of negative velocity does not appear.While sensitive coefficient is 0.777 8 s-1, and reaction coefficient is 0.2, vehicle velocities can basically maintain 0.963 5 m·s-1.With the increase of reaction coefficient, the produce hysteresis loops of velocities gradually tend to a point.So the optimal velocity difference model is effective.
-
图 2 a为0.310 0 s-1, t为100 s时的车辆速度分布
Figure 2. Vehicle velocity distributions while a is 0.310 0 s-1 and t is 100 s
图 3 a为0.310 0 s-1, t为400 s时的车辆速度分布
Figure 3. Vehicle velocity distributions while a is 0.310 0 s-1 and t is 400 s
图 4 a为0.777 8 s-1, t为100 s时的车辆速度分布
Figure 4. Vehicle velocity distributions while a is 0.777 8 s-1 and t is 100 s
图 5 a为0.777 8 s-1, t为400 s时的车辆速度分布
Figure 5. Vehicle velocity distributions while a is 0.777 8 s-1 and t is 400 s
-
[1] 贾宁, 马寿峰. 考虑摩擦干扰的机非混合交通流元胞自动机仿真[J]. 系统仿真学报, 2011, 23(2): 390-394. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ201102036.htmJIA Ning, MA Shou-feng. Simulation of mixed traffic flow with friction interference using cellular automata[J]. Journal of System Simulation, 2011, 23(2): 390-394. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ201102036.htm [2] 钱勇生, 曾俊伟, 杜加伟, 等. 考虑意外事件对交通流影响的元胞自动机交通流模型[J]. 物理学报, 2011, 60(6): 103-112. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201106018.htmQIAN Yong-sheng, ZENG Jun-wei, DU Jia-wei, et al. Cellular automaton traffic flow model considering influence of accidents[J]. Acta Physica Sinica, 2011, 60(6): 103-112. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201106018.htm [3] BANDO M, HASEBE K, NAKAYAMA A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035-1042. doi: 10.1103/PhysRevE.51.1035 [4] CHRISTOPH W. Asymptotic solutions for a multi-anticipative car-following model[J]. Physica A, 1998, 260(4): 218-224. [5] ZHU Hui-bing, DAI Shi-qiang. Analysis of car-following model considering driver's physical delay in sensing headway[J]. Physica A, 2008, 387(13): 3290-3298. doi: 10.1016/j.physa.2008.01.103 [6] SIPAHI R, NICULESCU S I. Stability of car following with human memory effects and automatic headway compensation[J]. Philosophical Transactions of Royal Society, 2010, 368(1928): 4563-4583. [7] 孙棣华, 李永福, 田川. 基于多前车位置及速度差信息的车辆跟驰模型[J]. 系统工程理论与实践, 2010, 30(7): 1326-1332. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL201007027.htmSUN Di-hua, LI Yong-fu, TIAN Chuan. Car-following model based on the information of multiple ahead and velocity difference[J]. Systems Engineering—Theory and Practice, 2010, 30(7): 1326-1332. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL201007027.htm [8] HELBING D, TILCH B. Generalized force model of traffic dynamics[J]. Physical Review E, 1998, 58(1): 133-138. doi: 10.1103/PhysRevE.58.133 [9] JIANG Rui, WU Qing-song, ZHU Zuo-jin. Full velocity difference model for a car following theory[J]. Physical Review E, 2001, 64(1): 63-66. [10] 王涛, 高自友, 赵小梅. 多速度差模型及稳定性分析[J]. 物理学报, 2006, 55(2): 634-640. doi: 10.3321/j.issn:1000-3290.2006.02.028WANG Tao, GAO Zi-you, ZHAO Xiao-mei. Multiple velocity difference model and its stability analysis[J]. Acta Physica Sinica, 2006, 55(2): 634-640. (in Chinese) doi: 10.3321/j.issn:1000-3290.2006.02.028 [11] 彭光含, 孙棣华, 何恒攀. 交通流双车跟驰模型与数值仿真[J]. 物理学报, 2008, 57(12): 7541-7546. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200812023.htmPENG Guang-han, SUN Di-hua, HE Heng-pan. Two-car following model of traffic flow and numerical simulation[J]. Acta Physica Sinica, 2008, 57(12): 7541-7546. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200812023.htm [12] 彭光含. 交通流复杂耦合动态特性模拟研究[D]. 重庆: 重庆大学, 2009.PENG Guang-han. Simulation research on complicated coupling dynamical characteristics of traffic flow[D]. Chongqing: Chongqing University, 2009. (in Chinese) [13] TIAN Jun-fang, JIA Bin, LI Xin-gang, et al. A new car-following model considering velocity anticipation[J]. Chinese Physics B, 2010, 19(1): 197-203. [14] TREIBER M, HENNECHE A, HELBING D. Derivation, properties, and simulation of a gas-kinetic-based, nonlocal traffic model[J]. Physical Review E, 1999, 59(1): 239-253. -
下载:
点击查看大图
图(6)
计量
- 文章访问数: 878
- HTML全文浏览量: 170
- PDF下载量: 767
- 被引次数: 0
