0. Introduction

Loess covers plenty of areas in Northwest China and North China and often is unsaturated.The strength property of unsaturated loess is complicated, and is an urgent and difficult problem^[1]in slope, subgrade and tunnel design.Many scholars studied the strength of unsaturated soil.In general, the measurement of suction is conducted through sensitive ceramic plate or ceramic tube element^[2-7], the balance of water-air interface lasts over one week, therefore, one complete laboratory experiment on unsaturated soil's strength needs over one month, so that a lot of researches on unsaturated soil are still conducted in laboratory.So in this paper, the suction's contribution to the strength of soil is regarded as the increment of minor principal stress or confining pressure, through getting the increment, a function of the strength of unsaturated loess respecting to the increments of strength indexes is gotten, and the relationship between the strength and water content of unsaturated soil is set up to predict and analyse the strength of unsaturated soil.

1. Calculation method of strength of unsaturated loess

There are some air and water in the pores of unsaturated soil.The difference between pore air pressure U_a and pore water pressure U_w is called suction U_a -U_w. Many test results demonstrate that the suction makes the strength of unsaturated soil increase, the larger the suction is, the larger the shear strength of unsaturated soil is.

In the analysis of the strength of unsaturated soil, the suction's contribution to the strength as confining pressure is considered.Referencing to previous results on reinforced soil^[8-9], the funtion on the ultimate strength of unsaturated soil is gotten while the angle of internal friction and the cohesion increase, and the derivation for the funtion is just as following.

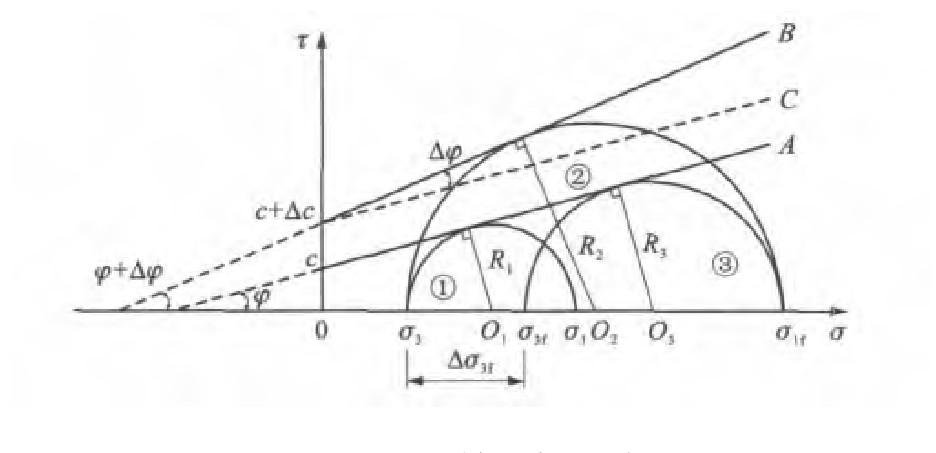
The failure envelope is a straight line, in which, its inclination is φ+Δφ, its intercept is c+Δc, φ is the angle of internal friction, Δφ is the increment of angle of internal friction, c is the cohesion, Δc is the increment of cohesion, and their relationship is shown in Fig. 1.

Figure  1.  Variable relationship

DownLoad: Full-Size Img PowerPoint

In Fig. 1, τ is shear stress, σ is normal stress, and O₁-O₃ are the centers of Mohr's circle 1-3 respectively. Mohr's circle 1 represents no suction, its radius is R₁ , and its failure envelope is straight line A.Mohr's circle 2 represents having suction, its radius is R₂ , its failure envelope is straight line B, and intersects straight line C that parallels to straight line A.The skeleton of unsaturated soil bears major principal stressσ₁ , minor principal stressσ₃ and the increment of confining pressure Δσ_3f due to the suction, so the failure state corresponds to Mohr's circle 3.At this time, actual minor principal stress is σ_3f , the suction provides the additional stress Δσ_3f=σ_3f -σ₃ to the skeleton.The radius of circle 3 is R₃ , andσ_1f is the major principal stress at failure.From Fig. 1

For circle 3

For circle 2

Which leads to

Δσ_3f is obtained by substituting Eq.(2)and Eq.(3)into Eq.(1)

The limit equilibrium equation for soil is just as following

σ₁ is obtained by substituting Eq.(4)into the limit equilibrium equation

Simplifying Eq.(5), it is obtained

in which

From Eq.(6), Δφ makes the generalized confining pressure σ₃ increase, and both Δφ and Δc make the generalized cohesion c increase.

2. Comparison of calculation result and test result

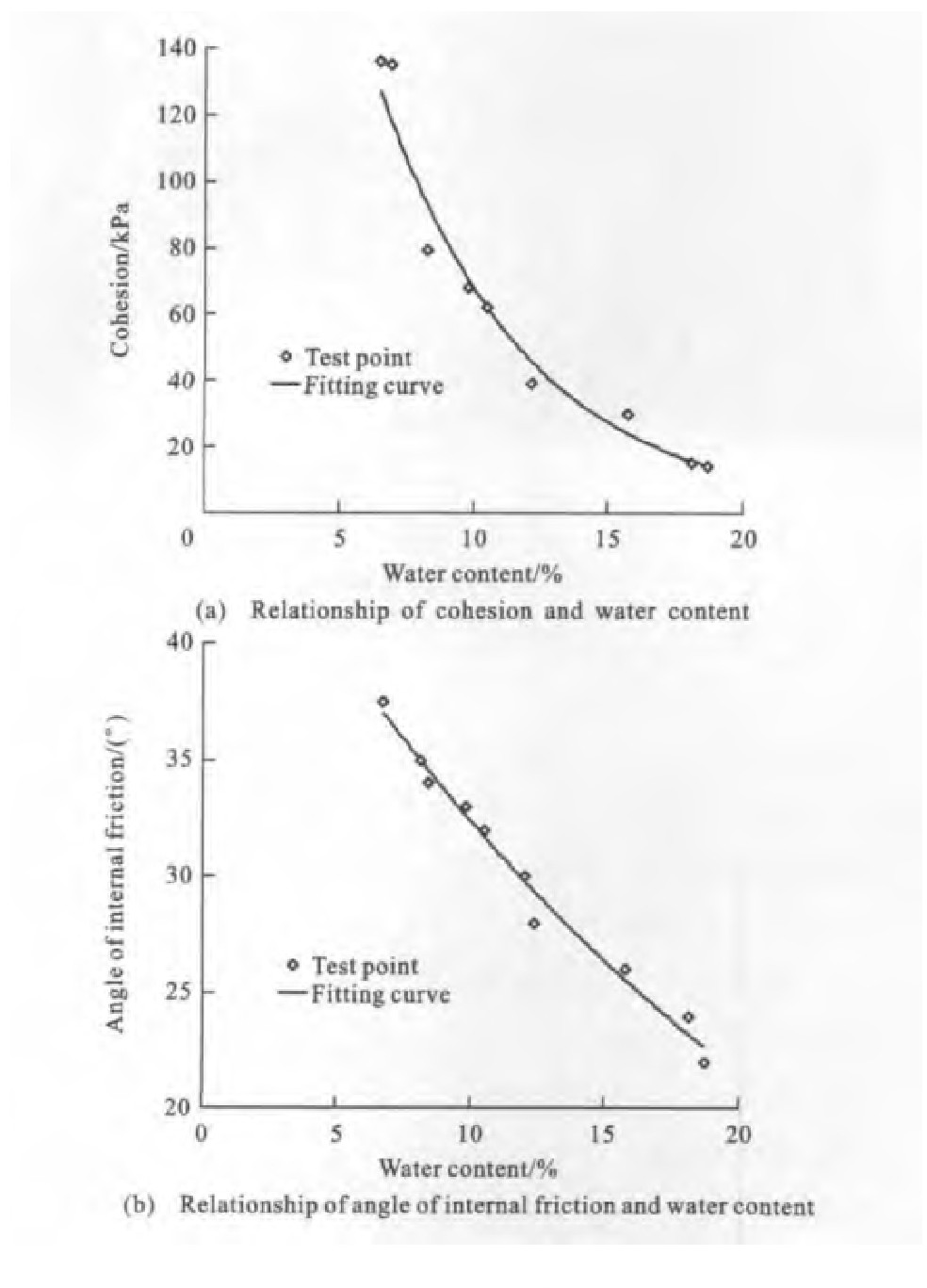
Because measuring the suction is very difficult, a plenty of researches on the strength of unsaturated soil are focused on the train of thought of water content-suction-shear strength.With the increase of water content, the suction decreases, and the suction is related to the shear strength closely^[10].Making use of the data from the triaxial tests on unsaturated loess^[11-12], the relationships of the cohesion and the angle of internal friction with water content are obtained by using the leastsquare method, and are shown in Fig. 2 and Tab. 1.In Tab. 1, w is water content, and Δw is its increment.

Figure  2.  Relationship of strength indexes and water content

DownLoad: Full-Size Img PowerPoint

Table  1.  Relationship of strength indexes and water content

 | Show Table

DownLoad: CSV

From Fig. 2, the cohesion and the angle of internal friction of unsaturated loess decrease with the increase of water content exponentially.If the confining pressure is constant, the larger soil specimen bears axial load, the larger the shear strength of soil specimen is.Substituting the formula between the strength indexes and water content into Eq.(5), the curves of major principal stress and water content are obtained and shown in Fig. 3.

Figure  3.  Relationship curves of major principal stress and water content under different σ₃

DownLoad: Full-Size Img PowerPoint

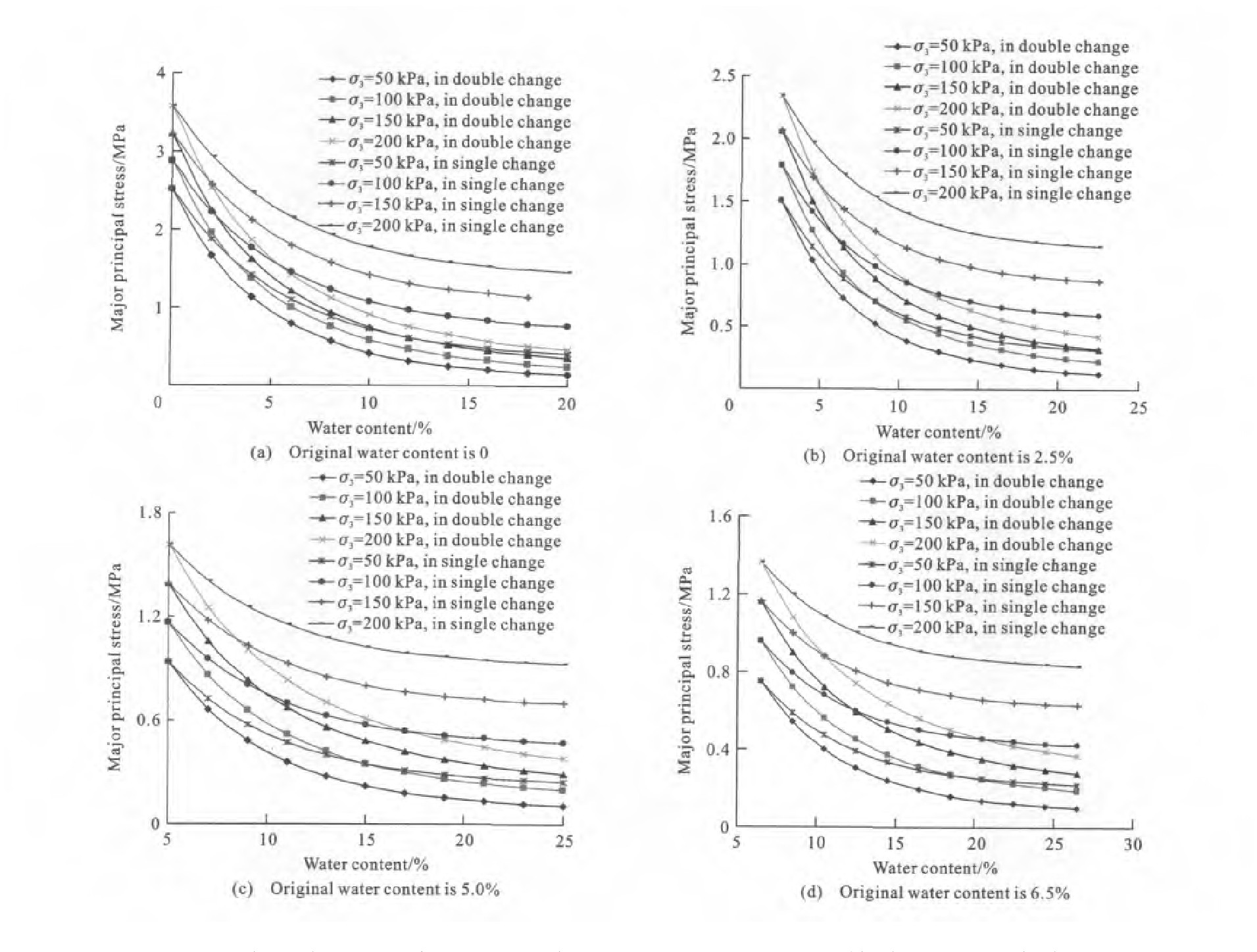
From Fig. 3, the calculation values and test values of major principa stresses decrease with the increase of water content, and their differences become less with the increase of water content.When original water content is 6.9%, the confining pressure is 50kPa, the maximum relative error is 11.63%.When water content is 6.9%, the minimum relative error is 1.59%.When water content reaches 18.1%, the calculation data are consistent with experimental data.Original water content does not affect the calculation result of major principa stress, which shows that Eq.(5)is appropriate to describe the the strength of unsaturated soil.Using Eq.(5)and Fig. 2, the strengths of unsaturated soil for different water contents can be predicted.

When the cohesion and the angle of internal friction change with water content, and only the cohesion changes with water content, the major principal stresses are calculated by using Eq.(5), and shown in Fig. 4.The major principal stresses calculated in double change are less than that in single change.For a given water content, the difference of major principal stresses in two kinds situations becomes larger with the increase of water content, becomes less with the increase of confining pressure.When original water content is constant, the major principal stress in single change is 2.26to 3.17times more than that in double change, which illustrates that a little change for the cohesion and the angle of internal friction can causes larger change of strength of unsaturated soil, which confirms that Eq.(5)is right for predicting the strength of unsaturated soil.

Figure  4.  Relationship curves of major principal stress and water content in double change and single change

DownLoad: Full-Size Img PowerPoint

3. Conclusion

In this paper, the function of the change of major principal stress with the strength index increments of loess is put forward, the curves of strength indexes-water content are analyzed, the major principal stresses in failure state for different water contents are calculated, and the calculation data coincide with the experiment data well.The major principal stress calculated in single change is larger than that in double change, and their difference becomes larger with the increase of water content.